【数据结构】并查集

一、并查集原理

在一些应用问题中，需要将 n 个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-find set)。

例如有 10 个数字如下，开始时每个元素单独成为一个集体，所以我们可以使用数组模拟，用数组下标标记不同的元素，内容如果是 -1 表示自己单独是一个集合，并且只有自己一个元素；如果是负几，就代表这个集合有几个元素；如果是大于0，代表自己是一个集合的元素，该集合的数组下标就是这个大于0的数：

我们简单对这些数进行分组：

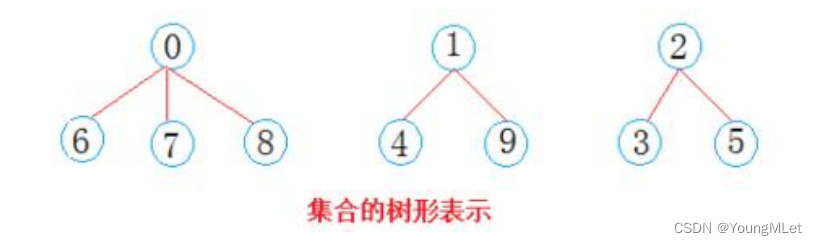
用数组表示如下：

所以总结一下：

1. 数组的下标对应集合中元素的编号
2. 数组中如果为负数，负号代表根，数字代表该集合中元素个数
3. 数组中如果为非负数，代表该元素双亲在数组中的下标

假设我们将 1 下标的集合合并到 0 下标中，结果如下：

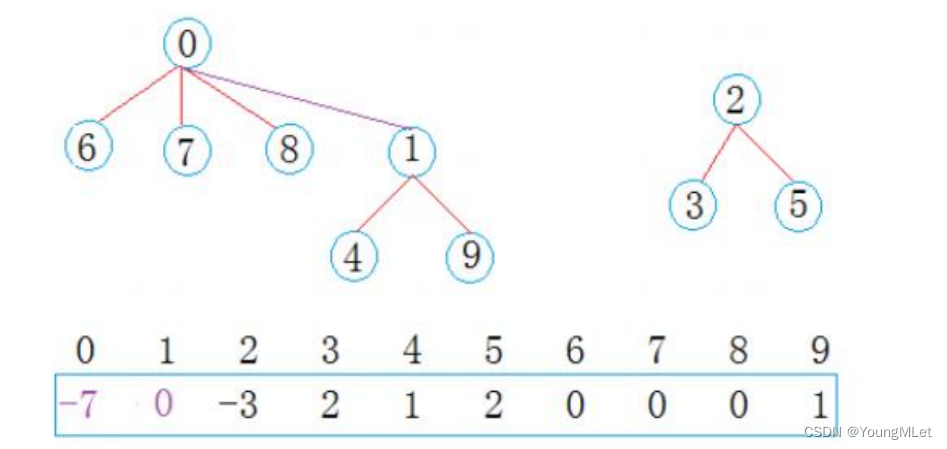
现在 0 下标的集合有 7 个元素， 2 下标的集合有3个人，总共两个集合。

通过以上例子可知，并查集一般可以解决以下问题：

1. 查找元素属于哪个集合

• 沿着数组表示树形关系以上一直找到根(即：树中元素为负数的位置)

2. 查看两个元素是否属于同一个集合

• 沿着数组表示的树形关系往上一直找到树的根，如果根相同表明在同一个集合，否则不在

3. 将两个集合归并成一个集合

• 将两个集合中的元素合并
• 将一个集合名称改成另一个集合的名称

4. 集合的个数

• 遍历数组，数组中元素为负数的个数即为集合的个数。

二、并查集简单实现

并查集的基本实现如下代码所示：

				class UnionFind
				{
				public:
				    // 构造函数初始化数组
				    UnionFind(size_t size) 
				        :_uf(size, -1)
				    {}
				
				    // 找到根的下标
				    int FindRoot(int index)
				    {
				        while(_uf[index] >= 0){
				            index = _uf[index];
				        }
				        return index;
				    }
				
				    // 合并两个集合
				    bool Union(int index1, int index2)
				    {
				        int root1 = FindRoot(index1);
				        int root2 = FindRoot(index2);
				
				        // 已经在一个集合中
				        if(root1 == root2) return false;
				
				        _uf[root1] += _uf[root2];
				        _uf[root2] = root1;
				
				        return true;
				    }
				
				    // 返回集合的数量
				    size_t Count() const 
				    {
				        size_t cnt = 0;
				        for(auto e : _uf){
				            if(e < 0){
				                cnt++;
				            }
				        }
				        return cnt;
				    }
				
				private:
				    std::vector<int> _uf;
				};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

三、并查集的应用

下面我们看两道题对于并查集的应用：

1. 省份数量

Leetcode -547. 省份数量

题目：有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中省份的数量。

示例一：

输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

示例二：

输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

提示：

• 1 <= n <= 200
• n == isConnected.length
• n == isConnected[i].length
• isConnected[i][j] 为 1 或 0
• isConnected[i][i] == 1
• isConnected[i][j] == isConnected[j][i]

思路：我们只需要遍历这个二维数组，只要是值为1的位置，我们就将这个位置的下标放入一个集合中，我们同样使用数组模拟并查集，最后统计并查集中小于0的个数即是省份的数量。代码如下：

				class Solution {
				public:
				    int findCircleNum(vector<vector<int>>& isConnected) {
				        vector<int> uf(isConnected.size(), -1);
				
				        auto FindRoot = [&uf](int index)
				        {
				            while(uf[index] >= 0){
				                index = uf[index];
				            }
				            return index;
				        };
				
				        for(int i = 0; i < isConnected.size(); i++){
				            for(int j = i + 1; j < isConnected[i].size(); j++){
				                if(isConnected[i][j] == 1){
				                    int root1 = FindRoot(i);
				                    int root2 = FindRoot(j);
				                    if(root1 != root2){
				                        uf[root1] += uf[root2];
				                        uf[root2] = root1;
				                    }
				                }
				            }
				        }
				        int cnt = 0;
				        for(auto e : uf){
				            if(e < 0){
				                cnt++;
				            }
				        }
				        return cnt;
				    }
				};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

2. 等式方程的可满足性

Leetcode -990. 等式方程的可满足性

题目：给定一个由表示变量之间关系的字符串方程组成的数组，每个字符串方程 equations[i] 的长度为 4，并采用两种不同的形式之一：“a==b” 或 “a!=b”。在这里，a 和 b 是小写字母（不一定不同），表示单字母变量名。

只有当可以将整数分配给变量名，以便满足所有给定的方程时才返回 true，否则返回 false。

示例 1：
输入：[“a==b”,“b!=a”]
输出：false
解释：如果我们指定，a = 1 且 b = 1，那么可以满足第一个方程，但无法满足第二个方程。没有办法分配变量同时满足这两个方程。

示例 2：
输入：[“ba","ab”]
输出：true
解释：我们可以指定 a = 1 且 b = 1 以满足满足这两个方程。

示例 3：
输入：[“ab","bc”,“a==c”]
输出：true

示例 4：
输入：[“ab",“b!=c”,"ca”]
输出：false

示例 5：
输入：[“cc","bd”,“x!=z”]
输出：true

提示：

• 1 <= equations.length <= 500
• equations[i].length == 4
• equations[i][0] 和 equations[i][3] 是小写字母
• equations[i][1] 要么是 ‘=’，要么是 ‘!’
• equations[i][2] 是 ‘=’

思路：因为只是对小写字母之间判断是否有相悖的结论，所以我们可以先遍历一遍，将所有相等的放入一个并查集中；然后第二次遍历就找不相等的，如果这两个不相等的元素出现在并查集中，说明结论相悖，直接返回 false；否则返回 true；代码如下：

				class Solution {
				public:
				    bool equationsPossible(vector<string>& equations) 
				    {
				        vector<int> uf(26, -1);
				        
				        auto FindRoot = [&uf](int index)
				        {
				            while(uf[index] >= 0){
				                index = uf[index];
				            }
				            return index;
				        };
						
						// 先将相同的元素放入一个集合
				        for(auto& str : equations){
				            int root1 = FindRoot(str[0] - 'a');
				            int root2 = FindRoot(str[3] - 'a');
				
				            if(str[1] == '='){
				                if(root1 != root2){
				                    uf[root1] += uf[root2];
				                    uf[root2] = root1;
				                }
				            }
				        }
				
				        for(auto& str : equations){
				            int root1 = FindRoot(str[0] - 'a');
				            int root2 = FindRoot(str[3] - 'a');
							
							// 相悖
				            if(str[1] == '!'){
				                if(root1 == root2){
				                    return false;
				                }
				            }
				        }
				        return true;
				    }
				};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41