- 1Android面试题--HashMap原理分析_android hashmap原理
- 2pmon常用操作_pmon查看有哪些网卡
- 3谷歌公司推荐的计算机科学在线课程&学习路线_计算机国外课程学习路线
- 4技术中台的作用是什么,在什么情况下才有必要做技术中台?
- 5链表篇-链表翻转
- 6什么是红黑树?这篇讲解很全面!
- 7HTTP请求时connectionRequestTimeout 、connectionTimeout、socketTimeout三个超时时间的含义
- 8数据结构小记【Python/C++版】——链表篇
- 9驻极体式MIC电路设计_驻极体麦 差分电路
- 10java线程变量那点事儿_java 定义的变量线程也能用
数据结构—图—最小生成树_数据结构最小生成树
赞
踩
什么是最小生成树
一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。 [1] 最小生成树可以用kruskal(克鲁斯卡尔)算法或prim(普里姆)算法求出。

2、普里姆算法—Prim算法
算法思路:
首先就是从图中的一个起点a开始,把a加入U集合,然后,寻找从与a有关联的边中,权重最小的那条边并且该边的终点b在顶点集合:(V-U)中,我们也把b加入到集合U中,并且输出边(a,b)的信息,这样我们的集合U就有:{a,b},然后,我们寻找与a关联和b关联的边中,权重最小的那条边并且该边的终点在集合:(V-U)中,我们把c加入到集合U中,并且输出对应的那条边的信息,这样我们的集合U就有:{a,b,c}这三个元素了,一次类推,直到所有顶点都加入到了集合U。
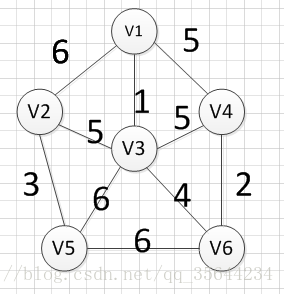
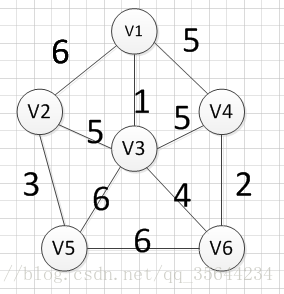
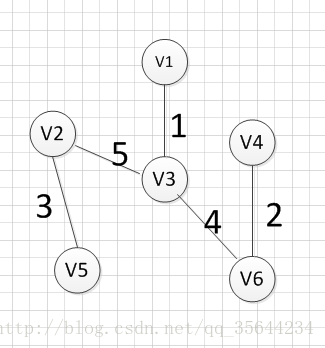
下面我们对下面这幅图求其最小生成树:
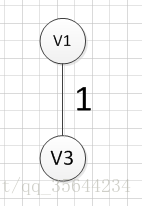
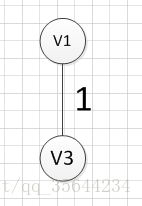
假设我们从顶点v1开始,所以我们可以发现(v1,v3)边的权重最小,所以第一个输出的边就是:v1—v3=1:
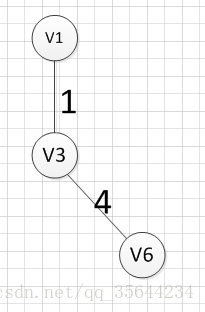
然后,我们要从v1和v3作为起点的边中寻找权重最小的边,首先了(v1,v3)已经访问过了,所以我们从其他边中寻找,发现(v3,v6)这条边最小,所以输出边就是:v3—v6=4
然后,我们要从v1、v3、v6这三个点相关联的边中寻找一条权重最小的边,我们可以发现边(v6,v4)权重最小,所以输出边就是:v6—v4=2.
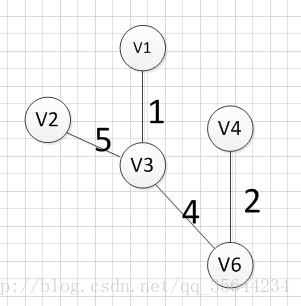
然后,我们就从v1、v3、v6、v4这四个顶点相关联的边中寻找权重最小的边,发现边(v3,v2)的权重最小,所以输出边:v3—–v2=5
然后,我们就从v1、v3、v6、v4,v2这2五个顶点相关联的边中寻找权重最小的边,发现边(v2,v5)的权重最小,所以输出边:v2—–v5=3
最后,我们发现六个点都已经加入到集合U了,我们的最小生成树建立完成。
时间复杂度
| 最小边、权的数据结构 | 时间复杂度(总计) |
|---|---|
| 邻接矩阵、搜索 | O(N^2) |
| 二叉堆(后文伪代码中使用的数据结构)、邻接表 | O((N + E) log(N)) = O(E log(N)) |
| 斐波那契堆、邻接表 | O(E + N log(N)) |
通过邻接矩阵图表示的简易实现中,找到所有最小权边共需O(V)的运行时间。使用简单的二叉堆与邻接表来表示的话,普里姆算法的运行时间则可缩减为O(ElogV),其中E为连通图的边数,V为顶点数。如果使用较为复杂的斐波那契堆,则可将运行时间进一步缩短为O(E+VlogV),这在连通图足够密集时(当E满足Ω(VlogV)条件时),可较显著地提高运行速度。
代码实现:
- #define MAXN 1000
- #define INF 1<<30
- int closest[MAXN],lowcost[MAXN],m;//m为节点的个数
- int G[MAXN][MAXN];//邻接矩阵
- int prim()
- {
- for(int i=0; i<m; i++)
- {
- lowcost[i]=INF;
- }
- for(int i=0; i<m; i++)
- {
- closest[i]=0;
- }
- closest[0]=-1;//加入第一个点,-1表示该点在集合U中,否则在集合V中
- int num=0,ans=0,e=0;//e为最新加入集合的点
- while(num<m-1)//加入m-1条边
- {
- int micost=INF,miedge=-1;
- for(int i=0; i<m; i++)
- if(closest[i]!=-1)
- {
- int temp=G[e][i];
- if(temp<lowcost[i])
- {
- lowcost[i]=temp;
- closest[i]=e;
- }
- if(lowcost[i]<micost)
- micost=lowcost[miedge=i];
- }
- ans+=micost;
- closest[e=miedge]=-1;
- num++;
- }
- return ans;
- }

Kruskal—克鲁斯卡算法
算法思路:
(1)将图中的所有边都去掉。
(2)将边按权值从小到大的顺序添加到图中,保证添加的过程中不会形成环
(3)重复上一步直到连接所有顶点,此时就生成了最小生成树。这是一种贪心策略。
这里同样我们给出一个和Prim算法讲解中同样的例子,模拟克鲁斯卡算法生成最小生成树的详细的过程:
首先完整的图如下图:
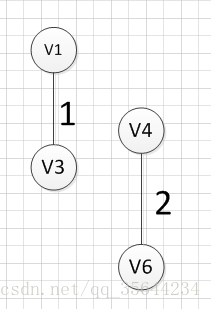
然后,我们需要从这些边中找出权重最小的那条边,可以发现边(v1,v3)这条边的权重是最小的,所以我们输出边:v1—-v3=1
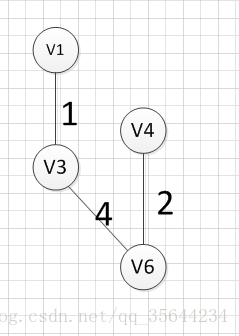
然后,我们需要在剩余的边中,再次寻找一条权重最小的边,可以发现边(v4,v6)这条边的权重最小,所以输出边:v4—v6=2
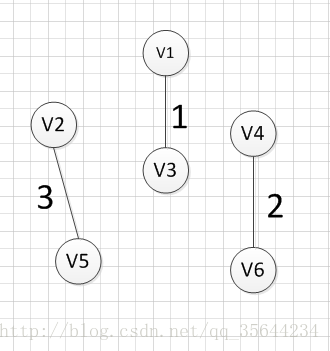
然后,我们再次从剩余边中寻找权重最小的边,发现边(v2,v5)的权重最小,所以可以输出边:v2—v5=3,
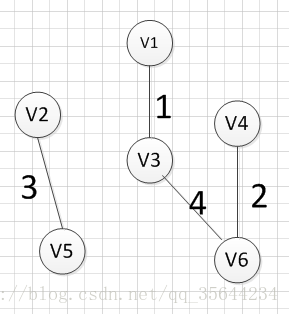
然后,我们使用同样的方式找出了权重最小的边:(v3,v6),所以我们输出边:v3—v6=4
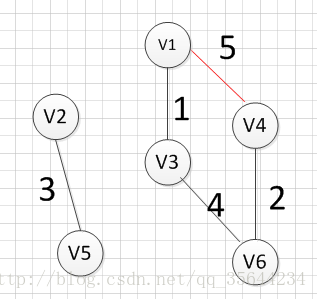
好了,现在我们还需要找出最后一条边就可以构造出一颗最小生成树,但是这个时候我们有三个选择:(v1,V4),(v2,v3),(v3,v4),这三条边的权重都是5,首先我们如果选(v1,v4)的话,得到的图如下:
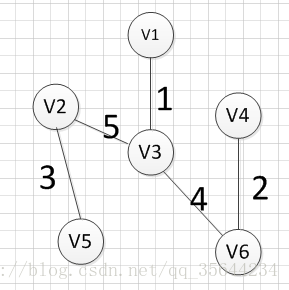
我们发现,这肯定是不符合我们算法要求的,因为它出现了一个环,所以我们再使用第二个(v2,v3)试试,得到图形如下:
我们发现,这个图中没有环出现,而且把所有的顶点都加入到了这颗树上了,所以(v2,v3)就是我们所需要的边,所以最后一个输出的边就是:v2—v3=5
- #include<iostream>
- #include<queue>
- using namespace std;
- struct EdgeNode
- {
- int v1;
- int v2;
- int value;
- bool operator<(const EdgeNode &a) const
- {
- return a.value<value;
- }
- };
- int *root;
- priority_queue<EdgeNode> pq;
- int Find(int x)
- {
- int i=x;
- while(i!=root[i])
- i=root[i];
- while(i!=root[x])
- {
- temp=root[x];
- root[x]=i;
- x = temp;
- }
- return i;
- }
- void Union(int a,int b)
- {
- a=Find(a);
- b=Find(b);
- if(a!=b)
- root[a]=b;
- }
- void Kruskal()
- {
- EdgeNode b;
- cout<<"加入最小生成树中的边依次为: "<<endl;
- while(!pq.empty())
- {
- b=pq.top();
- pq.pop();
- if(Find(b.v1)!=Find(b.v2))
- {
- cout<<b.v1<<"----"<<b.v2<<endl;
- Union(b.v1,b.v2);
- }
- }
- }
- void main()
- {
- int n=0;
- int m=0;
- cout<<"请输入图中点的个数: "<<endl;
- cin>>n;
- root=new int [n+1];
- for(int i=1; i<=n; i++)
- root[i]=i;
- cout<<"请输入图中边的条数: "<<endl;
- cin>>m;
- EdgeNode a;
- cout<<"请依次输入每条边的两个顶点及其权重: "<<endl;
- while(m--)
- {
- cin>>a.v1>>a.v2>>a.value;
- pq.push(a);
- }
- Kruskal();
- }