【数据结构】链式二叉树的创建

binaryTreeNode.h

#pragma once
#include<iostream>
template<class T>
struct binaryTreeNode
{
	T element;
	binaryTreeNode<T>* leftChild, * rightChild;
	binaryTreeNode() {}
	binaryTreeNode(const T& element, binaryTreeNode<T>* leftChild = NULL,
		binaryTreeNode<T>* rightChild = NULL) {
		this->element = element;
		this->leftChild = leftChild;
		this->rightChild = rightChild;
	}
};


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

linkedBinaryTree.h

#ifndef linkedBinaryTree_
#define linkedBinaryTree_
#include"binaryTreeNode.h"
#include<queue>
#include<iostream>
using namespace std;
template<class T>
class linkedBinaryTree
{
public:
	linkedBinaryTree();
	~linkedBinaryTree();
	bool empty()const;
	int size()const;
	binaryTreeNode<T>* createBinaryTree(binaryTreeNode<T>* t);
	void createBinaryTree();
	int height_recursion(binaryTreeNode<T>* t);//递归求高度
	int height_level();//层次遍历求高度
	int height();
	void preOrder(void (*theVisit)(binaryTreeNode<T>*));
	void inOrder(void (*theVisit)(binaryTreeNode<T>*));
	void postOrder(void (*theVisit)(binaryTreeNode<T>*));
	void levelOrder(void(*theVisit)(binaryTreeNode<T>*));
	void preOrderOutput();
	void inOrderOutput();
	void postOrderOutput();
	void erase();
private:
	binaryTreeNode<T>* root;
	int treesize;
	static void (*visit)(binaryTreeNode<T>*);
	static void preOrder(binaryTreeNode<T>*);
	static void inOrder(binaryTreeNode<T>*);
	static void postOrder(binaryTreeNode<T>*);
	static void dispose(binaryTreeNode<T>*);
	static void output(binaryTreeNode<T>*);
};
template<class T>
void(*linkedBinaryTree<T>::visit)(binaryTreeNode<T>*) = NULL;
#endif
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

linkedBinaryTree.cpp

#include "linkedBinaryTree.h"
#include<queue>

template<class T>
linkedBinaryTree<T>::linkedBinaryTree()
{
	root = NULL;
	treesize = 0;
}

template<class T>
linkedBinaryTree<T>::~linkedBinaryTree()
{
	erase();
}

template<class T>
bool linkedBinaryTree<T>::empty() const
{
	return treesize == 0;
}

template<class T>
int linkedBinaryTree<T>::size() const
{
	return treesize;
}

template<class T>
binaryTreeNode<T>* linkedBinaryTree<T>::createBinaryTree(binaryTreeNode<T>* t)
{
	T element;
	cin >> element;
	if (element == '#') {
		return NULL;
	}
	else {
		treesize++;
		t = new binaryTreeNode<T>(element);
		t->leftChild = createBinaryTree(t->leftChild);
		t->rightChild = createBinaryTree(t->rightChild);
	}
	return t;
}


template<class T>
void linkedBinaryTree<T>::createBinaryTree()
{
	root = createBinaryTree(root);
}

template<class T>
int linkedBinaryTree<T>::height_recursion(binaryTreeNode<T>* t)
{
	if (t == NULL) {
		return 0;
	}
	int h1 = height_recursion(t->leftChild);
	int h2 = height_recursion(t->rightChild);
	if (h1 > h2) {
		return h1 + 1;
	}
	else {
		return h2 + 1;
	}
}

template<class T>
int linkedBinaryTree<T>::height_level()
{
	queue<binaryTreeNode<T>*> q;
	q.push(root);
	int n = 0,len;
	binaryTreeNode<T>* cur;
	while (!q.empty()) {
		n++;
		len = q.size();
		for (int i = 0; i < len; i++) {
			cur = q.front();
			q.pop();
			if (cur->leftChild != NULL) {
				q.push(cur->leftChild);
			}
			if (cur->rightChild != NULL) {
				q.push(cur->rightChild);
			}
		}
	}
	return n;
}

template<class T>
int linkedBinaryTree<T>::height()
{
	return height_recursion(root);
}

template<class T>
void linkedBinaryTree<T>::preOrder(void(*theVisit)(binaryTreeNode<T>*))
{
	visit = theVisit;
	preOrder(root);
}

template<class T>
void linkedBinaryTree<T>::inOrder(void(*theVisit)(binaryTreeNode<T>*))
{
	visit = theVisit;
	inOrder(root);
}

template<class T>
void linkedBinaryTree<T>::postOrder(void(*theVisit)(binaryTreeNode<T>*))
{
	visit = theVisit;
	postOrder(root);
}

template<class T>
void linkedBinaryTree<T>::levelOrder(void(*theVisit)(binaryTreeNode<T>*))
{
	queue<binaryTreeNode<T>*>q;
	q.push(root);
	while (q != NULL) {
		binaryTreeNode<T>* cur = q.front();
		q.pop();
		theVisit(cur);

		if (cur->leftChild != NULL) {
			q.push(cur->leftChild);
		}
		if (cur->rightChild != NULL) {
			q.push(cur->rightChild);
		}
	}

}

template<class T>
void linkedBinaryTree<T>::preOrderOutput()
{
	preOrder(output);
	cout << "\n";
}

template<class T>
void linkedBinaryTree<T>::inOrderOutput()
{
	inOrder(output);
	cout << "\n";
}

template<class T>
void linkedBinaryTree<T>::postOrderOutput()
{
	postOrder(output);
	cout << "\n";
}

template<class T>
void linkedBinaryTree<T>::erase()
{
	postOrder(dispose);
	root = NULL;
	treesize = 0;
}

template<class T>
void linkedBinaryTree<T>::preOrder(binaryTreeNode<T>* t)
{
	if (t != NULL) {
		linkedBinaryTree<T>::visit(t);
		preOrder(t->leftChild);
		preOrder(t->rightChild);
	}
}

template<class T>
void linkedBinaryTree<T>::inOrder(binaryTreeNode<T>* t)
{
	if (t != NULL) {
		inOrder(t->leftChild);
		linkedBinaryTree<T>::visit(t);
		inOrder(t->rightChild);
	}
}

template<class T>
void linkedBinaryTree<T>::postOrder(binaryTreeNode<T>* t)
{
	if (t != NULL) {
		postOrder(t->leftChild);
		postOrder(t->rightChild);
		linkedBinaryTree<T>::visit(t);
	}

}

template<class T>
void linkedBinaryTree<T>::dispose(binaryTreeNode<T>* t)
{
	delete t;
}

template<class T>
void linkedBinaryTree<T>::output(binaryTreeNode<T>* t)
{
	cout << t->element << " ";
}




1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214

test.cpp

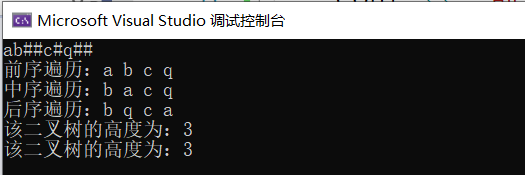
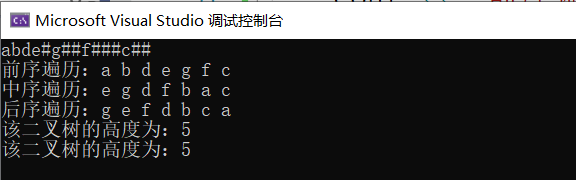
#include<iostream>
using namespace std;
#include"linkedBinaryTree.h"
#include"linkedBinaryTree.cpp"
int main() {
	linkedBinaryTree<char> binaryTree;
	binaryTree.createBinaryTree();
	cout << "前序遍历：";
	binaryTree.preOrderOutput();
	cout << "中序遍历：";
	binaryTree.inOrderOutput();
	cout << "后序遍历：";
	binaryTree.postOrderOutput();
	cout << "该二叉树的高度为：" << binaryTree.height()<<"\n";
	cout << "该二叉树的高度为：" << binaryTree.height_level()  << "\n";
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17