【数据结构】二叉搜索树_给定一个二叉搜索树(广义表形式)以及某个整数x,检查x是否在二叉搜索树上。

作者：盐析白兔 | 2024-03-12 07:37:31

踩

给定一个二叉搜索树(广义表形式)以及某个整数x,检查x是否在二叉搜索树上。

1 二叉搜索树

1.1 二叉搜索树概念

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树
若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树

1.2 二叉搜索树操作

二叉搜索树的查找
a、从根开始比较，查找，比根大则往右边走查找，比根小则往左边走查找。
b、最多查找高度次，走到到空，还没找到，这个值不存在。
二叉搜索树的插入
插入的具体过程如下：
a. 树为空，则直接新增节点，赋值给root指针
b. 树不空，按二叉搜索树性质查找插入位置，插入新节点
二叉搜索树的删除
首先查找元素是否在二叉搜索树中，如果不存在，则返回, 否则要删除的结点可能分下面四种情
况：
a. 要删除的结点无孩子结点
b. 要删除的结点只有左孩子结点
c. 要删除的结点只有右孩子结点
d. 要删除的结点有左、右孩子结点
。
实际删除时，情况a可以与情况b或者c合并起来

情况a,b,c使用托孤的方法：假设节点左子树为空，则将其双亲节点指向该节点的指针，指向该节点的右孩子。若节点右子树为空，则双亲指向左孩子。
情况d使用替换删除法：在其右子树中寻找中序下的第一个结点(关键值最小)，与被删除节点的值交换，再来处理该结点的删除问题。删除原来最小值的节点还是使用托孤的方法。

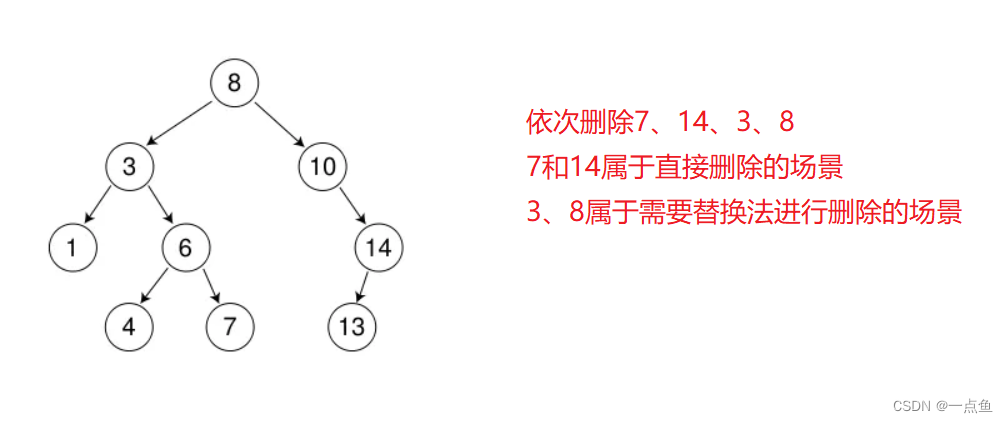
2 二叉搜索树的实现

	template<class K>
	struct BSTreeNode {
		BSTreeNode()
			:_key(-1), _left(nullptr), _right(nullptr)
		{}
		BSTreeNode(const K& key)
			:_key(key), _left(nullptr), _right(nullptr)
		{}
		BSTreeNode<K>* _left;
		BSTreeNode<K>* _right;
		K _key;
	};

	template<class K>
	class BSTree {
		typedef BSTreeNode<K> Node;

	public:
		BSTree()
			:_root(nullptr)
		{}
		BSTree(const BSTree<K>& bst) {
			_root = Copy(bst._root);
		}
		~BSTree() {
			Destroy(_root);
			_root = nullptr;
		}
		BSTree<K>& operator=(BSTree<K> bst) {// 会调用拷贝构造（可以对实参进行深拷贝），根据实参产生一颗新的树，在函数调用完会销毁
			swap(_root, bst._root); // 直接与新的树交换，还可以自动销毁原来的树；
			return *this;
		}
		bool Insert(const K& key) {
			if (_root == nullptr) {		// 首个数据插入
				_root = new Node(key);
				return true;
			}

			Node* cur = _root;
			Node* parent = nullptr;

			while (cur) {			 // 遍历查找插入位置
				if (key > cur->_key) {
					parent = cur;
					cur = cur->_right;
				}
				else if (key < cur->_key) {
					parent = cur;
					cur = cur->_left;
				}
				else {	// key 已经存在
					return false; // 插入失败
				}
			}
			// 找到了插入位置
			cur = new Node(key);
			if (key > parent->_key) {
				parent->_right = cur;
			}
			else {
				parent->_left = cur;
			}

			return true; // 插入成功
		}

		void InOrder(Node* root) { // 中序遍历
			if (root == nullptr)
				return;

			InOrder(root->_left);
			std::cout << root->_key << ' ';
			InOrder(root->_right);
		}
		void InOrder() { // 实际接口，因在类外无法直接访问_root
			InOrder(_root);
			std::cout << std::endl;
		}

		bool Find(const K& key) {
			Node* cur = _root;

			while (cur) {
				if (key > cur->_key) {
					cur = cur->_right;
				}
				else if (key < cur->_key) {
					cur = cur->_left;
				}
				else { // 找到了
					return true;
				}
			}

			return false;
		}
		
		// 托孤、替换 （找节点的左子树的最大，或者右子树的最小，替换值后，删除子节点）
		// 托孤：假设节点左子树为空，则将其双亲节点指向该节点的指针，指向该节点的右孩子。若节点右子树为空，则指向左孩子。
		bool Erase(const K& key) { 
			Node* parent = nullptr;
			Node* cur = _root;

			while (cur) {
				if (key > cur->_key) {
					parent = cur;
					cur = cur->_right;
				}
				else if (key < cur->_key) {
					parent = cur;
					cur = cur->_left;
				}
				else { // 找到了需要删除的位置
					//1、左为空 （托孤）
					if (cur->_left == nullptr) {
						if (cur == _root) {	// 需要考虑 当删除的 是头节点时
							_root = cur->_right;
						}
						else {
							if (parent->_left == cur) {
								parent->_left = cur->_right;
							}
							else {
								parent->_right = cur->_right;
							}
						}
					}
					//2、右为空（托孤）
					else if (cur->_right == nullptr) {
						if (cur == _root) { // 需要考虑 当删除的 是头节点时
							_root = cur->_left;
						}
						else {
							if (parent->_left == cur) {
								parent->_left = cur->_left;
							}
							else {
								parent->_right = cur->_left;
							}
						}
					}
					//3、左右都不为空，替换删除
					else {
						// 找右子树的最小值节点

						//Node* parent = nullptr;
						Node* parent = cur;

						Node* minRight = cur->_right;

						while (minRight->_left) {
							parent = minRight;
							minRight = minRight->_left;
						}
						cur->_key = minRight->_key;

						//parent->_left = minRight->_right;//
						
						if (minRight == parent->_left) {
							parent->_left = minRight->_right;
						}
						else {	// 如果minRight就是parent的右，则直接让parent的右指向minRight的右
							parent->_right = minRight->_right;
						}
						delete minRight;
					}
					return true; // 删除成功
				}
			}

			return false;// 删除失败，或者没找到该key
		}
	private:
		void Destroy(Node* root) { // 销毁二叉树
			if (root == nullptr) {
				return;
			}
			Destroy(root->_left);
			Destroy(root->_right);
			delete root;
		}
		Node* Copy(Node* root) { // 深拷贝
			if (root == nullptr)
				return nullptr;
			Node* newRoot = new Node(root->_key);

			newRoot->_left = Copy(root->_left);
			newRoot->_right = Copy(root->_right);

			return newRoot;
		}

		Node* _root ;
	};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194

3 二叉搜索树的应用

3.1 K模型：

K模型即只有key作为关键码，结构中只需要存储Key即可，关键码即为需要搜索到的值。

比如：给一个单词word，判断该单词是否拼写正确，具体方式如下：
以词库中所有单词集合中的每个单词作为key，构建一棵二叉搜索树
在二叉搜索树中检索该单词是否存在，存在则拼写正确，不存在则拼写错误。即上面实现的单个参数的二叉搜索树

3.2 KV模型：

每一个关键码key，都有与之对应的值Value，即<Key, Value>的键值对。该种方式在现实生活中非常常见：

比如英汉词典就是英文与中文的对应关系，通过英文可以快速找到与其对应的中文，英文单词与其对应的中文<word, chinese>就构成一种键值对；
再比如统计单词次数，统计成功后，给定单词就可快速找到其出现的次数，单词与其出现次数就是<word, count>就构成一种键值对。

简单实现：

template<class K,class V>
	class BSTree {
		typedef BSTreeNode<K,V> Node;

	public:
		BSTree()
			:_root(nullptr)
		{}
		BSTree(const BSTree<K,V>& bst) {
			_root = Copy(bst._root);
		}
		~BSTree() {
			Destroy(_root);
			_root = nullptr;
		}
		BSTree<K,V>& operator=(BSTree<K,V> bst) {// 会调用拷贝构造（可以对实参进行深拷贝），根据实参产生一颗新的树，在函数调用完会销毁
			swap(_root, bst._root); // 直接与新的树交换，还可以自动销毁原来的树；
			return *this;
		}
		bool Insert(const K& key,const V& value) {
			if (_root == nullptr) {		// 首个数据插入
				_root = new Node(key,value);
				return true;
			}

			Node* cur = _root;
			Node* parent = nullptr;

			while (cur) {			 // 遍历查找插入位置
				if (key > cur->_key) {
					parent = cur;
					cur = cur->_right;
				}
				else if (key < cur->_key) {
					parent = cur;
					cur = cur->_left;
				}
				else {	// key 已经存在
					return false; // 插入失败
				}
			}
			// 找到了插入位置
			cur = new Node(key,value);
			if (key > parent->_key) {
				parent->_right = cur;
			}
			else {
				parent->_left = cur;
			}

			return true; // 插入成功
		}

		void InOrder(Node* root) {
			if (root == nullptr)
				return;

			InOrder(root->_left);
			std::cout << root->_key << ':'<< root->_value<<std::endl;
			InOrder(root->_right);
		}
		void InOrder() {
			InOrder(_root);
		}

		Node* Find(const K& key) {
			Node* cur = _root;

			while (cur) {
				if (key > cur->_key) {
					cur = cur->_right;
				}
				else if (key < cur->_key) {
					cur = cur->_left;
				}
				else { // 找到了
					return cur;
				}
			}

			return nullptr;
		}

		bool Erase(const K& key) { // 托孤， 找左子树的最大，或者右子树的最小
			Node* parent = nullptr;
			Node* cur = _root;

			while (cur) {
				if (key > cur->_key) {
					parent = cur;
					cur = cur->_right;
				}
				else if (key < cur->_key) {
					parent = cur;
					cur = cur->_left;
				}
				else { // 找到了需要删除的位置
					//1、左为空
					if (cur->_left == nullptr) {
						if (cur == _root) {	// 需要考虑 当删除的 是头节点时
							_root = cur->_right;
						}
						else {
							if (parent->_left == cur) {
								parent->_left = cur->_right;
							}
							else {
								parent->_right = cur->_right;
							}
						}
					}
					//2、右为空
					else if (cur->_right == nullptr) {
						if (cur == _root) { // 需要考虑 当删除的 是头节点时
							_root = cur->_left;
						}
						else {
							if (parent->_left == cur) {
								parent->_left = cur->_left;
							}
							else {
								parent->_right = cur->_left;
							}
						}
					}
					//3、左右都不为空，替换删除
					else {
						// 找右子树的最小值节点

						//Node* parent = nullptr;
						Node* parent = cur;

						Node* minRight = cur->_right;

						while (minRight->_left) {
							parent = minRight;
							minRight = minRight->_left;
						}
						cur->_key = minRight->_key;
						cur->_value = minRight->_value;

						//parent->_left = minRight->_right;
						if (minRight == parent->_left) {
							parent->_left = minRight->_right;
						}
						else {	// 如果minRight就是parent的右，则直接让parent的右指向minRight的右
							parent->_right = minRight->_right;
						}
						delete minRight;
					}
					return true; // 删除成功
				}
			}

			return false;// 删除失败，或者没找到该key
		}

	private:
		void Destroy(Node* root) {
			if (root == nullptr) {
				return;
			}
			Destroy(root->_left);
			Destroy(root->_right);
			delete root;
		}
		Node* Copy(Node* root) {
			if (root == nullptr)
				return nullptr;
			Node* newRoot = new Node(root->_key,root->_value);

			newRoot->_left = Copy(root->_left);
			newRoot->_right = Copy(root->_right);

			return newRoot;
		}

		Node* _root;
	};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179

4 二叉搜索树的性能分析

二叉搜索树的插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。

对有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数，即结点越深，则比较次数越多。

但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树：
最优情况下，二叉搜索树为完全二叉树(或者接近完全二叉树)，其平均比较次数为： $log_2 N$
最差情况下，二叉搜索树退化为单支树(或者类似单支)，其平均比较次数为： $\frac{N}{2}$
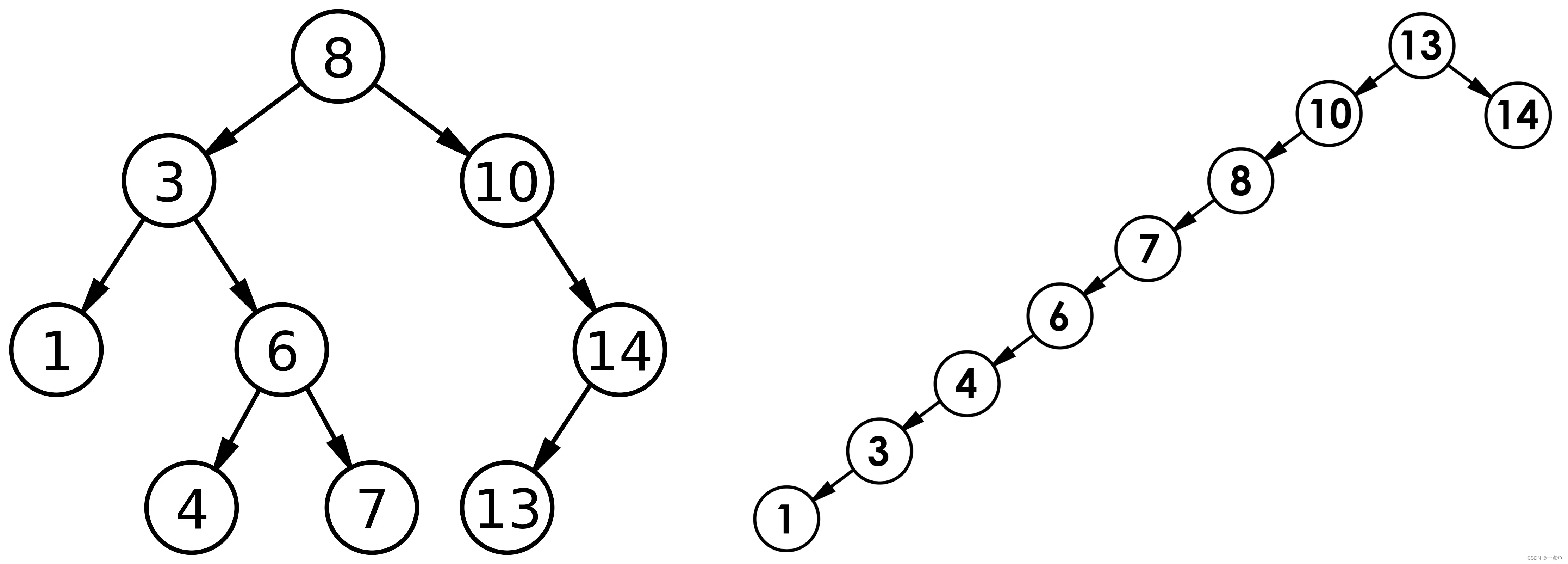
在这里插入图片描述

如果退化成单支树，二叉搜索树的性能就失去了。因此AVL平衡二叉树就出现了。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/盐析白兔/article/detail/223032