C++数据结构：二叉排序树_c++代码如何构建一个二叉排序树

二叉排序树：

• 若它的左子树不为空，则左子树上的所有节点的值均小于它的根节点的值
• 若它的右子树不为空，则右子树上的所有节点的值均大于它的根节点的值
• 它的左右子树也为二叉排序树

二叉排序树又称二叉查找树，一般使用二叉链表作为二叉排序树的存储结构。 

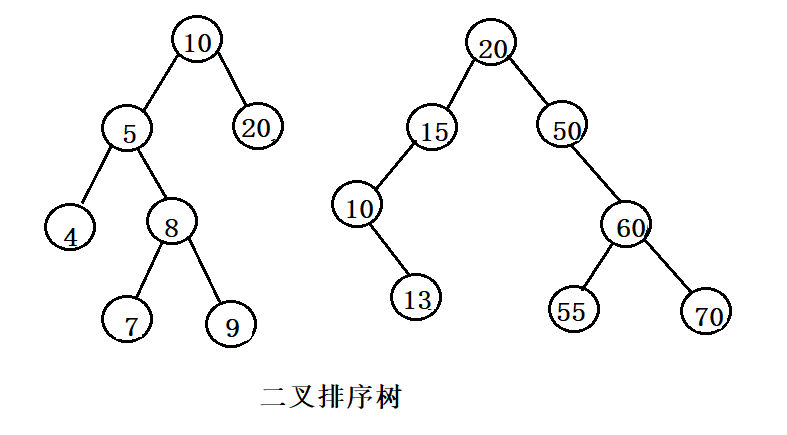
 二叉排序树结构：

 
class BST_Node
{
public:
	int data;//数据
	BST_Node* lchild;//左孩子
	BST_Node* rchild;//右孩子
	BST_Node(int i=0):data(i),lchild(nullptr),rchild(nullptr){}//构造函数
};
class BSTree
{
public:
	BST_Node* tree;
	BSTree()
	{
		tree = nullptr;//初始化
	}
 
};

二叉排序树的查找：（根据数据查找）

1. 先判断根节点是否为空和判断数据是否相同
2. 数据大于根节点，那就进入右子树
3. 数据小于根节点，那就进入左子树

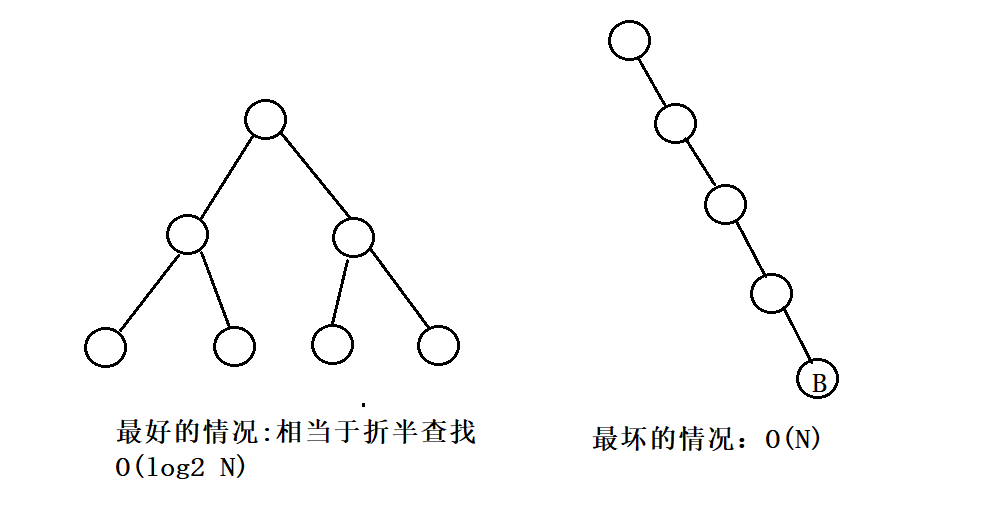
时间复杂度：

• 最好的情况：O(log2 n)
• 最坏的情况：O(n)

BST_Node* SeachBST(BST_Node* B,int K)
{
	if (!B || B->data == K)//结束条件
	{
		return B;
	}
	else if (B->data< K)
	{
		SeachBST(B->rchild, K);//进入右孩子
	}
	else
	{
		SeachBST(B->lchild, K);//进入左孩子
	}
}

 

 二叉排序树的插入：

• 若二叉排序树为空，则插入该节点，使该节点成为根节点、
• 否则，继续在左子树和右子树中寻找
  • 树中有该数据的话则不插入
  • 树中没有的话，直到找到某个叶子的左子树或右子树为空为止，则插入节点应该为该节点的左孩子或右孩子。

void insert(BST_Node*& B, int K)
{
	if (B == nullptr)//如果根节点为空，直接当成根节点
	{
		B = new BST_Node(K);
		return;//结束
	}
 
	BST_Node* B1 = B;
	BST_Node* P1=nullptr;//获取父节点位置
	while (!B1)//寻找插入位置
	{
        P1 = B1;//保存父节点
		if (K < B1->data)
		{
			B1 = B1->lchild;//如果K小于data，进入左孩子
		}
		else if(K > B1->data)
		{
			B1 = B1->rchild;//如果K大于data，进入右孩子
		}
		else
		{
			return;//相同的话，不插入，结束
		}
	}
	BST_Node* G = new BST_Node(K);//创建新节点
	if (K > P1->data)
	{
		P1->rchild = G;//作为右孩子
	}
	else
	{
		P1->lchild = G;//作为左孩子
	}
}

  二叉排序树的删除：

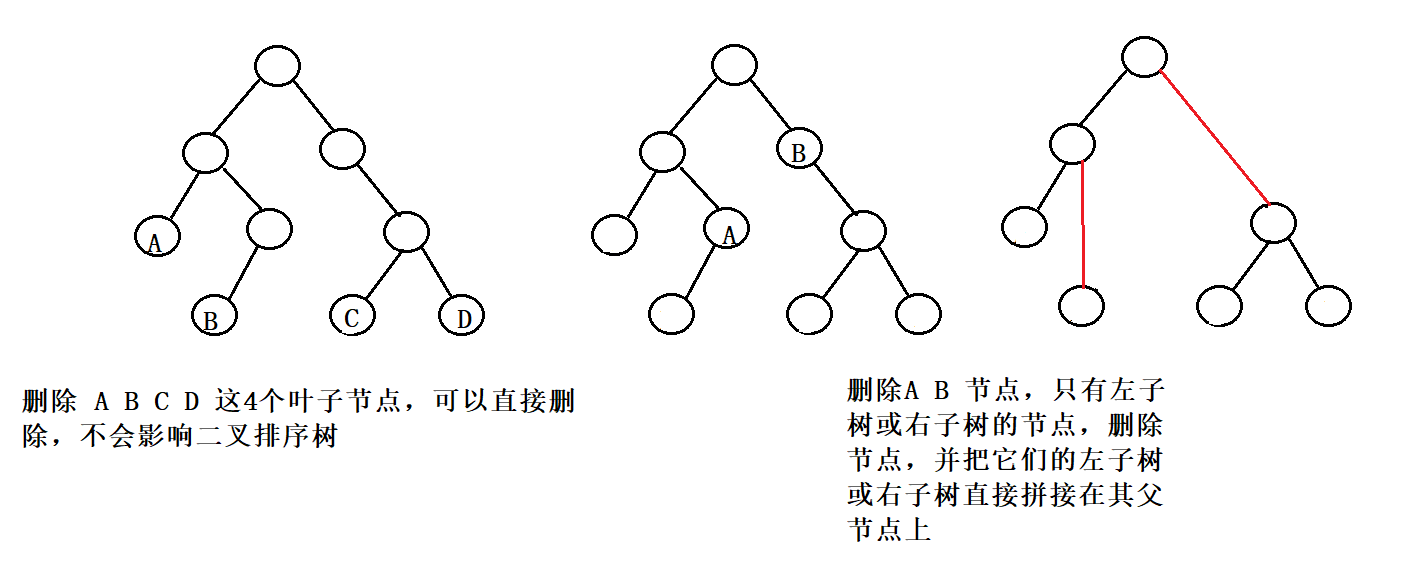
• 第一种情况：叶子节点，可以直接删除
• 第二种情况：被删除节点只有左子树或右子树，可以直接把左子树或右子树直接拼接其父节点上
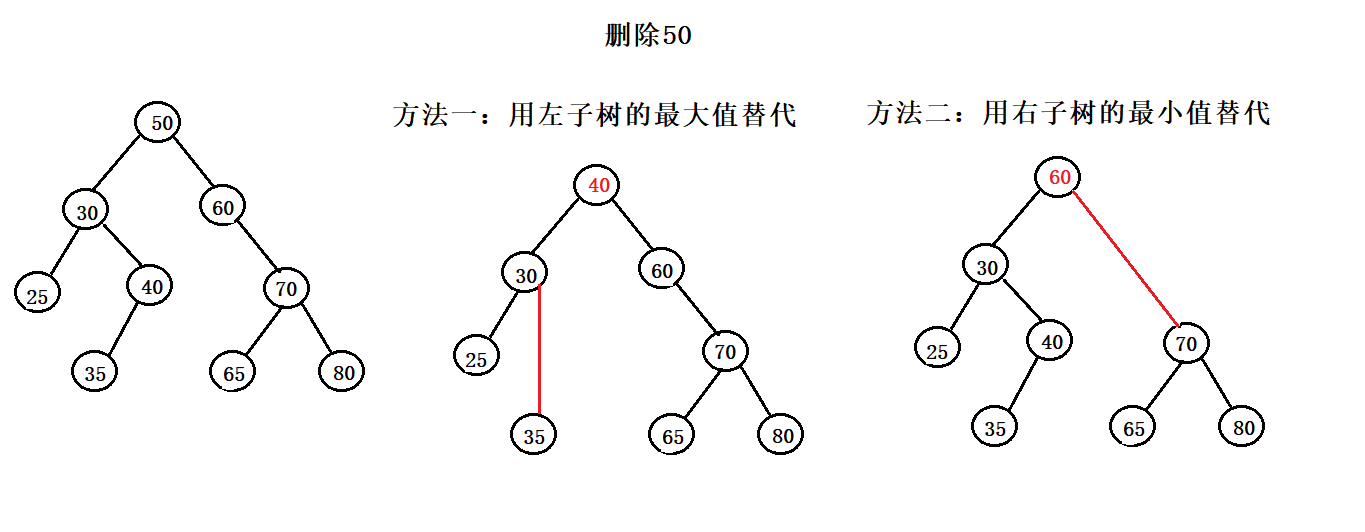
• 第三种情况：被删除节点既有左子树又有右子树
  • 可以用左子树中的最大值替换该节点，并删除该最大值节点
  • 可以用右子树中的最小值替换该节点，并删除该最小值节点

 

 

 按照以上思路写的代码，可以用查找和判段左右孩子函数来精简该代码。

void Delete(BST_Node*& B, int K)
{
	if (B == nullptr) return;//根节点为空，退出
	BST_Node* P = B;
	BST_Node* F = nullptr;//保存父节点
	while (P != nullptr)
	{
		F = P;
		if (P->data > K){
			P = P->lchild;//K小于节点数据，进入左孩子
		}
		else if (P->data < K){
			P = P->rchild;//K小于节点数据，进入右孩子
		}
		else{
			break;//找到节点退出循环
		}
	}
	if (P == nullptr)return;//如果没找到的话退出
	//查看该节点是否拥有右左子树
	if (P->lchild == nullptr && P->rchild == nullptr)//	叶子节点的话
	{
		if (F->data > P->data)F->lchild = nullptr;
		else { F->rchild = nullptr; }
		delete P;//释放节点内存
		return;
	}
	if (P->lchild != nullptr && P->rchild != nullptr)//拥有左右子树的话
	{
		//找到右子树的最小值，在该节点的右子树的左子树中
		BST_Node* M = P;//存放当前节点位置
		F = P;
		P = P->rchild;
		while (P->lchild!=nullptr)
		{
			F = P;
			P = P->lchild;//找到最小值
		}
		M->data = P->data;//数据赋值给节点
		F->lchild = nullptr;
		delete P;//释放节点内存
		return;
	}
	//单子树的情况
	if (P->lchild == nullptr && F->lchild==P)
	{
		F->lchild = P->rchild;
	}
	else if (P->lchild == nullptr && F->rchild == P)
	{
		F->rchild = P->rchild;
	}
	else if (P->rchild == nullptr && F->lchild == P)
	{
		F->lchild = P->rchild;
	}
	else
	{
		F->rchild = P->rchild;
	}
	delete P;
}