《Deep Residual Learning for Image Recognition》论文研读以及torch代码解读_deep residual learning for image recognition代码复现

Deep Residual Learning for Image Recognition

摘要：
背景：神经网络越深越难训练
解决：提出一个残差学习框架
要点：使得各个层根据输入学习残差函数F(x)而不是原始未参考的函数H(x)
结论：使得网络更容易优化，并且网络加深也不会影响准确率

1. Introduction介绍

0.plain网络

可以看到，网络越深，误差越大。

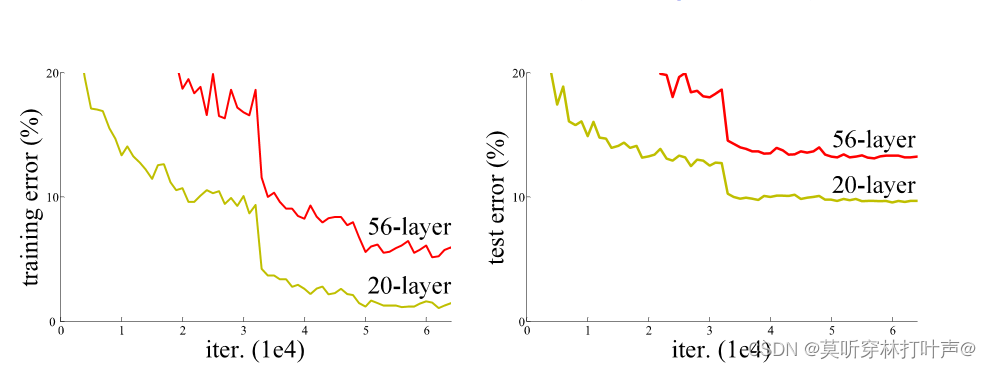
在深度学习的驱使下，一个新的问题产生了：想要训练一个更好的网络，是不是直接堆叠更多的层就行？当然不是。
网络变深了就会有梯度消失/爆炸的问题，阻止了模型的收敛。然而

1. 归一初始化normalized initialzation
2. 中间归一化intermedizte normalization

很大程度上解决了这一问题。

1.1 退化问题

当更深的网络能够开始收敛时，退化问题就暴露出来了：随着网络深度的增加，准确率会达到饱和（不足为奇），然后准确率迅速退化。但是这种退化不是由过拟合引起的，在一个合适的深度模型中增加更多的层会导致更高的训练误差。
解决方案：改变添加更多层网络的方式

• 增加的层使用恒等映射

得到两个网络，一个是较浅的普通的网络，一个是使用恒等映射的较深网络。
结果：

• 较深的模型误差更小

问题：

• 解算器无法找到与构建的解相当或者更好的解（或无法在可行的时间内找到）

直接学习H(x)比较困难，所以学习F(x)

1.2 梯度消失问题Vanishing Gradient Problem

梯度消失会阻止网络的进一步训练。
eg:sigmoid激活函数的偏导数最大值为0.25。当网络中有很多层时，导致乘积的值会减少，直到某个点损失函数的偏导数接近于0，导致偏导数消失，称之为梯度消失。
两种解决方式：

• 使用其他的激活函数ReLU()
• 构建残差块

1.3 Deep residual learning framework深度残差学习框架

构造深层网络的解决方案：

• 通过恒等映射identity mapping构建增加的层

深层模型不应该产生比浅层模型更高的训练误差。但是SGD找不到这个效果。不能直接学习H(x)。

• 本文中通过引入深度残差学习框架来解决退化问题

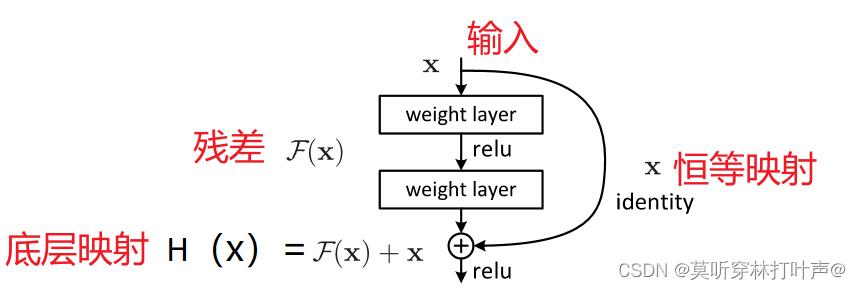
本文让网络层拟合残差映射residual mapping，而不是直接来拟合所需的底层映射desired underlying mapping。拟合F(x)，而不是拟合H(x)。
将所需的底层映射表示为H(x)，让堆叠的非线性层来拟合另一个映射F(x)=H(x)-x。原始映射被转化成F(x)+x。
我们现在是恒等映射，将x直接恒等映射过来。想要H(x)=x，即要将F(x)推至0。

Residual block把我们需要解决的问题从通过将x映射y(H(x))转变成根据x求x与y(H(x))之间的距离F(x)。所谓反向传播就是网络输出一个值，然后与真实值做比较得到的一个误差损失，同时将这个损失做差改变参数，返回的损失大小取决于原来的损失和梯度，既然目的是改变参数，而问题是改变参数的力度过小，则可以减少参数的值，使损失对参数改变的力度相对增大。

• 残差映射比原始未参考的映射unreferenced mapping更容易优化，我们要将残差推到零

F(x)+x，即为identity mapping，通过前馈神经网络的shortcut connection来实现。shortcut只执行恒等映射，不添加额外的参数和计算复杂度，整个网络仍然可以使用SGD进行计算，无需修改解算器。
152层的残差网络复杂性仍低于VGG网络。
结果：

• 残差网络更易于优化
• 相同深度的plain网络和残差网络相比，残差网络的训练误差更小
• 泛化能力更好

2.Related Work 相关工作

2.1 Residual Representations

残差向量编码比原始向量编码更加有效；
一些方法表明：良好的重构或预处理可以简化优化问题。

2.2 shortcut Connections

多层感知机、Goging、deeply都采用了shortcut Connections，解决了梯度消失/爆炸问题。
我们的公式总是学习残差函数，我们的shortcut Connections从来不关闭，所有的信息总是要通过的。

3.Deep Residual Learning 深度残差学习

3.1 Residual Learning 残差学习

假设输入维度和输出维度相同时，我们学习残差函数F(x)=H(x)-x，而不是学习H(x)，因此原始函数变成F(x)+x，但是学习的难易程度不同。

• 学习F(x)=H(x)-x=0更加容易。并且模型不会变差，因为F(x)=0时，输入输出是相等的
• 如果添加的层可以被构造为恒等映射，那么更深的模型的训练误差应该不大于与其对应的浅层网络

3.2 通过shortcuts进行恒等映射

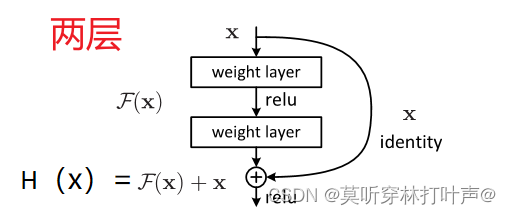
对于上面具有两层的残差块：

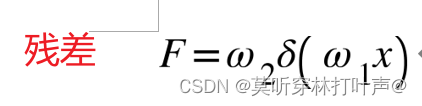
对于维度相同的映射：实线跳跃连接
残差F(x)：输入x乘第一层的权重，经过一次非线性激活，再乘第二层的权重。
再将得到的F(x)加恒等映射x后得y，再执行一次非线性激活。

对于维度不同的映射：虚线跳跃连接

这个Ws是用来匹配维度的，并且仅用来匹配维度。通过快捷连结来执行线性投影Ws来匹配维度。

一般残差块是两层或者三层的效果比较好，一层的效果没有优势。

3.3 Network Architectures网络架构

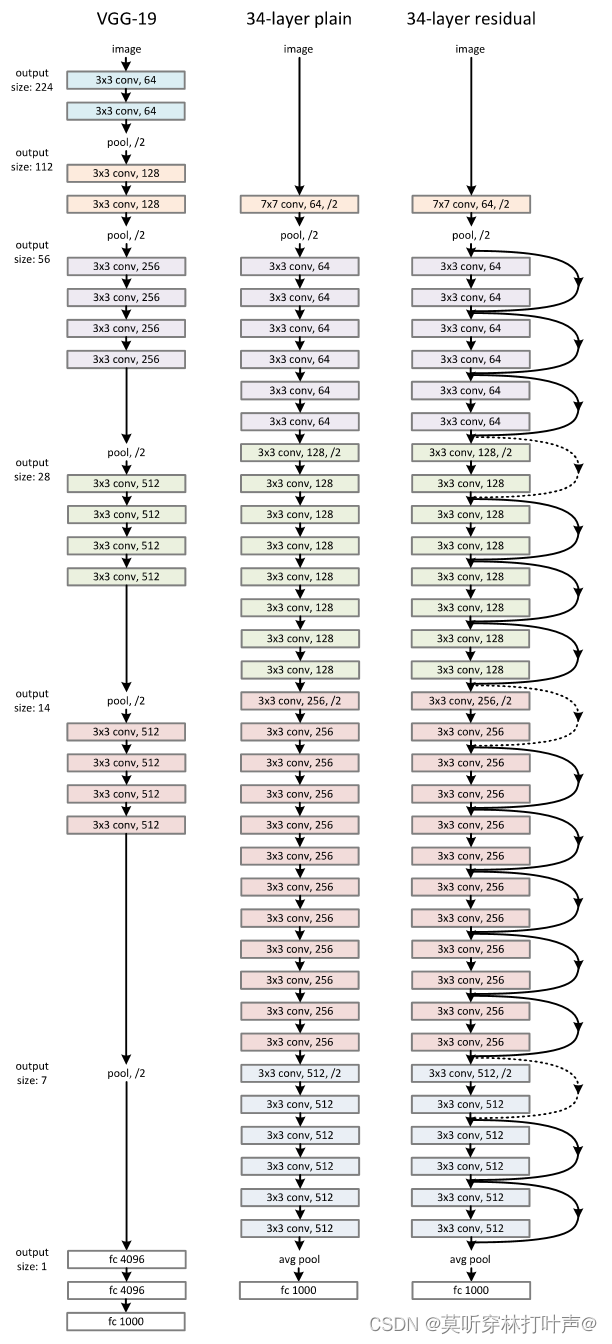
受到VGG网络的启发，采用以下原则：比VGG网有更少的卷积核和更低的复杂性
这里的验证看后续的代码

• 对于相同的特征图大小，各层具有相同数量的l滤波器
• 特征图数量减半，则滤波器数量加一倍（如果通道数/卷积核的数量翻了两倍，输入的高和宽通常都会减半）
• 步长为2的卷积层直接执行下采样（每个残差块的第一个卷积层）
• 网络以一个全局平均池化层和具有1000路全连接层的softmax结束。加权层的总数是34

当输入和输出具有相同的维度的时候：
采用shortcut实现连接方式
当输入和输出具有不同维度的时候：
一般都采用后者。

• 在增加的维度上用0来填充，不会增加额外的参数
• Ws的方式，通过1×1的卷积做映射，stride=2，在空间无作用，主要为了改变通道的维度

具体做法：

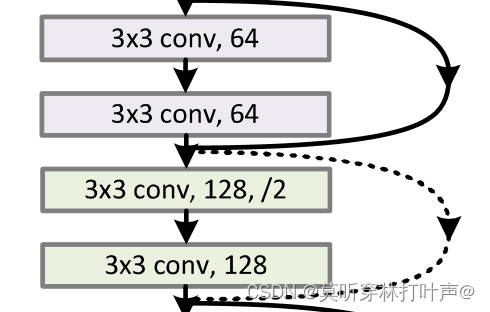
上图中的通道数从64变为128，采用的是步长为2，输出通道为128的1×1卷积来实现。

3.4 Implementation

224×224的图像，使用图像增强；
在卷积之后和激活之前都采用批量归一化（BN）；
学习率从0.1开始，误差达到稳定水平的时候/10；

4.Experiments 实验

4.1图像分类

Plain Networks： 34层比18层的误差高。但是不是由于梯度消失引起的，因为采用的BN层（BN层保证了梯度），可能是因为收敛速度太慢，影响了训练误差。
ResNet: 只是增加了恒等映射，使用0填充（无参数），34就比18好。

证明了0填充（无参数）易于训练。再证明1×1卷积的方法比0填充更好，代码几乎使用这一种方法（增加维度的使用1×1的卷积，其余为恒等映射），代码验证在后面。

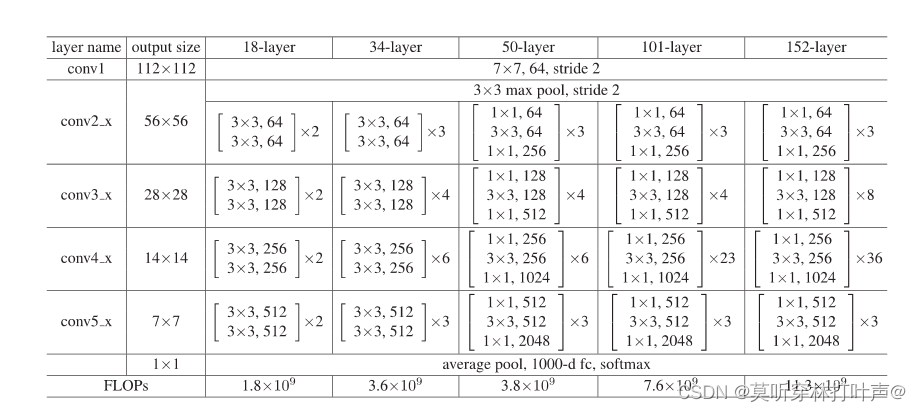
18，34采用两层的残差块，50，101，152采用三层的残差块，称为瓶颈设计bottenech design：

• 1×1 负责减少然后恢复维度
• 3×3具有较小输入/输出维度的瓶颈

4.2 在CIFAR10上的分类

不使用maxout/dropout，采用正则化来防止过拟合。残差网络只是简单的实施了正则化
展望： 结合更强的正则化来防止过拟合。

4.3 目标检测

检测方法使用区域卷积神经网络R-CNN，用残差网络代替主干网络。有提升。

5.代码

5.1 先分析pytorch提供的残差网络的源代码

参考https://blog.csdn.net/u014453898/article/details/97115891

• 观察下图，每个不同的残差网络中四个残差块的输入通道数均为：64,128,256,512，称为“基准通道数”，并且所有的输入输出通道数都是64的倍数。
• 18-layer和34-layer使用的是基础残差块(两层残差块：两个3×3的卷积层)，50-layer、101-layer、152-layer使用的瓶颈残差块(三层残差块：一层1×1的卷积层，一层3×3的卷积层，一层1×1的卷积层)。

官网：

仔细阅读源代码，找出调用顺序：
以resnet.18为例
resnet18----->_resnet---->ResNet

resnet18方法：

在自己的代码里调用时：torchvision.models.resnet18，输入相应的参数，返回_resnet

_resnet方法：

_resnet方法里的是否采用预训练：

那这些url从哪里来的？将源代码往上翻：

ResNet方法

准备工作

上文说到18-layer和34-layer使用的是基础残差块(两层残差块：两个3×3的卷积层)，50-layer、101-layer、152-layer使用的瓶颈残差块(三层残差块：一层1×1的卷积层，一层3×3的卷积层，一层1×1的卷积层)。
所以先将这两个卷积层准备好。
（1）两个卷积层

padding=1：前后左右往外扩充一格，默认填充0。
groups=1：假如输入通道数是64，输出通道数128。
stride=1：这两个卷积层的默认stride都是1。

• groups=1，输入通道数64和输出通道数128进行全卷积，即为全连接的卷积层。
• groups=2，输入通道数被分为两个32，输出通道数被分为两个64，第一个通道32和第一个通道64进行全卷积，第二个通道32和第二个通道64进行全卷积。

（2）基础残差块（两个3×3的卷积层进行堆叠）

• 第一个卷积层conv1()指定了步长为2，后面解释这里的步长为什么是2
• 第二个卷积层conv2()使用默认步长为1

由公式：得到

• 当S=2时，W会减少两倍
• 当S=1时，W是不会变的

这个原理主要用在虚线连接的地方：
①：实线连接的跳跃连接，输入通道数和输出通道数相同的情况。即上面代码downsample=none的情况。
②：conv2_x到conv3_x：虚线连接的跳跃连接（从上一个残差块到下一个残差块的跳跃连接），输入通道数和输出通道数不相同的情况，即上面代码要使用downsample进行1×1卷积转化的情况。
残差块第一层卷积层的步长为2，为了实现通道64到128的转变。
③：经过一次layer，特征图的大小减少两倍。

（3）瓶颈结构残差块（1×1、3×3、1×1）

ResNet方法

先看前向传播函数，动态是所有类型的残差函数均有4层，均调用这4层来实现。

以resnet50为例，

到ResNet里，[3,4,6,3]即为layers[0]为3，layers[1]为4，layers[2]为6，layers[3]为3。转到_make_layer函数。

_make_layer函数：

expansion就决定了选择基础残差块结构或者瓶颈结构。

使用pytorch导入神经网络

复习一下，调用函数后返回下载连接，残差块结构，残差块结构数量数的序列，是否采用预训练的模型，是否显示进度条。

import torchvision.models.resnet
resnet34=torchvision.models.resnet34(pretrained=True,progress=True)
print(resnet34)
1
2
3

结果：
可以看到，在输入四层layer之前，经历了一次步长2×2的卷积和步长2×2的最大池化层，图像已经缩小了四倍。

ResNet(
  (conv1): Conv2d(3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
  (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (relu): ReLU(inplace=True)
  (maxpool): MaxPool2d(kernel_size=3, stride=2, padding=1, dilation=1, ceil_mode=False)
  (layer1): Sequential(
    (0): BasicBlock(
      (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (1): BasicBlock(
      (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (2): BasicBlock(
      (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
  )
  (layer2): Sequential(
    (0): BasicBlock(
      (conv1): Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (downsample): Sequential(
        (0): Conv2d(64, 128, kernel_size=(1, 1), stride=(2, 2), bias=False)
        (1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (1): BasicBlock(
      (conv1): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (2): BasicBlock(
      (conv1): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (3): BasicBlock(
      (conv1): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
  )
  (layer3): Sequential(
    (0): BasicBlock(
      (conv1): Conv2d(128, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (downsample): Sequential(
        (0): Conv2d(128, 256, kernel_size=(1, 1), stride=(2, 2), bias=False)
        (1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (1): BasicBlock(
      (conv1): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (2): BasicBlock(
      (conv1): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (3): BasicBlock(
      (conv1): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (4): BasicBlock(
      (conv1): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (5): BasicBlock(
      (conv1): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
  )
  (layer4): Sequential(
    (0): BasicBlock(
      (conv1): Conv2d(256, 512, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (downsample): Sequential(
        (0): Conv2d(256, 512, kernel_size=(1, 1), stride=(2, 2), bias=False)
        (1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (1): BasicBlock(
      (conv1): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (2): BasicBlock(
      (conv1): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
  )
  (avgpool): AdaptiveAvgPool2d(output_size=(1, 1))
  (fc): Linear(in_features=512, out_features=1000, bias=True)
)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141