- 1vscode 格式化 json文件_vscode格式化json
- 2堆排序的比较次数_堆排序过程、时间复杂度分析及改进
- 3面试问题:Spring中Bean 的生命周期_springbean生命周期面试
- 4小红书 x-s x-t x-common_小红书x-s
- 5【文末送书】(蓝宝书)网络安全——CTF那些事儿_ctf 数据保护
- 6一文轻松理解和读懂Lambda表达式,附源码详细解析_lamada表达式源码解析
- 7数据智能应用系统架构:AI与大数据的融合
- 8FPGA实战进阶书籍推荐:享受编程乐趣,让编程更得心应手_fpga 书
- 92024年最新怎样将本地项目上传到gitee(使用idea或者git推送),前端面试题web
- 10在 HomeAssistant Container 版本中加入米家app_hass-xiaomi-miot
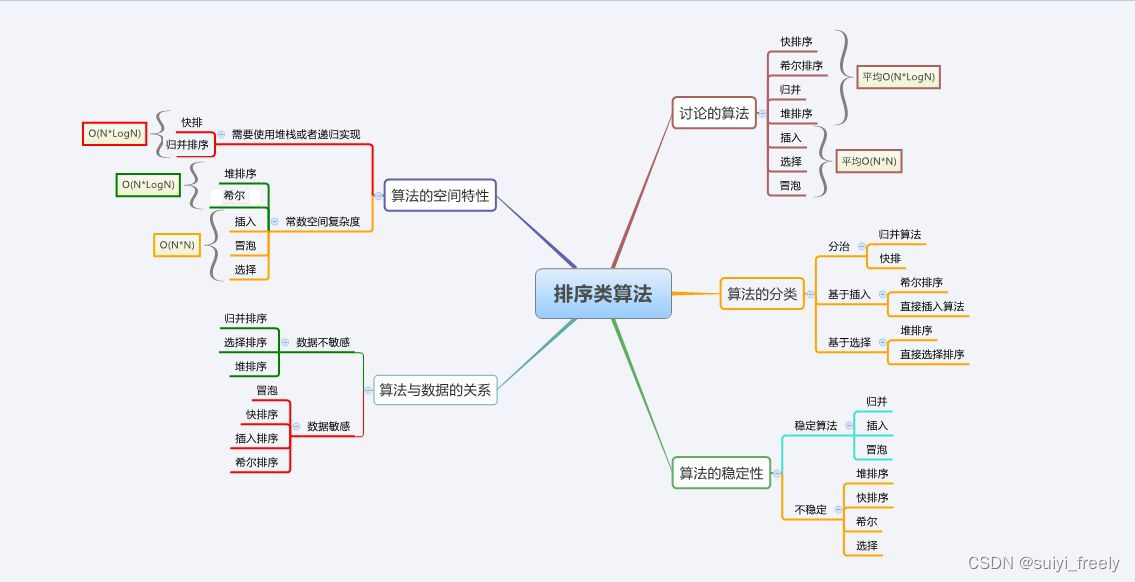
排序算法——上
赞
踩
一、冒泡排序:

1、冒泡排序算法的思想
我们从左边开始把相邻的两个数两两做比较,当一个元素大于右侧与它相邻的元素时,交换它们之间位置;反之,它们之间的位置不发生变化。冒泡排序是一种稳定的排序算法。
2、代码实现:
- void BubbleSort(int* a, int n)
- {
- for (int i = 1; i < n; i++)
- {
- for (int j = 0; j < n - i; j++)
- {
- if (a[j] > a[j + 1])
- {
- swap(&a[j], &a[j + 1]);
- }
- }
- }
- }
冒泡排序需要有两层循环,无论数组是否排好序,都会完成这两层循环,对于最差的情况,比如[9,8,7,6,5,4],对其进行升序排序,这两层循环必不可少;但是对于[9,1,2,3,4,5]这种情况,第一遍循环结束后,整个数组就已经是升序排列的了,但是普通的冒泡排序还会继续进行循环遍历比较,这就对做了不少无用功。所以需要设置一个排序完成的标志,如果排序已经完成,就没必要再继续循环遍历了,直接跳出循环。
优化版本:
- void BubbleSort(int* a, int n)
- {
- for (int i = 1; i < n; i++)
- {
- int flag = 0;
- for (int j = 0; j < n - i; j++)
- {
- if (a[j] > a[j + 1])
- {
- swap(&a[j], &a[j + 1]);
- flag = 1;
- }
- }
- if (flag == 0)
- {
- break;
- }
- }
- }

二、插入排序
1、直接插入排序:
当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移。

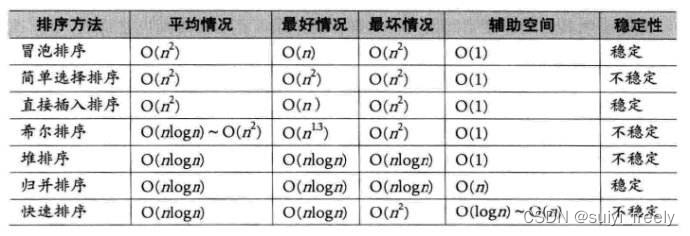
直接插入排序的特性总结:
1. 元素集合越接近有序,直接插入排序算法的时间效率越高
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1),它是一种稳定的排序算法
4. 稳定性:稳定
单趟:
- int end = i;
- int tmp = a[i + 1];
- while (end >= 0)
- {
- if (a[end] > tmp)
- {
- a[end+1] = a[end];
- end--;
- }
- else
- {
- break;
- }
- a[end+1] = tmp;
- }
这里有些同学可能会这样去写:
- int end = i;
- int tmp = a[i + 1];
- while (end >= 0)//如果写为>0则最后一个数据比较不了。
- {
- if (a[end] > tmp)
- {
- a[end+1] = a[end];
- end--;
- }
- }
- //最后出去时end为-1
- a[end+1] = tmp;
其实这样会造成不必要的比较,因为前面的数据已经排好序,所以当if条件不满足时,一定排好了序,只需将后一个数据放在end位置即可;
很多人会这么写:
- for (int i = 0; i < n ; i++)
- {
- int end = i;
- int tmp = a[i + 1];
- while (end >= 0)
- {
- if (a[end] > tmp)
- {
- a[end+1] = a[end];
- end--;
- }
- else
- {
- break;
- }
- a[end] = tmp;
- }
- }

但是实际上这样写会造成数组越界访问,[0, n-2]是最后一组[0,end]有序 end+1位置的值插入[0,end],保持有序
- void InsertSort(int* a, int n)
- {
- for (int i = 0; i < n - 1; i++)
- {
- // [0, n-2]是最后一组
- // [0,end]有序 end+1位置的值插入[0,end],保持有序
- int end = i;
- int tmp = a[i + 1];
- while (end >= 0)
- {
- if (a[end] > tmp)
- {
- a[end+1] = a[end];
- end--;
- }
- else
- {
- break;
- }
- a[end+1] = tmp;
- }
- }
- }

2、希尔排序
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达=1时,所有记录在统一组内排好序。

我们先尝试第一趟中红色组的排序:
- //对红色组
- int gap = 5;
- for (int i = 0; i < n - gap; i+=gap)
- {
- int end = i;
- int tmp = a[i + gap];
- while (end >= 0)
- {
- if (tmp < a[end])
- {
- a[end + gap] = a[end];
- end -= gap;
- }
- else
- {
- break;
- }
- a[end+gap] = tmp;
- }
- }

同理不可写为<n,因为可能造成数组越界访问。(我们不难发现其是插入排序的一种变形);
那么我们对第一趟排序就非常好写了:
1、分组排序
- int gap = 3;
- for (int j = 0; j < gap; j++)
- {
- for (size_t i = j; i < n - gap; i += gap)
- {
- int end = i;
- int tmp = a[end + gap];
- while (end >= 0)
- {
- if (tmp < a[end])
- {
- a[end + gap] = a[end];
- end -= gap;
- }
- else
- {
- break;
- }
- }
- a[end + gap] = tmp;
- }
- }

2、同时排序:
- int gap = 5;
- for (int i = j; i < n - gap; i ++)
- {
- int end = i;
- int tmp = a[end + gap];
- while (end >= 0)
- {
- if (tmp < a[end])
- {
- a[end + gap] = a[end];
- end -= gap;
- }
- else
- {
- break;
- }
- }
- a[end + gap] = tmp;
- }

虽然两个循环层数不一样但是效率是一模一样的(时间复杂度不能单看循环层数判断)。
我们知道:
gap > 1时是预排序
gap == 1时是插入排序
所以我们要想办法通过调整gap来实现插入排序:

所以每次调整为gap/3+1。
- void ShellSort(int* a, int n)
- {
- int gap = n;
- while (gap > 1)//这不可写为》=1,因为如果为1,则最后一次进去还是1,相当于多排了一次,浪费
- {
- gap = gap / 3 + 1;
- for (int i = j; i < n - gap; i++)
- {
- int end = i;
- int tmp = a[end + gap];
- while (end >= 0)
- {
- if (tmp < a[end])
- {
- a[end + gap] = a[end];
- end -= gap;
- }
- else
- {
- break;
- }
- }
- a[end + gap] = tmp;
- }
- }
-
- }

3、希尔排序时间复杂度的简单推理:
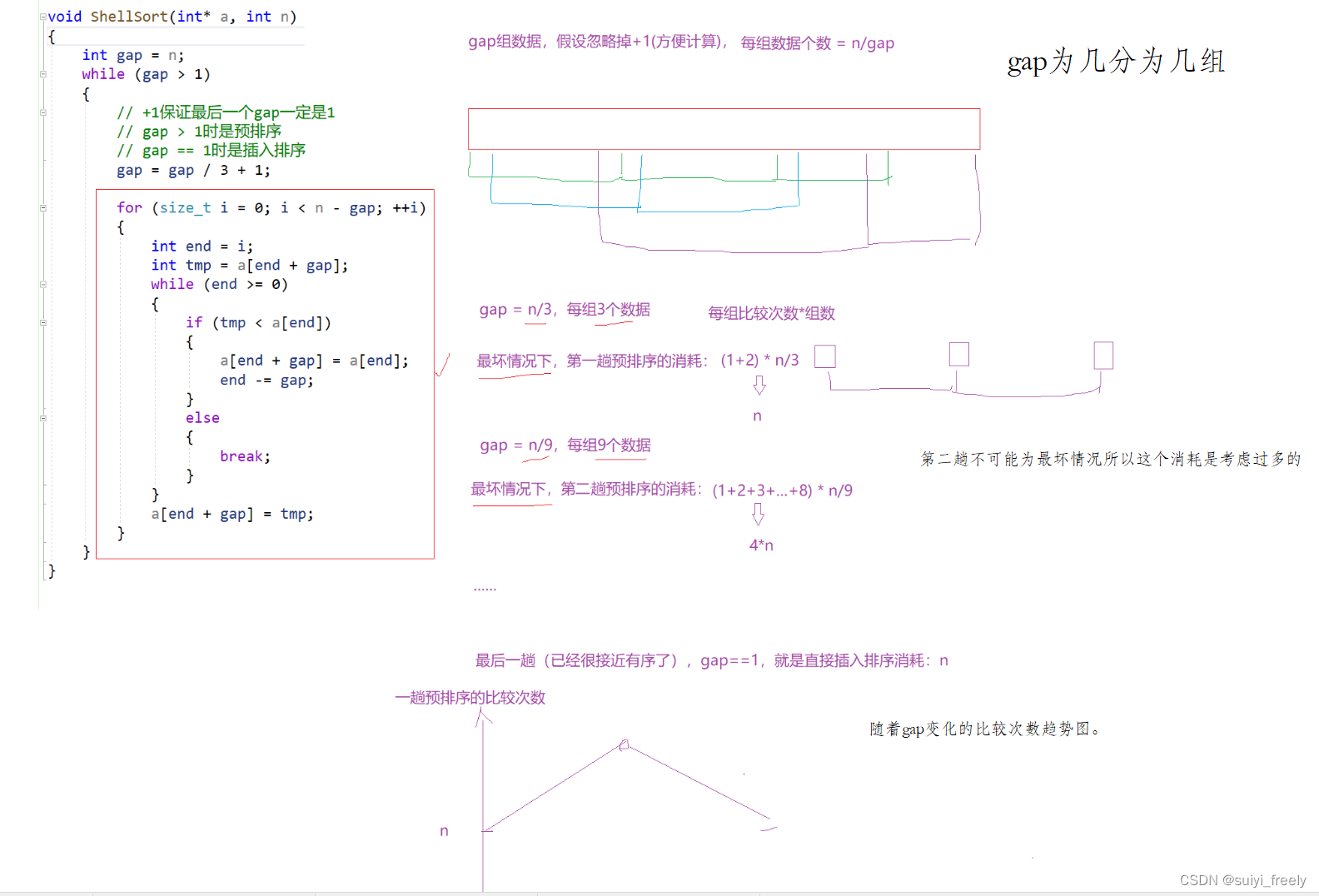
三、选择排序
选择排序( Selection sort)是一种简单直观的排序算法。它的工作原理是每一趟从待排序的数据元素中选出最小(或最大)的一个元素,顺序放在已排好序的数列的最后,直到全部待排序的数据元素排完。
选择排序算法通过选择和交换来实现排序,其排序流程如下:
(1)首先从原始数组中选择最小的1个数据,将其和位于第1个位置的数据交换。
(2)接着从剩下的n-1个数据中选择次小的1个元素,将其和第2个位置的数据交换
(3)然后,这样不断重复,直到最后两个数据完成交换。最后,便完成了对原始数组的从小到大的排序。
假如给定初始数据:(118,101,105,127,112)
一次排序:101,118,105,127,112
二次排序:101,105,118,127,112
三次排序:101,105,112,127,118
四次排序:101,105,112,118,127
(绿色为交换的数据)
每一趟在n-i+1(i=1,2,...,n-1)个记录中选取关键字最小的记录作为有序序列中第i个记录。具体来说,假设长度为n的数组arr,要按照从小到大排序,那么先从n个数字中找到最小值min1,如果最小值min1的位置不在数组的最左端(也就是min1不等于arr[0]),则将最小值min1和arr[0]交换,接着在剩下的n-1个数字中找到最小值min2,如果最小值min2不等于arr[1],则交换这两个数字,依次类推,直到数组arr有序排列。算法的时间复杂度为O(n^2)。
- void SelectSort(int* a, int n)
- {
- int begin = 0;
- int end = n - 1;
- while (begin < end)
- {
- int min = begin;
- int max = begin;
- for (int i = 0; i < n; i++)
- {
- if (a[i] < a[min])
- {
- min = i;
- }
- if (a[i] > a[max])
- {
- max = i;
- }
- swap(&a[i], &a[min]);
- swap(&a[i], &a[max]);
- begin++;
- end--;
- }
- }
- }

这么写可能会导致对于些数据无法排序;具体原因如下:
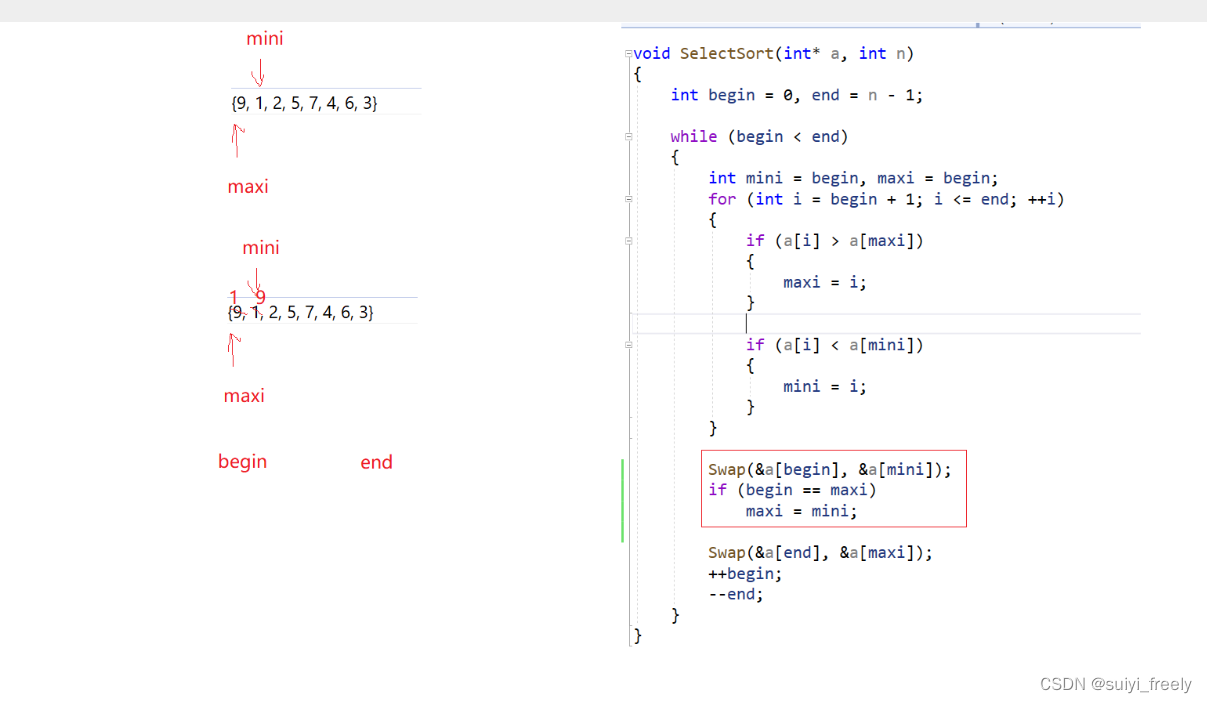
即如果先交换最小值会导致,maxi可能指向的最大值移走,使得maxi指向的并不是最大值(先换最大值也可能有类似情况发生)。
所以出现入上情况时我们要经行判断:
如果maxi等于初始位置,那么真正的最大值为mini指向的位置(因为mini会将最小值放前面);
调整代码如下:
- void SelectSort(int* a, int n)
- {
- int begin = 0;
- int end = n - 1;
- while (begin < end)
- {
- int min = begin;
- int max = begin;
- for (int i = 0; i < n; i++)
- {
- if (a[i] < a[min])
- {
- min = i;
- }
- if (a[i] > a[max])
- {
- max = i;
- }
- swap(&a[i], &a[min]);
- if (max == begin)
- {
- max = min;
- }
- swap(&a[i], &a[max]);
- begin++;
- end--;
- }
- }
- }

四、堆排序
如果不了解可以去看我写过关于堆的博客,里面有详细介绍:
http://t.csdnimg.cn/VGbOO
- void AdjustDown(int* a, int n, int parent)
- {
- // 先假设左孩子小
- int child = parent * 2 + 1;
-
- while (child < n) // child >= n说明孩子不存在,调整到叶子了
- {
- // 找出小的那个孩子
- if (child + 1 < n && a[child + 1] > a[child])
- {
- ++child;
- }
-
- if (a[child] > a[parent])
- {
- Swap(&a[child], &a[parent]);
- parent = child;
- child = parent * 2 + 1;
- }
- else
- {
- break;
- }
- }
- }
-
- void HeapSort(int* a, int n)
- {
- // 向下调整建堆 O(N)
- for (int i = (n - 1 - 1) / 2; i >= 0; i--)
- {
- AdjustDown(a, n, i);
- }
-
- // O(N*logN)
- int end = n - 1;
- while (end > 0)
- {
- Swap(&a[0], &a[end]);
- AdjustDown(a, end, 0);
- --end;
- }
- }

五、计数排序
思想:计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤:
1. 统计相同元素出现次数
2. 根据统计的结果将序列回收到原来的序列中
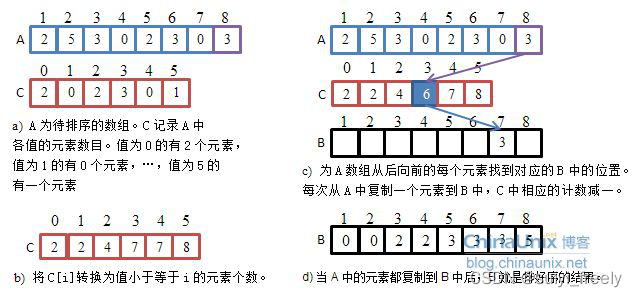
代码实现;
- void countsort(int* a, int n)
- {
- int max = a[0];
- int min = a[0];
- for (int i = 0; i < n; i++)//找到最大最小值,确定开辟空间
- {
- if (a[i] > max)
- {
- max = a[i];
- }
- if (a[i] < min)
- {
- min = a[i];
- }
- }
- int* tmp = (int*)calloc(max - min + 1, sizeof(int));
- if (tmp == NULL)
- {
- perror("calloc fail");
- return;
- }
- for (int j = 0; j < n; j++)//计数
- {
- tmp[a[j] - min]++;
- }
- // 排序
- int j = 0;
- for (int i = 0; i < max-min+1; i++)
- {
- while (tmp[i]--)
- {
- a[j++] = i + min;
- }
- }
-
- free(tmp);
- }

六、总结: