机器学习之奇异值分解 SVD_svd对角矩阵的元素

作者：Gausst松鼠会 | 2024-06-13 16:59:36

踩

svd对角矩阵的元素

奇异值分解（Singular Value decomposition SVD），更小的数据集来表示原始数据。去除噪音和冗余数据。

大致原理记录：

如果说一个向量v是方阵A的特征向量，将一定可以表示成下面的形式：
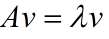在这里插入图片描述或

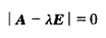
这时候λ就被称为特征向量v对应的特征值，一个矩阵的一组特征向量是一组正交向量。特征值分解是将一个矩阵分解成下面的

形式：
在这里插入图片描述
其中Q是这个矩阵A的特征向量组成的矩阵，Σ是一个对角阵，每一个对角线上的元素就是一个特征值

线性变换（矩阵近似），略。再看分解得到的Σ矩阵是一个对角阵，里面的特征值是由大到小排列的，这些特征值所对应的特征

向量就是描述这个矩阵变化方向（从主要的变化到次要的变化排列）。利用这前N个变化方向，就可以近似这个矩阵（变换）

特征值分解可以得到特征值与特征向量，特征值表示的是这个特征到底有多重要，而特征向量表示这个特征是什么，可以将

每一个特征向量理解为一个线性的子空间。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/Gausst松鼠会/article/detail/713878

机器学习之 奇异值分解 SVD_svd对角矩阵的元素