- 1【计算机网络】思科实验(11):综合实验作业之局域网与路由协议_使用3台二层交换机和1台三层交换机实现办公室内跨vlan间的通信
- 2Android 如何监控各个应用的流量和其它乱七八糟的信息_安卓系统命令行怎监测网络用量
- 3什么是数字化转型以及为什么它如此重要?_数字化转型 重要性
- 4【JavaEE】_HTML常用标签
- 5(南京观海微电子)——EDP简介_edp接口抗rf干扰
- 6Docker端口映射_docker run端口映射
- 7vue读取文件夹下面的文件名称_vue获取文件夹下文件名
- 8STM32之USART
- 9compose(docker-images)_docker compose image
- 10云计算虚拟化技术分析及其演进路线_拟态云计算升级路线图
基于PSO粒子群优化的PID控制器参数整定算法matlab仿真
赞
踩
目录
1.课题概述
基于PSO粒子群优化的PID控制器参数整定。通过PSO不断的优化,使得PID控制器的控制反馈误差逐渐接近0,在完成优化迭代之后,对应的参数,即PID控制器的参数。
2.系统仿真结果
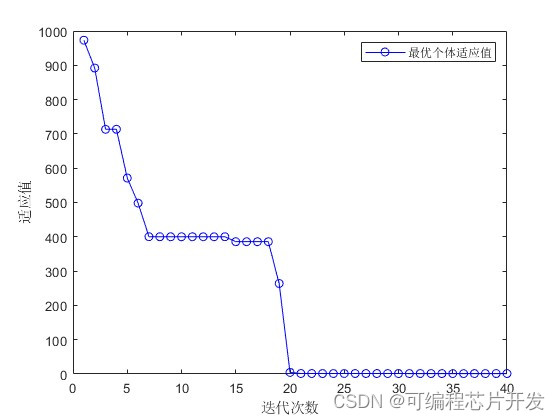

3.核心程序与模型
版本:MATLAB2022a
- ............................................................
- for jj = 1: Iteration
- jj
-
- for j=1:Npop
- %速度更新
- Vs(j,:) = 0.75*Vs(j,:) + c1*rand*(gbest(j,:) - Pops(j,:)) + c2*rand*(zbest - Pops(j,:));
- ............................................................
- %适应值
- yfits(j,:) = func_fitness(Pops(j,:));
-
- %最优更新
- if yfits(j) < fgbest(j)
- gbest(j,:) = Pops(j,:);
- fgbest(j) = yfits(j);
- end
-
- %最优更新
- if yfits(j) < fzbest
- zbest = Pops(j,:);
- fzbest = yfits(j);
- end
- end
- %保持最优值
- y_fitness(1,jj) = fzbest;
- Kps(1,jj) = zbest(1);
- Kis(1,jj) = zbest(2);
- Kds(1,jj) = zbest(3);
- end
-
- figure
- plot(y_fitness,'b-o')
- legend('最优个体适应值');
- xlabel('迭代次数');
- ylabel('适应值');
-
-
- figure
- subplot(311)
- plot(Kps,'-bs',...
- 'LineWidth',1,...
- 'MarkerSize',6,...
- 'MarkerEdgeColor','k',...
- 'MarkerFaceColor',[0.9,0.0,0.0]);
- xlabel('迭代次数');
- ylabel('参数值');
- legend('Kp');
- ylim([0,1100]);
-
- subplot(312)
- plot(Kis,'-mo',...
- 'LineWidth',1,...
- 'MarkerSize',6,...
- 'MarkerEdgeColor','k',...
- 'MarkerFaceColor',[0.5,0.9,0.0]);
- xlabel('迭代次数');
- ylabel('参数值');
- legend('Ki');
- ylim([0,30]);
-
- subplot(313)
- plot(Kds,'-r>',...
- 'LineWidth',1,...
- 'MarkerSize',6,...
- 'MarkerEdgeColor','k',...
- 'MarkerFaceColor',[0.9,0.9,0.0]);
-
- xlabel('迭代次数');
- ylabel('参数值');
- legend('Kd');
- ylim([0,500]);
- 27

4.系统原理简介
基于PSO(粒子群优化)算法的PID(比例-积分-微分)控制器参数整定是一种优化方法,用于自动调整PID控制器的参数(比例增益Kp、积分增益Ki和微分增益Kd),以达到最佳的控制性能。
4.1 PID控制器简介
PID控制器是一种广泛使用的控制算法,其输出由比例、积分和微分三个部分的线性组合构成。对于给定的系统误差e(t)(期望值与实际值之差),PID控制器的输出u(t)可以表示为:
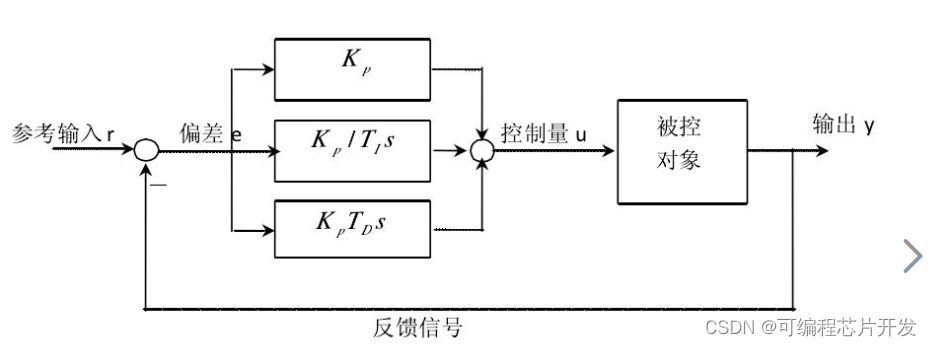
其中,( K_p )、( K_i ) 和 ( K_d ) 分别是比例、积分和微分增益。
4.2 PSO算法原理
PSO是一种基于群体智能的优化算法,通过模拟鸟群觅食行为中的社会信息共享机制来寻找问题的最优解。在PSO中,每个解被视为一个“粒子”,在搜索空间中以一定的速度和方向移动。每个粒子都有一个位置(代表解的值)和一个速度,以及一个由目标函数确定的适应度值。
粒子的速度和位置更新公式如下:
v(i)=v(i)w+c1rand*(pbest(i)-x(i))+c2*rand(gbest(i)-x(i))
x(i)=x(i)+v(i)
其中,( v_{i}(t) ) 和 ( x_{i}(t) ) 分别是粒子i在时刻t的速度和位置;( pbest_{i} ) 是粒子i的个体历史最优位置;( gbest ) 是整个群体的全局最优位置;( w ) 是惯性权重;( c_1 ) 和 ( c_2 ) 是学习因子;( r_1 ) 和 ( r_2 ) 是[0,1]之间的随机数。
4.3 基于PSO的PID参数整定
在基于PSO的PID参数整定中,我们将PID控制器的参数(( K_p ), ( K_i ), ( K_d ))编码为粒子的位置向量。目标函数通常与控制系统的性能指标相关,如误差积分(IAE)、时间乘以误差绝对值积分(ITAE)等。优化目标是最小化这个性能指标。算法步骤如下:
- 初始化粒子群,包括粒子的位置(PID参数)、速度和适应度值。
- 评估每个粒子的适应度值,即使用当前PID参数对控制系统进行仿真,并计算性能指标。
- 更新每个粒子的个体历史最优位置(pbest)和全局最优位置(gbest)。
- 根据PSO的速度和位置更新公式更新粒子的速度和位置。
- 重复步骤2-4,直到满足终止条件(如达到最大迭代次数或性能指标足够好)。
- 输出全局最优位置作为整定后的PID参数。
基于PSO的PID参数整定方法结合了PSO算法的全局搜索能力和PID控制器的简单有效性,为复杂控制系统的参数优化提供了一种有效手段。未来研究方向包括改进PSO算法以提高搜索效率、考虑控制系统的不确定性和非线性因素、以及将该方法应用于更广泛的工业控制场景。
5.完整工程文件
v


