当前位置: article > 正文

数据结构：树基础

作者：笔触狂放9 | 2024-06-24 00:56:13

踩

树基础

力扣教程

一、树

1.1、什么是树

树是一种抽象数据类型（ADT），用来模拟具有树状结构性质的数据集合，他是由n个有限节点通过连接它们的边组成的一个具有层次关系的集合

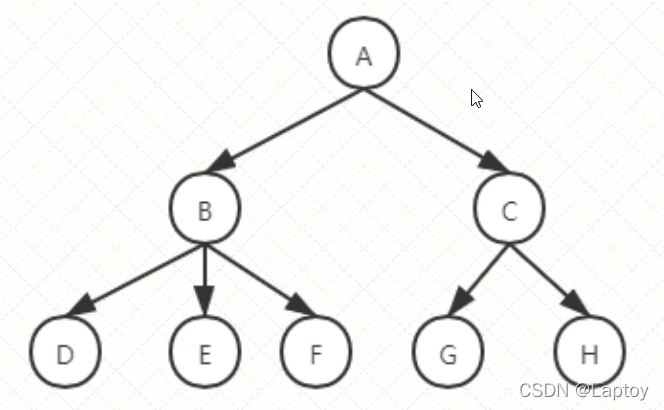
在这里插入图片描述

1.2、常用术语

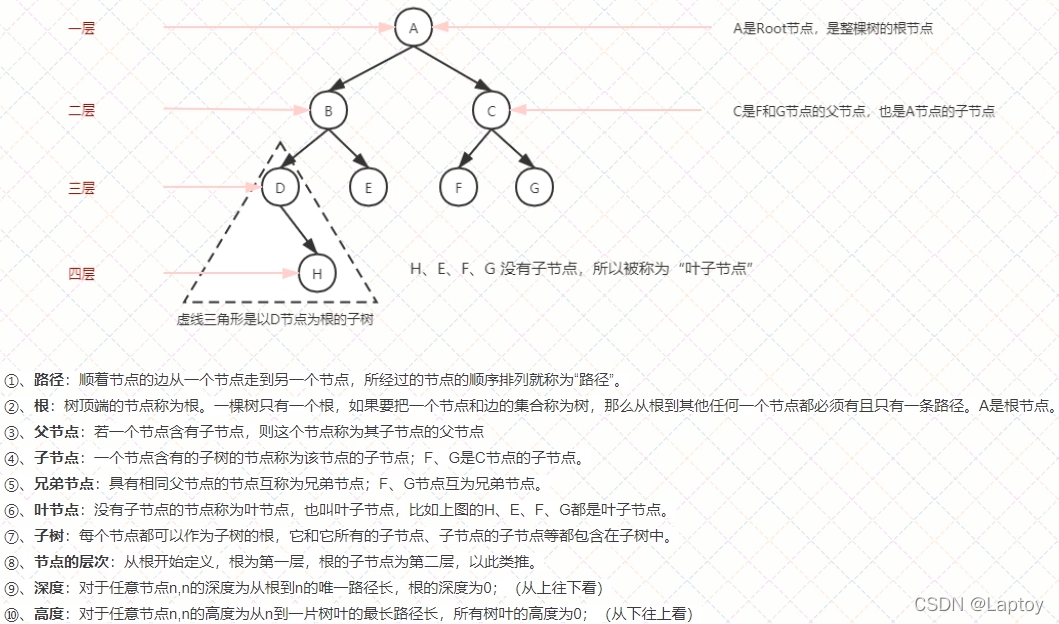
在这里插入图片描述

二、二叉树概念

2.1、基本二叉树

每个节点最多只能有两个子节点的一种形式称为二叉树

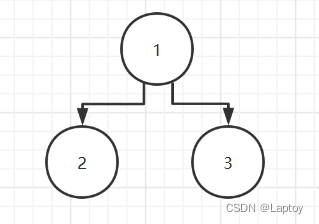
在这里插入图片描述

2.2、满二叉树

如果该二叉树的所有叶子节点都在最后一层，并且结点总数 = 2n -1，n为层数，则我们称为满二叉树。
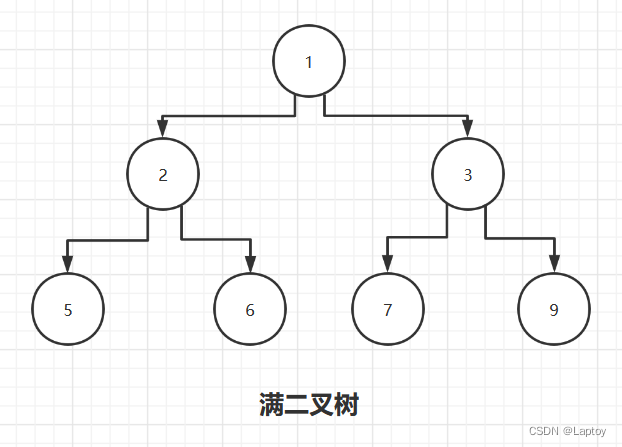
在这里插入图片描述

2.3、完全二叉树

如果该二叉树的所有叶子节点都在最后一层或者倒数第二层，而且最后一层的叶子节点在左边连续（不缺节点），倒数第二层的叶子节点在右边连续，我们称为完全二叉树

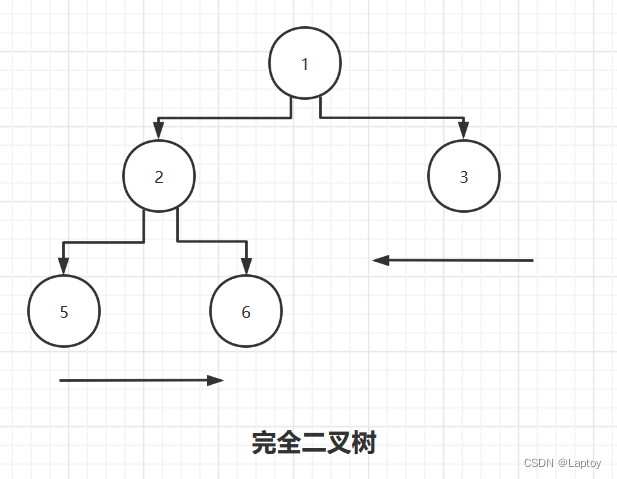
在这里插入图片描述

下图为非完全二叉树示例

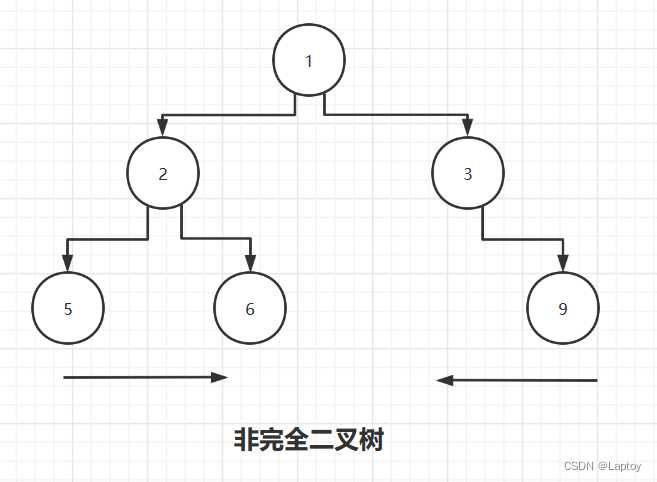
在这里插入图片描述

三、二叉树的遍历

3.1、遍历方式

可以看出按照父节点的遍历时机命名，且先左再右

前序遍历：先遍历父节点，再遍历左子节点，最后遍历右子节点
中序遍历：先遍历左子节点，再遍历父节点，最后遍历右子节点
后序遍历：先遍历左子节点，再遍历右子节点，最后遍历父节点

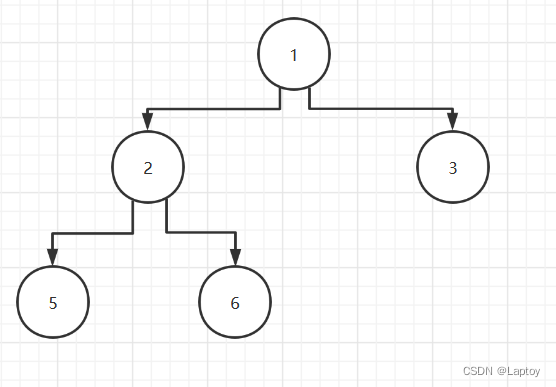
在这里插入图片描述

前序遍历结果：1、2、5、6、3
中序遍历结果：5、2、6、1、3
后序遍历结果：5、6、2、3、1

3.2、递归遍历

以该二叉树为案例进行代码演示遍历

在这里插入图片描述

1、定义节点类

class Node {
    private int id;
    private Node left;
    private Node right;

    public Node(int id) {
        this.id = id;
    }

    // 前序遍历-----》 父 左 右
    public void preOrder() {
        // 输出父节点
        System.out.println(this);
        // 递归向左子树前序遍历
        if (this.left != null) {
            this.left.preOrder();
        }
        // 递归向右子树前序遍历
        if (this.right != null) {
            this.right.preOrder();
        }
    }

    // 中序遍历-----》 左 父 右
    public void infixOrder() {
        // 递归向左子树前序遍历
        if (this.left != null) {
            this.left.infixOrder();
        }
        // 输出父节点
        System.out.println(this);
        // 递归向右子树前序遍历
        if (this.right != null) {
            this.right.infixOrder();
        }
    }

    // 后序遍历----》 左 右 父
    public void suffixOrder() {
        // 递归向左子树前序遍历
        if (this.left != null) {
            this.left.suffixOrder();
        }
        // 递归向右子树前序遍历
        if (this.right != null) {
            this.right.suffixOrder();
        }
        // 输出父节点
        System.out.println(this);
    }

	
    // Getter、Setter

    @Override
    public String toString() {
        return "Node{" + "id=" + id + '}';
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

2、定义树

// 定义树
class BinaryTree {
    private Node root;

    public void setRoot(Node root) {
        this.root = root;
    }

    // 前序遍历
    public void preOrder() {
        if (this.root != null) {
            this.root.preOrder();
        } else {
            System.out.println("二叉树为空，无法遍历");
        }
    }

    // 中序遍历
    public void infixOrder() {
        if (this.root != null) {
            this.root.infixOrder();
        } else {
            System.out.println("二叉树为空，无法遍历");
        }
    }

    // 后序遍历
    public void suffixOrder() {
        if (this.root != null) {
            this.root.suffixOrder();
        } else {
            System.out.println("二叉树为空，无法遍历");
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

3、测试前序遍历

public class Test01 {
    public static void main(String[] args) {
        BinaryTree binaryTree = new BinaryTree();
        Node a = new Node(1);
        Node b = new Node(2);
        Node c = new Node(3);
        Node e = new Node(5);
        Node f = new Node(6);

        binaryTree.setRoot(a);

        a.setLeft(b);
        a.setRight(c);
        b.setLeft(e);
        b.setRight(f);

        binaryTree.preOrder();

    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

前序遍历结果：1、2、5、6、3
中序遍历结果：5、2、6、1、3
后序遍历结果：5、6、2、3、1

3.3、迭代遍历代码演示

使用迭代对二叉树进行遍历与递归类似，不过需要自己维护一个栈用于存放节点

public class Test02 {
   public static void main(String[] args) {
      TreeNode node1 = new TreeNode(1);
      TreeNode node2 = new TreeNode(2);
      TreeNode node3 = new TreeNode(3);

      node1.left = node2;
      node1.right = node3;

      List<Integer> integers = preTraverse(node1);
      System.out.println("前序遍历结果");
      for (Integer integer : integers) {
         System.out.print(integer);
         System.out.print(" ");
      }
      System.out.println();

      List<Integer> integers2 = midTraverse(node1);
      System.out.println("中遍历结果");
      for (Integer integer : integers2) {
         System.out.print(integer);
         System.out.print(" ");
      }
      System.out.println();

      List<Integer> integers3 = lastTraverse(node1);
      System.out.println("后遍历结果");
      for (Integer integer : integers3) {
         System.out.print(integer);
         System.out.print(" ");
      }
      System.out.println();
   }

   /**
    * 使用迭代法对二叉树进行前序遍历
    * @param root 二叉树根节点
    * @return 遍历后的集合
    */
   public static List<Integer> preTraverse(TreeNode root) {
      // 用于存放结果的集合
      List<Integer> result = new ArrayList<>();

      if (root == null) {
         return result;
      }

      // 栈，用于存放遍历的节点
      Stack<TreeNode> stack = new Stack<>();
      stack.push(root);
      // 遍历二叉树
      while (!stack.isEmpty()) {
         // 栈顶元素出栈，并放入集合中
         root = stack.pop();
         result.add(root.val);
         // 先遍历右子树，将其压栈
         if (root.right != null) {
            stack.push(root.right);
         }
         // 遍历左子树,压栈
         if (root.left != null) {
            stack.push(root.left);
         }
      }
      return result;
   }

   /**
    * 使用迭代法对二叉树进行中序遍历
    * @param root 二叉树根节点
    * @return 中序遍历结果集合
    */
   public static List<Integer> midTraverse(TreeNode root) {
      List<Integer> result = new ArrayList<>();

      if (root == null) {
         return result;
      }

      Stack<TreeNode> stack = new Stack<>();

      while (root != null || !stack.isEmpty()) {
         // 节点压栈，并遍历其左子树
         while (root != null) {
            stack.push(root);
            root = root.left;
         }

         // 栈顶元素出栈，放入结果集合
         root = stack.pop();
         result.add(root.val);

         // 遍历该节点的右子树
         root = root.right;
      }
      return result;
   }

   /**
    * 使用迭代法的后序遍历
    * @param root 二叉树根节点
    * @return 后序遍历集合
    */
   public static List<Integer> lastTraverse(TreeNode root) {
      List<Integer> result = new ArrayList<>();

      if (root == null) {
         return result;
      }

      Stack<TreeNode> stack = new Stack<>();
      // 保存放入集合的右子树，避免重复放入
      TreeNode pre = null;

      while (root != null || !stack.isEmpty()) {
         while (root != null) {
            stack.push(root);
            root = root.left;
         }

         // 获取栈顶元素
         root = stack.pop();

         // 如果该元素没有右子树，或者右子树已近被遍历过了，就放入集合
         if (root.right == null || root.right == pre) {
            result.add(root.val);
            pre = root;
            root = null;
         } else {
            // 否则就继续遍历该节点的右子树
            stack.push(root);
            root = root.right;
         }
      }
      return result;
   }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137

四、二叉树的查找

在这里插入图片描述

前、中、后序查找的思路与遍历相似，当找到对应的元素时，直接返回即可

// 节点类
class Node {
    private int id;
    private Node left;
    private Node right;

    // 前序遍历查找
    public Node preOrderSearch(int id) {
        // 判断当前节点是否匹配
        if (this.id == id) {
            return this;
        }

        Node result = null;
        // 向左递归查找
        if (this.left != null) {
            result = this.left.preOrderSearch(id);
        }

        // 如果找到直接返回
        if (result != null) {
            return result;
        }

        // 向右递归查找
        if (this.right != null) {
            result = this.right.preOrderSearch(id);
        }

        return result;
    }

    // 中序遍历查找
    public Node infixOrderSearch(int id) {
        Node result = null;
        // 向左递归
        if (this.left != null) {
            result = this.left.infixOrderSearch(id);
        }

        // 如果找到直接返回
        if (result != null) {
            return result;
        }

        // 判断当前节点是否匹配
        if (this.id == id) {
            return this;
        }

        // 向右递归
        if (this.right != null) {
            result = this.right.infixOrderSearch(id);
        }

        return result;
    }

    // 后序遍历查找
    public Node suffixOrderSearch(int id) {
        Node result = null;
        // 向左递归
        if (this.left != null) {
            result = this.left.suffixOrderSearch(id);
        }

        if (result != null) {
            return result;
        }
        // 向右递归
        if (this.right != null) {
            result = this.right.suffixOrderSearch(id);
        }

        if (result != null) {
            return result;
        }

        // 判断当前节点是否匹配
        if (this.id == id) {
            return this;
        }

        return result;
    }
    
    // Getter、Getter

    @Override
    public String toString() {
        return "Node{" + "id=" + id + '}';
    }
}    
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93

// 定义树
class BinaryTree {
    private Node root;

    public void setRoot(Node root) {
        this.root = root;
    }

    // 前序遍历查找
    public Node preOrderSearch(int id) {
        if (this.root != null) {
            return this.root.preOrderSearch(id);
        } else {
            return null;
        }
    }

    // 前序遍历查找
    public Node infixOrderSearch(int id) {
        if (this.root != null) {
            return this.root.infixOrderSearch(id);
        } else {
            return null;
        }
    }

    // 前序遍历查找
    public Node suffixOrderSearch(int id) {
        if (this.root != null) {
            return this.root.suffixOrderSearch(id);
        } else {
            return null;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

public class Test01 {
    public static void main(String[] args) {
        BinaryTree binaryTree = new BinaryTree();
        Node a = new Node(1);
        Node b = new Node(2);
        Node c = new Node(3);
        Node e = new Node(5);
        Node f = new Node(6);

        binaryTree.setRoot(a);

        a.setLeft(b);
        a.setRight(c);
        b.setLeft(e);
        b.setRight(f);

        Node node = binaryTree.preOrderSearch(1);
        System.out.println(node);

    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

五、二叉树的删除

1、删除要求

如果删除的是叶子节点，则直接删除即可
如果删除的是非叶子节点，则删除该子树

2、删除思路

因为我们的二叉树是单向的，所以我们是判断当前结点的子结点是否需要删除结点，而不能去判断当前这个结点是不是需要删除结点
如果当前结点的左子结点不为空，并且左子结点就是要删除结点，就将 this.left = null，并且就返回 (结束递归删除)
如果当前结点的右子结点不为空，并且右子结点就是要删除结点，就将 this.right= null，并且就返回 (结束递归删除)
如果第2和第3步没有删除结点，那么我们就需要向左子树进行递归删除
如果4步也没有删除结点，则应当向右子树进行递归删除

// 定义树
class BinaryTree {
    private Node root;

    public void setRoot(Node root) {
        this.root = root;
    }

    // 删除
    public void deleteNode(int id) {
        if (this.root.getId() == id) {
            this.root = null;
            System.out.println("根节点被删除");
            return;
        }
        this.root.deleteNode(id);
    }
}    
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

// 节点类
class Node {
    private int id;
    private Node left;
    private Node right;

    // 删除节点
    public void deleteNode(int id) {
        //如果左子树不为空且是要查找的节点，就删除
        if (this.left != null && this.left.id == id) {
            this.left = null;
            System.out.println("删除成功");
            return;
        }

        //如果右子树不为空且是要查找的节点，就删除
        if (this.right != null && this.right.id == id) {
            this.right = null;
            System.out.println("删除成功");
            return;
        }

        if (this.left != null) {
            this.left.deleteNode(id);
        }
        if (this.right != null) {
            this.right.deleteNode(id);
        }

    }
    
    // Getter、Getter
    
    @Override
    public String toString() {
        return "Node{" + "id=" + id + '}';
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

public class Test01 {
    public static void main(String[] args) {
        BinaryTree binaryTree = new BinaryTree();
        Node a = new Node(1);
        Node b = new Node(2);
        Node c = new Node(3);
        Node e = new Node(5);
        Node f = new Node(6);

        binaryTree.setRoot(a);

        a.setLeft(b);
        a.setRight(c);
        b.setLeft(e);
        b.setRight(f);

        binaryTree.deleteNode(6);
        binaryTree.preOrder();
        
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

删除成功
Node{id=1}
Node{id=2}
Node{id=5}
Node{id=3}
1
2
3
4
5

六、顺序存储二叉树

6.1、基本说明

从数据存储来看，数组存储方式和树的存储方式可以相互转换，即数组可以转换成树，树也可以转换成数组

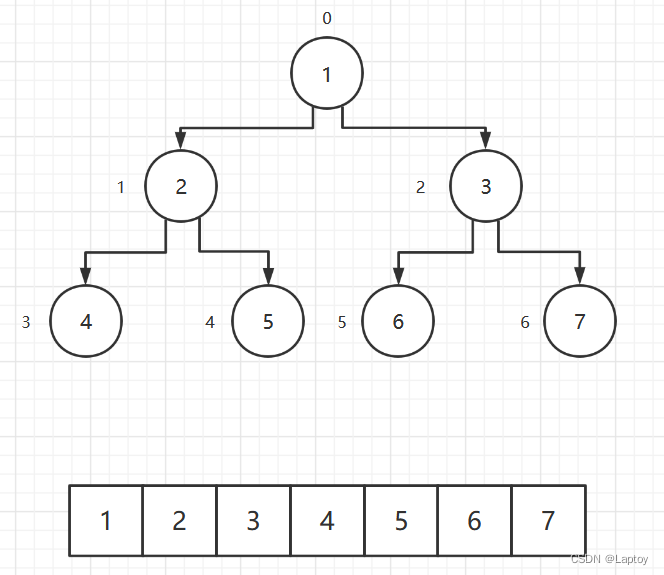
在这里插入图片描述

顺序二叉树通常只考虑完全二叉树
第n个元素的左子节点为 2 × n + 1
第n个元素的右子节点为 2 × n + 2
第n个元素的父节点为 (n - 1) ÷ 2

6.2、实现代码

public class Test02 {
    public static void main(String[] args) {
        int[] arr = {1, 2, 3, 4, 5, 6, 7};
        ArrayBinaryTree arrayBinaryTree = new ArrayBinaryTree(arr);
        arrayBinaryTree.preOrder();
    }
}

class ArrayBinaryTree {
    private int[] arr;

    public ArrayBinaryTree(int[] arr) {
        this.arr = arr;
    }

    public void preOrder(){
        this.preOrder(0);
    }

    // 二叉树前序遍历
    public void preOrder(int index) {
        if (arr == null || arr.length == 0) {
            System.out.println("数组为空");
            return;
        }
		
		// 输出当前节点
        System.out.print(arr[index] + "  ");

        // 向左
        int leftIndex = 2 * index + 1;
        if (leftIndex < arr.length) {
            preOrder(leftIndex);
        }

        // 向右
        int rightIndex = 2 * index + 2;
        if (rightIndex < arr.length) {
            preOrder(rightIndex);
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

数组前序遍历
1 2 4 5 3 6 7 
1
2

七、线索化二叉树

7.1、基本说明

因为一般的二叉树，叶子节点的左右指针都为空，这样就会造成空间的浪费。为了减少浪费，便有了线索化二叉树

n个结点的二叉链表中含有 n+1【2n-(n-1)=n+1】个空指针域
利用二叉链表中的空指针域，存放指向该结点在某种遍历次序下的前驱和后继结点的指针
这种加上了线索的二叉链表称为线索链表，相应的二叉树称为线索二叉树
根据线索性质的不同，线索二叉树可分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种
如果一个节点已经有了左右孩子，那么该节点就不能被线索化了，所以线索化二叉树后，节点的left和right有如下两种情况
- left可能指向的是左孩子，也可能指向的是前驱节点
- right可能指向的是右孩子，也可能指向的是后继节点

7.2、图解

中序线索化前

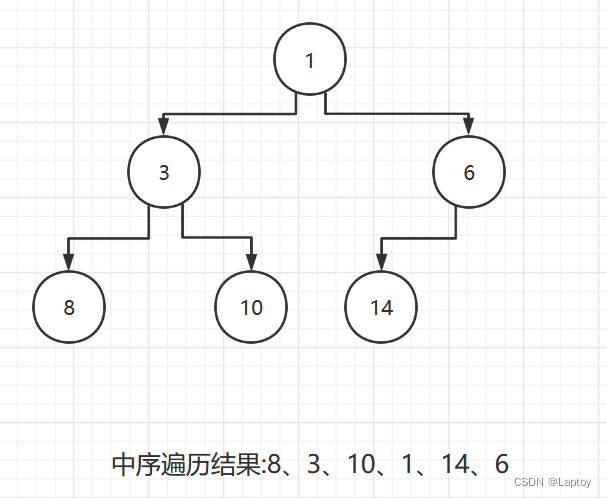
在这里插入图片描述
中序线索化后

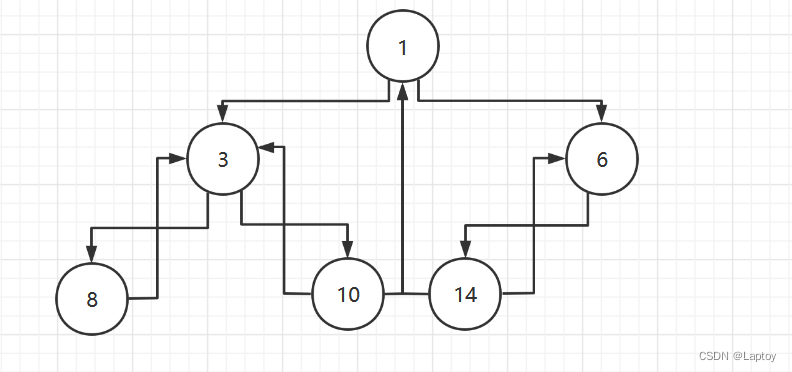
线索化思路

每个节点需要用两个变量来表示左右指针的类型（保存左右子树，还是前驱后继）
需要用两个变量来表示当前节点和当前节点的前驱节点
通过将当前节点的左指针指向前驱节点，来实现前驱节点的绑定
通过将前驱节点的右指针指向当前节点，来实现后继节点的绑定

遍历方式

各个节点可以通过线性的方式遍历，无需使用递归的方式遍历
首先有一个外循环，代替递归操作，循环条件的暂存节点不为空
第一个内循环用于找到第一个元素，然后打印
第二个循环用于找到节点的后继元素
最后将暂存节点令为右孩子

7.3、线索化实现代码

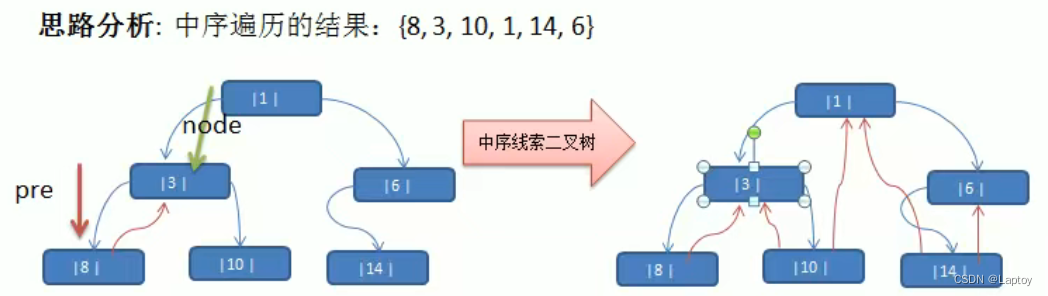
在这里插入图片描述

设当前节点为A，下一个处理的节点为B

定义临时节点 pre ，处理A后，让A变为B的前驱节点，以该临时节点在B处理时为A设置后继节点

1、定义方法

class ThreadedBinaryTree {
    private Student root;
    /**
     * 指向当前节点的前一个节点
     */
    private Student pre;

    public void setRoot(Student root) {
        this.root = root;
    }

    /**
     * 中序线索化
     *
     * @param node 当前节点
     */
    private void midThreaded(Student node) {
        if (node == null) {
            return;
        }
        // 左线索化
        midThreaded(node.getLeft());

        // 线索化当前节点
        // 如果当前节点的左指针为空，就指向前驱节点，并改变左指针类型
        if (node.getLeft() == null) {
            node.setLeft(pre);
            node.setLeftType(1);
        }
        // 通过前驱节点来将右指针的值令为后继节点
        if (pre != null && pre.getRight() == null) {
            pre.setRight(node);
            pre.setRightType(1);
        }

        // 处理一个节点后，让当前节点变为下一个节点的前驱节点
        pre = node;

        // 右线索化
        midThreaded(node.getRight());
    }

    public void midThreaded() {
        midThreaded(root);
    }

}

class Student {
    private int id;
    private String name;
    private Student left;
    private Student right;
    /**
     * 左、右指针的类型，0-->指向的是左右孩子，1-->指向的是前驱、后续节点
     */
    private int leftType = 0;
    private int rightType = 0;

    public Student(int id, String name) {
        this.id = id;
        this.name = name;
    }

	// Getter、Setter

    @Override
    public String toString() {
        return "Student{" +
                "id=" + id +
                ", name='" + name + '\'' +
                '}';
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74

2、测试

public class Test03 {
    public static void main(String[] args) {
        //初始化节点
        Student student1 = new Student(1, "A");
        Student student2 = new Student(3, "B");
        Student student3 = new Student(6, "C");
        Student student4 = new Student(8, "D");
        Student student5 = new Student(10, "E");
        Student student6 = new Student(14, "F");

        //手动创建二叉树
        ThreadedBinaryTree tree = new ThreadedBinaryTree();
        tree.setRoot(student1);
        student1.setLeft(student2);
        student1.setRight(student3);
        student2.setLeft(student4);
        student2.setRight(student5);
        student3.setLeft(student6);

        tree.midThreaded();

        //得到第五个节点的前驱节点和后继节点
        System.out.println("第五个节点的前驱节点和后继节点");
        System.out.println(student5.getLeft());  // 3
        System.out.println(student5.getRight()); // 1
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

7.4、遍历实现代码

class ThreadedBinaryTree {
    private Student root;
    /**
     * 指向当前节点的前一个节点
     */
    private Student pre;

    public void setRoot(Student root) {
        this.root = root;
    }

    /**
     * 遍历线索化后的二叉树
     */
    public void midThreadedTraverse() {
        // 暂存遍历到的节点
        Student tempNode = root;
        // 非递归的方法遍历，如果tempNode不为空就一直循环
        while (tempNode != null) {
            // 一直访问二叉树的左子树，直到某个节点的左子树指向前驱节点
            while (tempNode.getLeftType() != 1) {
                tempNode = tempNode.getLeft();
            }
            // 找到了第一个节点
            System.out.println(tempNode);
            // 再访问该节点的右子树，看是否保存了后继节点
            // 如果是，则打印该节点的后继节点信息
            while (tempNode.getRightType() == 1) {
                tempNode = tempNode.getRight();
                System.out.println(tempNode);
            }

            tempNode = tempNode.getRight();
        }

    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/笔触狂放9/article/detail/751180

数据结构：树基础

文章目录

一、树

1.1、什么是树

1.2、常用术语

二、二叉树概念

2.1、基本二叉树

2.2、满二叉树

2.3、完全二叉树

三、二叉树的遍历

3.1、遍历方式

3.2、递归遍历

3.3、迭代遍历代码演示

四、二叉树的查找

五、二叉树的删除

六、顺序存储二叉树

6.1、基本说明

6.2、实现代码

七、线索化二叉树

7.1、基本说明

7.2、图解

7.3、线索化实现代码

7.4、遍历实现代码