LinkedList 的官方文档： LinkedList (Java Platform SE 8 )
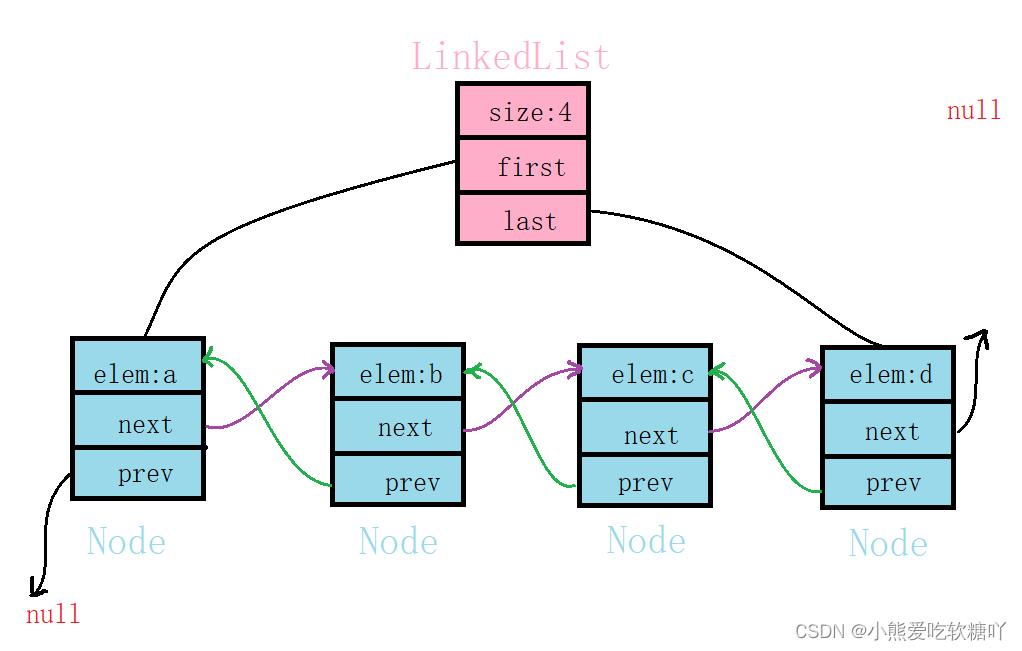
单链表从前往后遍历支持较好，从后往前遍历支持较差。因此LinkedList的底层是双向链表结构，由于链表没有将元素存储在连续的空间中，元素存储在单独的结点中，然后通过引用将结点连接起来了，因此在在任意位置插入或者删除元素时，不需要搬移元素，效率比较高。

不太清楚单链表知识的小朋友建议先看这：http://t.csdn.cn/c8WZ2

LinkedList示意图：

模拟实现LinkedList的属性：


public class MyLinkedList implements MyList {
    // 维护着 3 个属性
    // 1. 链表的头结点
    private MyNode head;
    // 2. 链表的尾结点
    private MyNode last;
    // 3. 维护着链表中的元素个数
    private int size;   // 不维护也可以通过遍历数出来，但维护好这个属性，可以让 size 的时间复杂度 O(n) -> O(1)
 
    // 构造方法
    // 构造一个空的链表
    public MyLinkedList() {
        this.head = this.last = null;
        this.size = 0;
    }

在集合框架中，LinkedList也实现了List接口，具体如下：

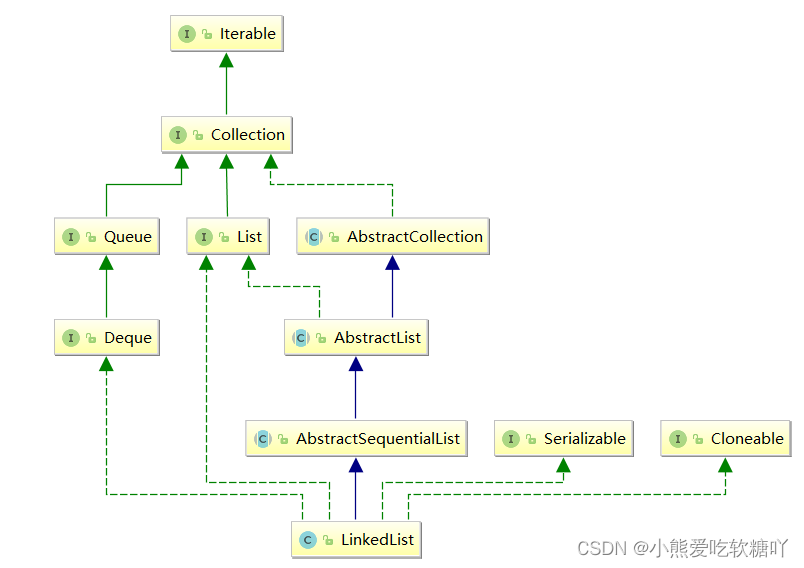
1. LinkedList实现了List接口
2. LinkedList的底层使用了双向链表
3. LinkedList没有实现RandomAccess接口，因此LinkedList不支持随机访问
比特就业课
4. LinkedList的任意位置插入和删除元素时效率比较高，时间复杂度为O(1)
5. LinkedList比较适合任意位置插入的场景

二、LinkedList的模拟实现

（1）合法LinkedList的要求

一个正确的 MyLinkedList 应该做到什么？要始终在模拟实现的过程关注以下几点内容，判断模拟的链表是否是合法的。

为了在实现LinkedList模拟过程时刻判断链表是否合法，我们可以设置一套检查装置，这套检查代码不用掌握。我们自己编写代码是要注意时刻检查调试代码是否正确，不要一股脑儿的写代码，最后bug满天飞，无法入手。

1. 得是一个合法的线性表

2. 当 head != null 则 last != null 反之亦然当 head == null 则 last == null

3. 当 head != null 的时候，则 size > 0 同理，当 head == null 的时候，则 size == 0

4. size 的值应该 == 通过遍历数出来的结点个数 (从 head 到 last 或者从 last 到 head）

5. 除了 head 和 last 之外，所有的其他结点(node), node.prev != null && node.next != null

6. head != null 时，则 head.prev == null，但 head.next 不确定（可以不为 null | size > 1）；也可以为 null | size == 1) last != null 时，则 last.next == null，但 last.prev 不确定（可以不为 null | size > 1）；也可以为 null | size == 1)

7. 除了 head 和 last 之外的所有结点(node)，node.prev.next == node && node.next.prev == node 8. 当 head.next != null 时，head.next.prev == head 当 last.prev != null 时，last.prev.next == last 9. 当 size == 1 时，head == last && head != null


private static void 断言为真(boolean condition, String message) {
        if (!condition) {
            throw new RuntimeException(message);
        }
    }
 
    private static void 检查2(MyLinkedList list) {
        if (list.head == null) {
            断言为真(list.last == null, "head 为 null 时，last 必须是 null");
        } else {
            断言为真(list.last != null, "head 不为 null 时，last 必须不为 null");
        }
    }
 
    private static void 检查3(MyLinkedList list) {
        断言为真(list.size >= 0, "size 必须 >= 0");
 
        if (list.head == null) {
            断言为真(list.size == 0, "head 为 null 时，size 必须是 0");
        } else {
            断言为真(list.size > 0, "head 不为 null 时，size 必须大于 0");
        }
    }
 
    private static int 从前往后遍历确定结点个数(MyLinkedList list) {
        int size = 0;
        for (MyNode cur = list.head; cur != null; cur = cur.next) {
            size++;
        }
 
        return size;
    }
 
    private static void 检查4(MyLinkedList list) {
        断言为真(list.size == 从前往后遍历确定结点个数(list), "记录的 size 应该和遍历出的 size 相等");
    }
 
    private static void 检查5(MyLinkedList list) {
        if (list.size > 1) {
            MyNode cur = list.head.next;
            while (cur != list.last) {
                断言为真(cur.prev != null, "非头尾结点的 prev 不能是 null");
                断言为真(cur.next != null, "非头尾结点的 next 不能是 null");
 
                cur = cur.next;
            }
        }
    }
 
    private static void 检查6(MyLinkedList list) {
        // head != null 等价于 size > 0
        if (list.head != null) {
            断言为真(list.head.prev == null, "头结点的 prev 一定是 null");
            断言为真(list.last.next == null, "尾结点的 next 一定是 null");
            if (list.size == 1) {
                断言为真(list.head.next == null, "size 为 1 时，头节点的 next 一定是 null");
                断言为真(list.last.prev == null, "size 为 1 时，为节点的 prev 一定是 null");
            } else {
                断言为真(list.head.next != null, "size > 1 时，头节点的 next 一定不是 null");
                断言为真(list.last.prev != null, "size > 1 时，尾节点的 prev 一定不是 null");
            }
 
        }
    }
 
    private static void 检查7(MyLinkedList list) {
        if (list.size > 1) {
            MyNode cur = list.head.next;    // 跳过头节点
            while (cur != list.last) {      // 跳过尾结点
                断言为真(cur.prev.next == cur, "非头尾结点的 前驱的 后继是自己");
                断言为真(cur.next.prev == cur, "非头尾结点的 后继的 前驱是自己");
 
                cur = cur.next;
            }
        }
    }
 
    private static void 检查8(MyLinkedList list) {
        // head.next != null 等价于 last.prev != null 等价于 size > 1
        if (list.size > 1) {
            断言为真(list.head.next.prev == list.head, "当 head.next != null 时，head.next.prev == head");
            断言为真(list.last.prev.next == list.last, "当 last.prev != null 时，last.prev.next == last");
        }
    }
 
    private static void 断言是一个合法的链表(MyLinkedList list) {
        检查2(list);
        检查3(list);
        检查4(list);
        检查5(list);
        检查6(list);
        检查7(list);
        检查8(list);
    }

（2）LinkedList实现的内容

//结点个数
public int size() {
return 0;
}

//链表尾插元素
public boolean add(Long e) {
return false;
}

//链表头插元素

public boolean addFirst(Long e) {

return false;

}

//指定下标插入元素
public void add(int index, Long e) {

}

//删除指定下标结点
public Long remove(int index) {
return null;
}

//删除指定元素
public boolean remove(Long e) {
return false;
}

//获取指定下标元素
public Long get(int index) {
return null;
}

//设置指定下标元素
public Long set(int index, Long e) {
return null;
}

//从前往后获取指定元素下标
public int indexOf(Long e) {
return 0;
}

//从后往前获取指定元素下标
public int lastIndexOf(Long e) {
return 0;
}

//判断是否包含指定元素
public boolean contains(Long e) {
return false;
}

//清空链表
public void clear() {

}

//判断链表是否为空
public boolean isEmpty() {
return false;
}

1.结点个数

在检查机制中已经写过一遍，就是从前往后遍历所有元素。这里主要要返回size即可


public int size() {
    return size
}

2.链表尾插元素

时间复杂度是O(1)

考虑两种情况：size==0的情况和链表size>0的情况。

注意要点：

a.需要分情况讨论。两种情况无法合并

b.既要关注head，也要关注last

c.需要正确处理结点的next和prev。涉及新加入的结点和之前的尾结点（如果存在的话）

d.size不能忘记


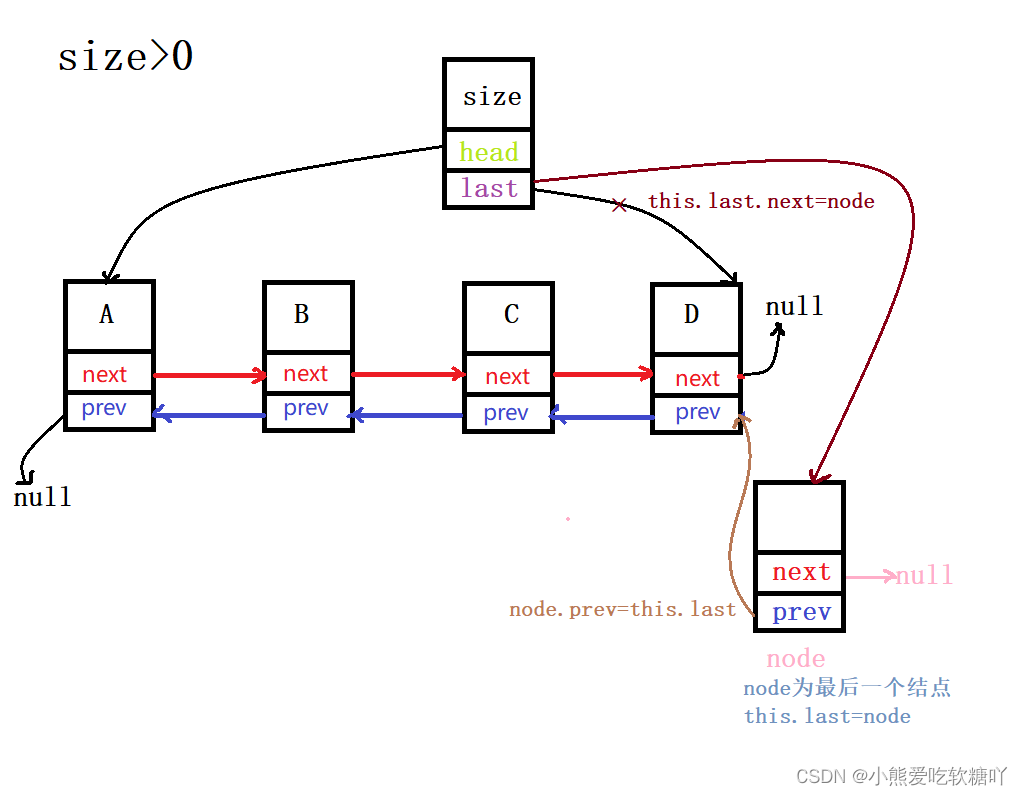
public boolean add(Long e){
    //1.将元素装入新结点
    MyNode node=new MyNode(e);
    node.next=null;//这一步可以省略
    //2.找尾结点，分情况讨论
    //2.1链表中有尾结点：last != null 等价于 head != null 等价于 size > 0
    if(size>0){
        this.last.next=node;
        node.prev=this.last;
        this.last=node;
    }else{
    //2.2链表中没有有尾结点
        node.prev=null;
        this.head=this.last=node;
    }
    //3.size个数增加
    this.size++;
    return true;
}

3.链表头插元素

时间复杂度是O(1)

与尾插思路基本一致。


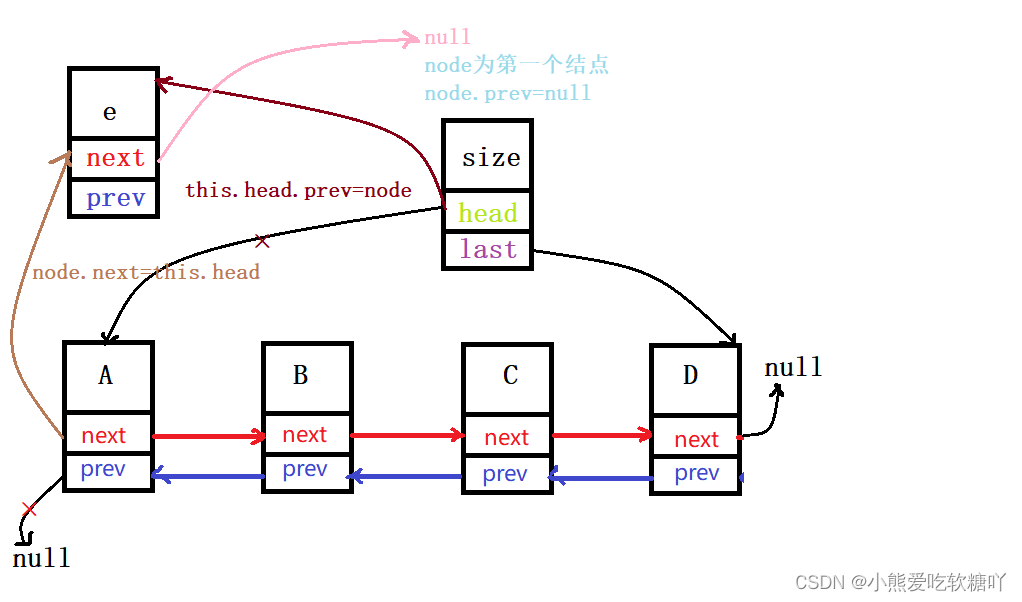
public boolean addFisrst(Long e){
    MyNode node=new MyNode(e);
    node.prev=null;
    if(size>0){
        this.head.prev=node;
        node.next=this.head;
        this.head=node;
    }else{
        node.next=null;
        this.head=this.last=node;
    }
    this.size++;
    return true;
}

4.指定下标插入元素

时间复杂度是O(n)

根据下标的特征可以分为以下几种情况。根据以下表格写代码，才可以保证所有情况都考虑到不出错。


public void add(int index,int e){
    if(index<0||index>size){
        throw new ArrayIndexOfBoundsException("下标不合法");
    }
    //情况1 size==0
    if(size==0){
        add(e);//尾插，或者addFirst(e)用头插也可以
        return;
    }
    //情况2 size==1
    if(size==1){
    //2.1 index==0
        if(index==0){
            addFirst(e);
    //2.2 index==1
        }else{
            add(e);
        }
        return;
    }
    //情况3 size>1
    //3.1 index==0
    if(index==0){
        addFirst(e);
        return;
    //3.2 index=size
    }else if(index==size){
        add(e);
        return;
    }
 
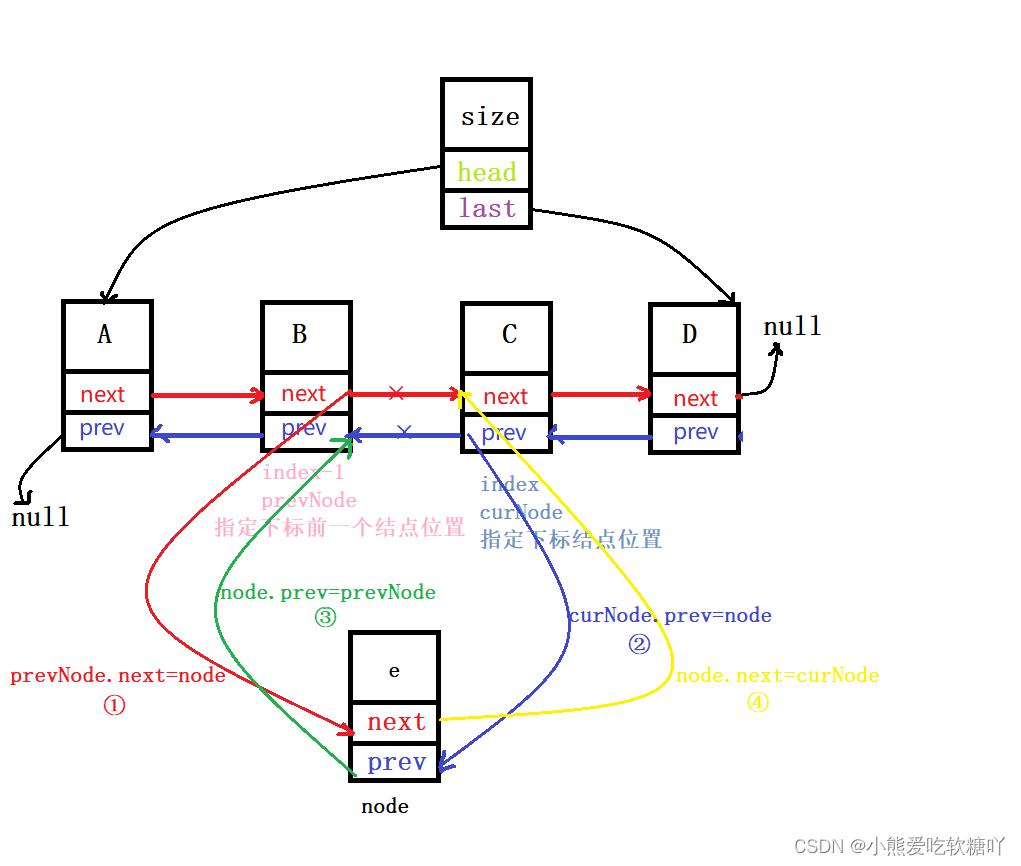
    //3.3 0<index<size
    // 链表要插入，是要找到前驱结点
    // 由于我们是双向链表，前驱结点很容易找
    // 先找到前驱结点，记为 prevNode
    
    MyNode prevNode = this.head;
    //找到指定下标的前一个位置
    for(int i=0;i<index-1;i++){
        prevNode=prevNode.next;
    }
    //找到指定下标的位置
    MyNode curNode=prevNode.next;
    //将元素e装入结点
    MyNode node=new Mynode(e);
    //将该结点插入指定下标位置处
    prevNode.next=node;
    curNode.prev=node;
    node.prev=prevNode;
    node.next=curNode;
    //size的值增加
    size++;
}

关于异常操作，指路☞ http://t.csdn.cn/QaTL8

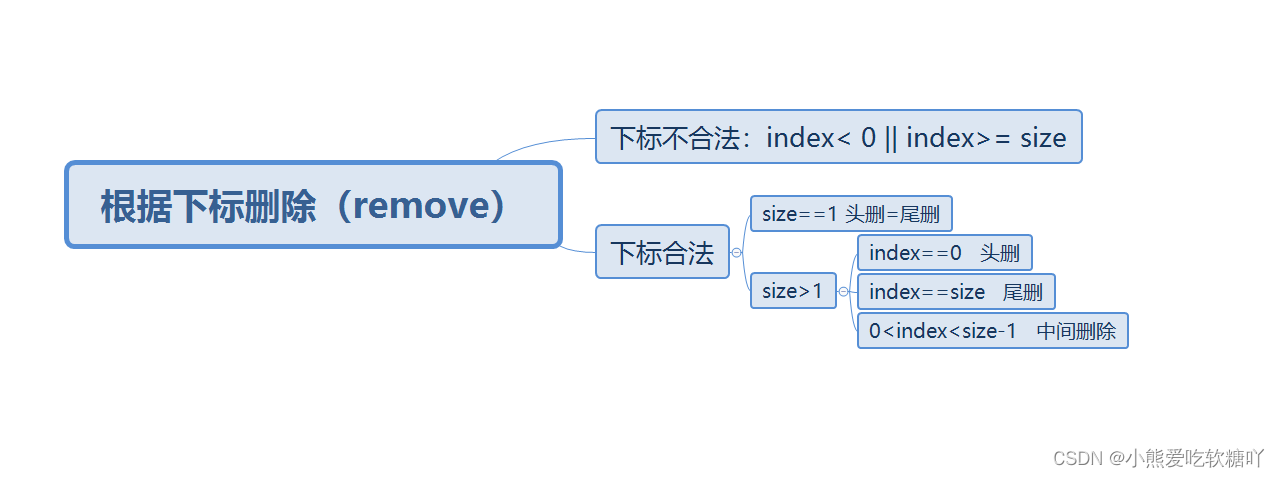
5.删除指定下标结点

时间复杂度是O(n)

注意size==0的情况是下标不合法。


public Long remove(int index){
    //下标不合法
    if(index<0||index>=size){
        throw new ArrayIndexOutOfBoundsException("下标不合法");
    }
    //下标合法
    //情况1:size==1
    if(size==1){
        //现将要删除的结点元素保存下来
        Long e=this.head.val;
        this.head=this.last=null;
        //size减少
        this.size==0;
        return e;
    }
    
    //情况2:size>1
    //2.1 index==0 头删
    if(index==0){
        Long e=this.head.val;
        //改变头结点的位置，现头结点为原来头结点的后一个
        this.head=this.head.next;
        //现头结点的前驱指向为null
        this.head.prev=null;
        //size减少
        this.size--;
        return e;
    }
    //2.2 index==size-1  尾删
    if(index==size-1){
        Long e=this.last.val;
        //改变尾结点的位置，现尾结点为原来尾结点的前一个
        this.last=this.last.prev;
        //现尾结点的前驱指向为null
        this.last.next=null;
        //size减少
        this.size--;
        return e;    
    }
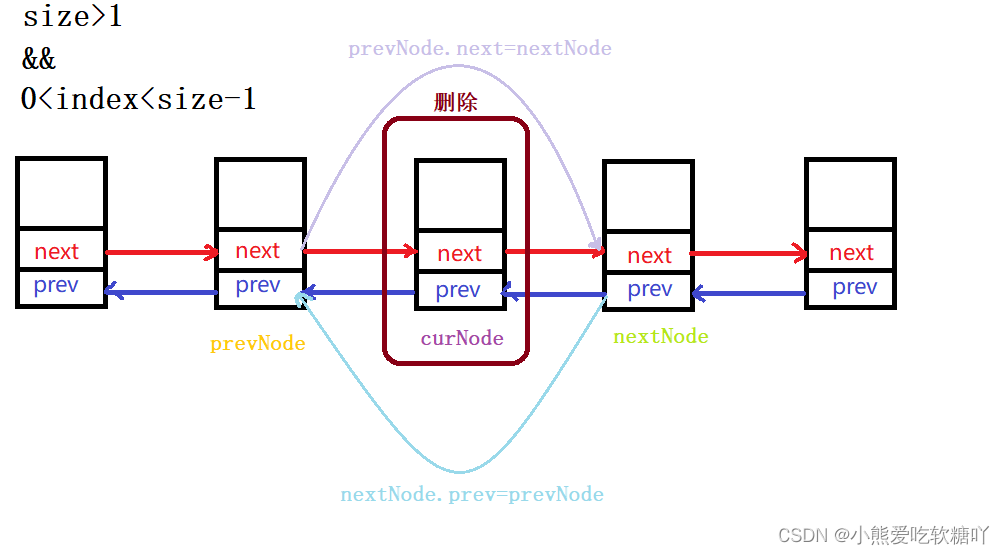
    //size>1 && 0<index<size-1
    //找到指定下标结点
    MyNode curNode=this.head;
    for(int i=0;i<index;i++){
        curNode=curNode.next;
    }
    Long e=curNode.val;
    //指定下标结点的前一个结点
    MyNode prevNode=curNode.prev;
    //指定下标结点的后一个结点
    MyNode nextNode=curNode.next;
 
    //删除操作
    preNode.next=nextNode;
    nextNode.prev=prevNode;
    this.size--;
    return e;
}

关于异常操作，指路☞ http://t.csdn.cn/QaTL8

6.删除指定元素

时间复杂度是O(n)

删除指定元素，如果找到该元素，返回true；如果没有找到该元素，返回false。


public boolean remove(Long e){
    MyNode cur=this.head;
    for(int i=0;i<size;i++){
        if(cur.val.equals(e)){
            //头删
            if(i==0){
                //size可能性>=1，分情况讨论
                this.head=this.head.next;
                // size > 1 则 此时 this.head != null
                if(this.head!=null){
                    this.head.prev==null;
                //size == 1 则 此时 this.head == null
                }else{
                    this.head=this.last=null;
                }
                this.size--;
                return true;
            }
            if(i==size-1){
                //size>1
                this.last=this.last.prev;
                this.last.next=null;
                this.size--;
                return true;
            }
            //既不是头删，也不是尾删
            MyNode prevNode =curNode.prev;
            MyNode nextNode =curNode.next;
 
            prevNode.next=nextNode;
            nextNode.next=prevNode;
            this.size--;
            return true;
        }
        cur=cur.next;//循环，写到最后别忘了
    }
    return false;        
}

7.获取指定下标元素

时间复杂度是0(n)

首先要判断下标是非合法，然后遍历获取。


public Long get(int index){    
    if(index<0||index>=size){
        throw new ArrayIndexOutOfBoundsException("下标不合法");
}
    MyNode curNode=this.head;
    for(int i=0;i<index;i++){//遍历
        curNode=curNode.next;
}
    return curNode.val;
}

8.设置指定下标元素

时间复杂度是0(n)

首先要判断下标是非合法，然后遍历获取。存储旧的结点信息。


public Long set(int index,Long e){
    if(index<0||index>=size){
        throw new ArrayIndexOutOfBoundsException("下标不合法");
    }
    MyNode curNode = this.head;
    for(int i=0;i<index;i++){//遍历
        curNode=curNode.next;
}
    Long oldValue=curNode.val;//存储旧值
    curNode.val=e;
    return oldValue;
}

9.从前往后获取指定元素下标

时间复杂度是O(n)


public int indexOf(Long e){
    int i=0;
    MyNode curNode =this.head;
    while(curNode!=null){
        if(curNode.val.equals(e)){
            return i;
        }
        i++;
        curNode=curNode.next;
    }
    return -1;
}

10.从后往前获取指定元素下标

时间复杂度是O(n)


public int lastIndexOf(Long e){
    int i=size-1;
    MyNode curNode =this.last;
    while(curNode!=null){
        if(curNode.val.equals(e)){
            return i;
        }
        i--;
        curNode=curNode.prev;
    }
    return -1;
}

11.判断是否包含指定元素

时间复杂度是O(n)


public boolean contains(Long e){
    return indexOf(e)!=-1;
}

12.清空链表

时间复杂度是O(1)


public void clear() {
    this.head = this.last = null;
    this.size = 0;
}

13.判断链表是否为空

时间复杂度是O(1)


public boolean isEmpty() {
    return size == 0;
}

三、LinkedList的使用

（1）LinkedList的构造

方法	解释
LinkedList()	无参构造
public LinkedList(Collection<? extends E> c)	使用其他集合容器中元素构造List


 public static void main(String[] args) {
    // 构造一个空的LinkedList
    List<Integer> list1 = new LinkedList<>();
    List<String> list2 = new java.util.ArrayList<>();
    list2.add("A");
    list2.add("B");
    list2.add("C");
    // 使用ArrayList构造LinkedList
    List<String> list3 = new LinkedList<>(list2);
}

（2）LinkedList的其他常用方法介绍

方法	解释
boolean add(E e)	尾插 e
void add(int index, E element)	将 e 插入到 index 位置
boolean addAll(Collection<? extends E> c)	尾插 c 中的元素
E remove(int index)	删除 index 位置元素
boolean remove(Object o)	删除遇到的第一个 o
E get(int index)	获取下标 index 位置元素
E set(int index, E element)	将下标 index 位置元素设置为 element
void clear()	清空
boolean contains(Object o)	判断 o 是否在线性表中
int indexOf(Object o)	返回第一个 o 所在下标
int lastIndexOf(Object o)	返回最后一个 o 的下标
List<E> subList(int fromIndex, int toIndex)	截取部分 list


public static void main(String[] args) {
    LinkedList<Integer> list = new LinkedList<>();
    list.add(1); // add(elem): 表示尾插
    list.add(2);
    list.add(3);
    list.add(4);
    list.add(5);
    list.add(6);
    list.add(7);
    System.out.println(list.size());
    System.out.println(list);
    // 在起始位置插入0
    list.add(0, 0); // add(index, elem): 在index位置插入元素elem
    System.out.println(list);
    list.remove(); // remove(): 删除第一个元素，内部调用的是removeFirst()
    list.removeFirst(); // removeFirst(): 删除第一个元素
    list.removeLast(); // removeLast(): 删除最后元素
    list.remove(1); // remove(index): 删除index位置的元素
    System.out.println(list);
    // contains(elem): 检测elem元素是否存在，如果存在返回true，否则返回false
    if(!list.contains(1)){
        list.add(0, 1);
    }
    list.add(1);
    System.out.println(list);
    System.out.println(list.indexOf(1)); // indexOf(elem): 从前往后找到第一个elem的位置
    System.out.println(list.lastIndexOf(1)); // lastIndexOf(elem): 从后往前找第一个1的位置
    int elem = list.get(0); // get(index): 获取指定位置元素
    list.set(0, 100); // set(index, elem): 将index位置的元素设置为elem
    System.out.println(list);
    // subList(from, to): 用list中[from, to)之间的元素构造一个新的LinkedList返回
    List<Integer> copy = list.subList(0, 3);
    System.out.println(list);
    System.out.println(copy);
    list.clear(); // 将list中元素清空
    System.out.println(list.size());
}

（3）LinkedList的遍历

a.foreach遍历

b.迭代器正向遍历

c.迭代器负向遍历


public static void main(String[] args) {
    LinkedList<Integer> list = new LinkedList<>();
    list.add(1); // add(elem): 表示尾插
    list.add(2);
    list.add(3);
    list.add(4);
    list.add(5);
    list.add(6);
    list.add(7);
    System.out.println(list.size());
    // foreach遍历
    for (int e:list) {
        System.out.print(e + " ");
    } 
    System.out.println();
    // 使用迭代器遍历---正向遍历
    ListIterator<Integer> it = list.listIterator();
    while(it.hasNext()){
        System.out.print(it.next()+ " ");
    } 
    System.out.println();
    // 使用反向迭代器---反向遍历
    ListIterator<Integer> rit = list.listIterator(list.size());
    while (rit.hasPrevious()){
        System.out.print(rit.previous() +" ");
    } 
    System.out.println();
}

四、ArrayList与LinkedList的比较

不同点	ArrayList	LinkedList
存储空间上	物理上一定连续	逻辑上连续，但物理上不一定连续
随机访问	支持O(1)	不支持：O(N)
头插	需要搬移元素，效率低O(N)	只需修改引用的指向，时间复杂度为O(1)
插入	空间不够时需要扩容	没有容量的概念
应用场景	元素高效存储+频繁访问	任意位置插入和删除频繁

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/笔触狂放9/article/detail/736606