transformer的原理_transformer原理

整体结构

transformer是一个encoeder decoder结构， 像是seq2seq一样， 但seq2seq 最大的问题在于将 Encoder 端的所有信息压缩到一个固定长度的向量中，并将其作为 Decoder 端首个隐藏状态的输入，来预测 Decoder 端第一个单词 (token) 的隐藏状态。在输入序列比较长的时候，这样做显然会损失 Encoder 端的很多信息，而且这样一股脑的把该固定向量送入 Decoder 端，Decoder 端不能够关注到其想要关注的信息。Transformer 不但对 seq2seq 模型这两点缺点有了实质性的改进 (多头交互式 attention 模块)，而且还引入了 self-attention 模块，让源序列和目标序列首先 “自关联” 起来，这样的话，源序列和目标序列自身的 embedding 表示所蕴含的信息更加丰富，而且后续的 FFN 层也增强了模型的表达能力，并且 Transformer 并行计算的能力远远超过了 seq2seq 系列模型。
我们接下来逐一解释。

Transformer Encoder

1. Positional Encoding $ Input Embedding

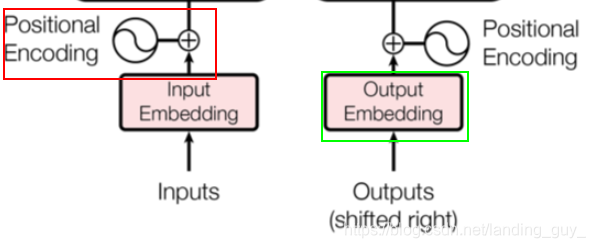
Transformer 是以字作为输入，将字进行字嵌入之后，再与位置嵌入进行相加（不是拼接，就是单纯的对应位置上的数值进行加和）
由于 Transformer 模型没有循环神经网络的迭代操作，所以我们必须提供每个字的位置信息给 Transformer，这样它才能识别出语言中的顺序关系。 就比如一句话，I love you, 这里每个字都是有位置信息的，是字而不是字母。就是图中红框部分，为每个字添加位置信息。
Embedding是因为一开始seq序列中的每个字并没有一个向量来表示它， 一开始的输入维度假如是[batch_size sequence_length], 经过embedding后变为[batch_size sequence_length embedding_dim], 如图中绿框部分.
因为是位置信息与embedding信息进行加和, 所以其维度是一致的, 都是[batch_size sequence_length embedding_dim]

如果让我们从 0 开始设计一个 Positional Encoding，比较容易想到的第一个方法是取 [0,1] 之间的数分配给每个字，其中 0 给第一个字，1 给最后一个字，具体公式就是 $PE\text{=}\frac{pos}{T-1}$, $pos\in [0,T\text{-}1]$。
这样做的问题在于，假设在较短文本中任意两个字位置编码的差为 0.0333，同时在某一个较长文本中也有两个字的位置编码的差是 0.0333。假设较短文本总共 30 个字，那么较短文本中的这两个字其实是相邻的；假设较长文本总共 90 个字，那么较长文本中这两个字中间实际上隔了两个字。这显然是不合适的，因为相同的差值，在不同的句子中却不是同一个含义

另一个想法是线性的给每个时间步分配一个数字，也就是说，第一个单词被赋予 1，第二个单词被赋予 2，依此类推。这种方式也有很大的问题：1. 它比一般的字嵌入的数值要大，难免会抢了字嵌入的「风头」，对模型可能有一定的干扰；2. 最后一个字比第一个字大太多，和字嵌入合并后难免会出现特征在数值上的倾斜

理想情况下，位置嵌入的设计应该满足以下条件：

• 它应该为每个字输出唯一的编码
• 不同长度的句子之间，任何两个字之间的差值应该保持一致
• 它的值应该是有界的

Transformer中的位置嵌入不是一个数字, ，而是一个包含句子中特定位置信息的 $d$ 维向量, 因为要和embedding后相加, 所以$d$ 其实就是embedding的维度. 这部分的公式如下:
pos表示单词在句子中的绝对位置，pos=0，1，2…，例如：Jerry在"Tom chase Jerry"中的pos=2；dmodel表示词向量的维度，在这里dmodel=512；2i和2i+1表示奇偶性，i表示词向量中的第几维，例如这里dmodel=512，故i=0，1，2…255。 注意i的取值范围, 小于一半, 很容易理解.

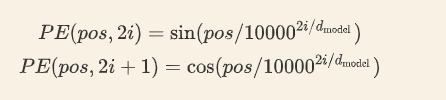
这样每个索引就会分配一个d维的位置向量, 这里图有些错误, 应该是2i和2i+1为0和1, i是0

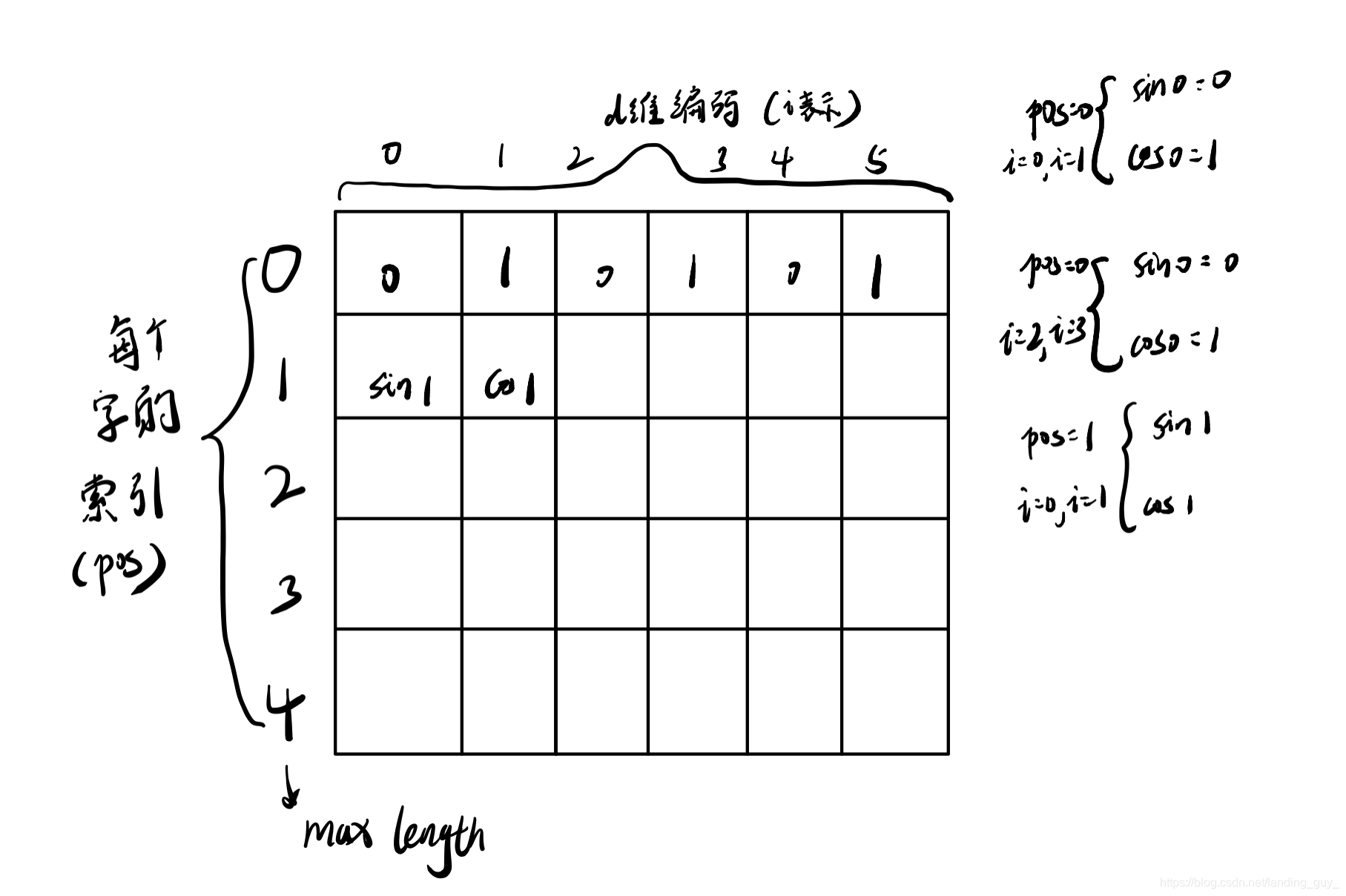
最终结果如图:
行就是字的索引, 行是编码的维度, 结果就是两维的矩阵

2. Self Attention Mechanism

对于输入的x, 经过embedding和Positional Encoding相加后分别乘三个矩阵$W_Q$, $W_K$, $W_V$, 然后会得到三个新向量, 对所有的字来说这三个矩阵都是一样的

1. 第一步是求出第一个字和所有字的相关程度, 具体来说就是第一个字的$q$向量乘所有字的$k$向量.
   
   同理第二个字的$q$和其余所有的$k$相乘
   
   最后我们就可以得到一个注意力矩阵
   

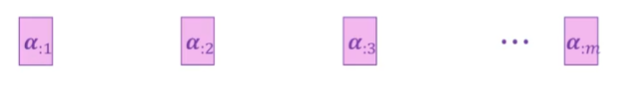
也就是得到类似下面的图, 行是字的索引, 列是代表和m个字进行注意力计算.

2. 得到第一个字的输出, 具体来说就是用第一个字和其余字的注意力权重乘所有字的$v$向量, 然后求和

求和后的维度是$v$向量的维度.
示意图如下:

通过这种操作我们可以让每个$x$都产生一个$c$向量.

总体示意图如下:

变为矩阵计算

上面我们是使用了字一个个计算的, 换成矩阵也很好理解
例如下面的图, X代表一个句子, 有两行说明这个句子只有两个字, 也就是行代表字的索引, 列代表字被编码的维度.

对于注意力是这样计算的:
也就是Q乘K的转置然后除$\sqrt{d_k}$, 这是一个小trick, 经过softmax后得到注意力矩阵.

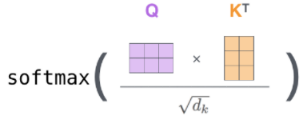
然后乘V矩阵得到输出

3. Multi-Head Attention

理解了第二部分这部分就很好理解了, 就是又增加了几个$W_Q$, $W_K$, $W_V$矩阵, 输出后感觉就像是卷积过后的多个特征图.
下图的意思就是X乘第一个$W_Q$得到$Q_0$, 以此类推.

Transformer有8个头就会得到8个Z, 如下图:

4. Padding Mask

假如是每个batch的句子不等长的情况, 那么我们需要加padding, 使得每个句子的长度变一致. 但是必须保证加的padding不会影响其他句子, 那么这就可以在padding区域加一个mask, 具体来说也就是给无效的区域加个负偏置, 因为softmax是e的对数, 假如是接近负无穷的话相应的注意力部分就接近于0

在softmax之前加一个mask矩阵, 在padding相关的区域设置为负无穷

公式如下:

$$Z_{illegal}\text{=}{Z}_{illeagl}+bia{s}_{illegal}$$$$bia{s}_{illegal}\to -\infty$$

5. 残差连接和 Layer Normalization

1. 把X经过embedding和pos_embedding后的向量加起来, 然后加上self-attention后的向量.
   
   其中$X_{embedding}\text{=}{X}_{embedding}+X_{pos}$

2. Layer Normalization

Layer Normalization 的作用是把神经网络中隐藏层归一为标准正态分布.

公式如下:
按列求均值:

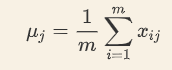
按列为单位求方差:

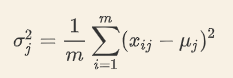
最后归一化:

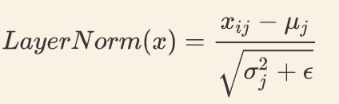
用每一列的每一个元素减去这列的均值，再除以这列的标准差，从而得到归一化后的数值，加参数是为了防止分母为0.

看一下batch_norm和layer_norm的区别:

3. 下图展示了更多细节:输入$x_1,x_2$ 经 self-attention 层之后变成$z_1^1,z_1^2,z_1^3,,,z_1^8$, $z_2^1,z_2^2,z_2^3,,,z_2^8$ ，下标是第几个字, 上标是头, 然后和输入$x_1,x_2$进行残差连接，经过 LayerNorm 后输出给全连接层。全连接层也有一个残差连接和一个 LayerNorm，最后再输出给下一个 Encoder（每个 Encoder Block 中的 FeedForward 层权重都是共享的）, 这里的共享是说$Z_1$和$Z_2$经过的feed forward的权重是一样的, 也就是说就算把Z拼接起来送入一个linear也是一样的.

这里的$Add\&Normalize$是对forward后的hidden向量和z进行相加然后通过LayerNorm. Feed forward是个两层的线性层, 中间加个relu激活.

6. 总结

1). 字向量与位置编码

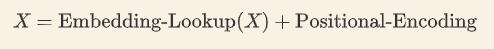
2). 自注意力机制

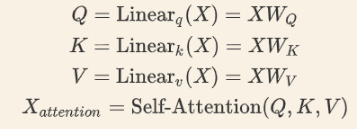
3). self-attention 残差连接与 Layer Normalization

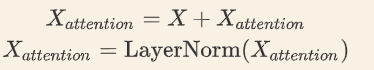
4). FeedForward，其实就是两层线性映射并用激活函数激活

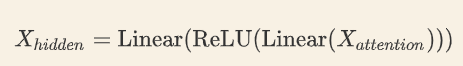
5). FeedForward 残差连接与 Layer Normalization

其中:

这里encoder会叠加, 叠加部分是一个block， 如下图：

Transformer Decoder

经过6个encoder后输出的K和V都是一样的, 然后输出到decoder中, 经过最后的add&norm后的输出再变为outputs输入到decoder中, 就完成了级联.

1. Masked Self-Attention

因为训练过程中会输入ground truth到 Decoder 中，这显然是不对的，我们需要对 Decoder 的输入进行一些处理，该处理被称为 Mask， 也就是输入一个字遮住后面的字。

举个例子，Decoder 的 ground truth 为 “ I am fine”，我们将这个句子输入到 Decoder 中，经过 WordEmbedding 和 Positional Encoding 之后，将得到的矩阵做三次线性变换$(W_Q,W_K,W_V)$。然后进行 self-attention 操作，首先通过$\frac{Q\times K^T}{\sqrt{d_k}}$得到 Scaled Scores，接下来非常关键，我们要对 Scaled Scores 进行 Mask。
参见下图：

这个图怎么看呢？ 行是索引， 列是全文，当我们输入 “I” 时，模型目前仅知道包括 “I” 在内之前所有字的信息，即 “” 和 “I” 的信息，不应该让其知道 “I” 之后词的信息。图上对应的就是道理很简单，我们做预测的时候是按照顺序一个字一个字的预测，怎么能这个字都没预测完，就已经知道后面字的信息了呢？Mask 非常简单，首先生成一个下三角全 0，上三角全为负无穷的矩阵，然后将其与 Scaled Scores 相加即可.

之后再做 softmax，就能将 - inf 变为 0，得到的这个矩阵即为每个字之间的权重

参考链接