并行CRC计算HDL代码生成工具的秘密（六字真言）_并行crc在线计算

0. 前言

CRC校验（Cyclic Redundancy Check，循环冗余校验）在数字通信领域有着非常广泛的应用，Greg Cook在其个人网站上收录了112个CRC参数模型。现代数字通信随着速率的不断增长，对CRC校验码的计算速度提出了越来越高的要求，几乎每个需要实现CRC校验编/解码的FPGA逻辑工程师或数字IC前端工程师都会接触到并行CRC计算的HDL代码编写，即在单时钟周期内完成多位输入的并行CRC计算，如下图所示：

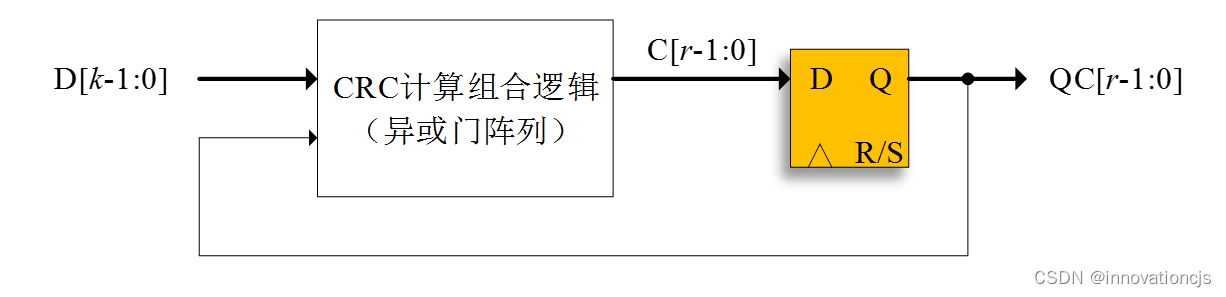
k 位输入，r 位输出的CRC计算模块，由一个(k+r)→r 的异或门组合逻辑阵列构成，此逻辑阵列的代码编写，大多数工程师都望而却步！向前辈求助？问万能的谷歌？最后基本上都会得到一份葵花宝典，没错，就是并行CRC计算的HDL（VHDL/Verilog）代码在线生成工具：

• easics
• OutputLogic
• Michael Büsch

个人比较喜欢easics的使用风格：

实际工作中，如果有并行CRC计算的HDL设计需求，当然不作他想的基于工具生成。但作为一个充满了好奇心的工程师，总是忍不住想探究这些工具背后的秘密，于是宿命般地拜读了Evgeni Stavinov（OutputLogic在线工具作者）关于此工具的文章：A Practical Parallel CRC Generation Method，还是没能透彻理解，看来还得学习理论教材，例如：Robert J.McEliece著，李斗等译，《信息论与编码理论（第二版）》，电子工业出版社。

在对CRC校验码的生成矩阵有一定理解后，回过头来再看这三个生成工具，原来仅仅是CRC生成矩阵的最简单应用，六个字即可概括：“列阵、对齐、查表”。

1. 实现（六字真言）

本文不是从理论上去分析（或证明）并行CRC计算的HDL代码生成原理，这个工作相关论文和相关教材那是干的非常专业。本文将展示的是应用教材（论文）的结论，可手工完成相关代码的编写，进而加深对CRC校验的理解（如果仅仅是为了那几行代码，用工具生成就可以了）。

本文后续以CRC8（多项式POL = 0x107， $G(x)=x^{8}+x^{2}+x^{1}+1$）为例，手工计算4-bits和8-bits并行输入的异或阵列。

1.1 列阵

要写出并行CRC计算的异或阵列表达式，最核心的是根据目标CRC多项式（次数为 r）、并行处理的位宽（k），写出对应线性分组码M(k+r, k)的典型生成矩阵G = [Ik R ]，即“列阵”，这是整个过程中唯一需要计算的步骤。

从教材可知，CRC校验码的典型生成矩阵G：

• 是一个 k 行 × (k + r) 列的矩阵；
• 左侧 Ik 是一个 k 行 × k 列的单位矩阵（对角线元素为1，其余元素为0）；
• 右侧 R 是 k 行 × r 列的矩阵，每一行是本行左侧数据的CRC校验码。

例如，CRC8、4-bits输入的典型生成矩阵G如下图：

左侧是一个k阶的独热码方阵，可直接写出。在规模较小时，右侧每行数据可直接用多项式除法求得，规模较大时可用CRC校验码工具计算获得。例如本例第一行：

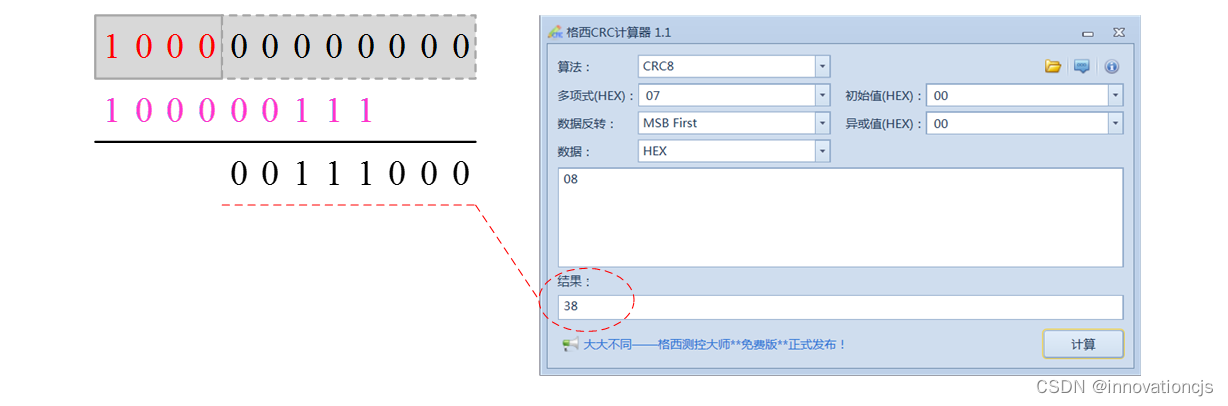
到此，本文最复杂的工作就完成了。

1.2 对齐

CRC计算基于GF(2)域的多项式长除法进行，待计算数据和计算结果需要按照多项式的幂次对齐，本文的多项式和矩阵均按降幂排列，即左侧是高位（幂次）。将输入数据 d [k-1:0]、上一周期的结果 qc [r-1:0]，本周期计算结果 c [r-1:0]与生成矩阵如下图对齐：

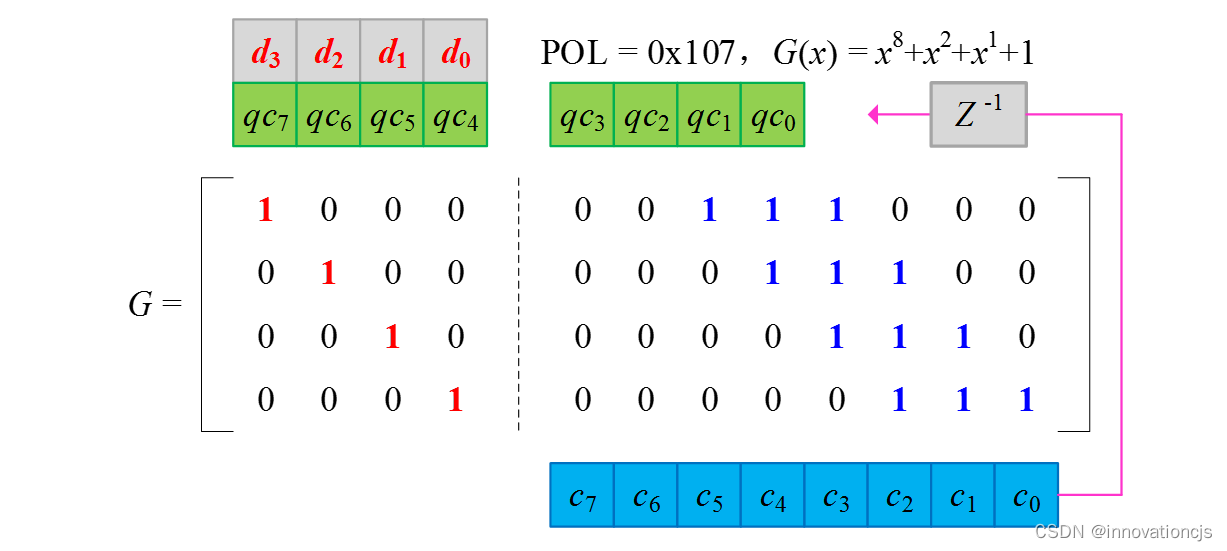
1.3 查表

在上一步已对齐的表中，以本周期待计算结果 c [r-1:0]的某位为起点，查找本位需要异或的输入元素：

• 本列指向的上一周期计算结果 qc[?]，只在并行处理位宽 k 小于CRC位宽 r 时才存在；
• 本列所有1元素往左，指向单位方阵中对应的1元素，再往上，指向对应的输入数据位 d [?]和上一周期计算结果位 qc[?]。

按上述规则，查找出本位需要异或的全部输入元素，例如，$c_{4}=d_{2} \wedge d_{3} \wedge qc_{6} \wedge qc_{7} \wedge qc_{0}$。

最终，CRC8（$G(x)=x^{8}+x^{2}+x^{1}+1$）的4-bits并行输入计算代码如下图（左侧为本文方法的结果，右侧为easics在线工具生成的结果）：

$G(x)=x^{8}+x^{2}+x^{1}+1$，8-bits并行输入CRC8计算代码生成的完整过程如下图：

1.4 并行CRC计算电路与串行CRC计算电路的关系

FPGA逻辑工程师（或数字IC前端工程师）的工作是基于数字电路来实现CRC校验码的计算，工程实践中通常分为了“并行CRC”和“串行CRC”两种计算电路。教材中如果涉及到了电路实现的介绍，通常只介绍基于串行移位寄存器实现单比特计算的“串行CRC”电路，工程师博客文章中通常将二者分别介绍，“并行CRC”电路的介绍几乎都是推荐一个在线生成工具，然后演示工具的使用效果，或简单地提一句“并行CRC计算”可将“串行CRC计算”过程迭代 k 次后展开再合并。

无论是“并行CRC计算”还是“串行CRC计算”，其依托的数学原理（或计算法则）是完全一致的，区别仅是本步计算的输入数据长度不同。二者无论在电路（或HDL代码）形式上有多大的区别，它们之间一定是可以相互转换的：

• 串行CRC计算电路 k 次迭代展开、合并、化简后，必然可得到 k 位并行CRC计算电路；
• 并行CRC计算电路删减为1位输入后，必然可得到串行CRC计算电路。

关于串行CRC计算电路到并行CRC计算电路的转换，笔者的看法是：“道理是那么个道理，但弄起来太麻烦了”，推荐参考博文：【FPGA/IC】CRC电路的Verilog实现。

并行CRC计算电路到串行CRC计算电路的转换呢？我们将本文例子的输入数据位宽修改为1-bit，如下图（实在没啥可解释的了…）：

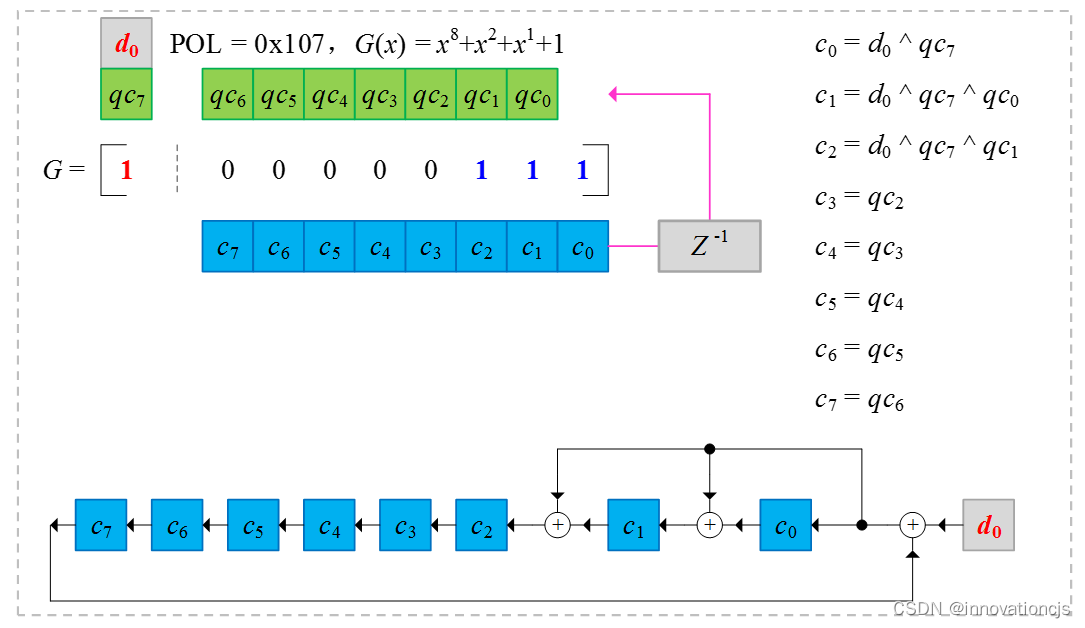
2. 本文与OutputLogic的异同

本文之并行CRC计算的异或阵列生成方法与A Practical Parallel CRC Generation Method中的方法在形式上有一定区别：

• 本文的生成矩阵对应原文的H1矩阵；
• 本文未构造原文中的H2矩阵；
• 虽未写明，但两种方法，笔者都从原理上证明过。总之，CRC计算的数学原理（运算法则）只有一种，所以无论实现形式上有什么差别，只要实现方式精确地对应了CRC计算的数学原理，则结果一定一致。

3. 本文更一般性的优化

3.1 矩阵生成（列阵）的优化

前文为便于理解，在描述求取CRC典型生成矩阵时，指明矩阵右侧监督矩阵 R 的每一行是本行左侧数据的CRC校验码，可通过多项式长除法（或利用CRC校验码计算工具）求得，这更多地是为了反映CRC典型生成矩阵的定义。

当我们想通过编制程序来生成这个矩阵时，显得效率不够高！并行处理位宽为 k 时，生成 k 行数据，我们需要 k 次的（主）循环，每次循环时，我们需要计算1个 k 位数据的CRC校验码，需要一个 k 次的（子）循环，从而我们的程序为一个 k 次双层嵌套循环结构，总循环次数为。

由于待计算数据为：0x0001、0x0002、0x0004、0x0008...，后一个数据是前一个数据左移一位（并右侧补零）。可以证明（过程略）：已知一个数（A）的CRC校验码（CRC_A），此数（A）左移一位（并右侧补零）后，新数据（B）的CRC校验码（CRC_B）等于原校验码 CRC_A 左移一位（并右侧补零）后对生成多项式 POL 求余。

数据0x...0001的CRC校验码即为生成多项式的简记式（省略最高位的1），从而我们的程序可以0x...0001的CRC校验码为初值，循环 k - 1次即可。每次循环时执行：

• 前一次的校验码左移一位，右侧补零；
• 若移出位 = 1，则移位后的校验码与 POL 的简记式按位异或的结果作为本次循环的输出；
• 若移出位 = 0，则移位后的校验码直接作为本次循环的输出。

3.2 对齐查表的优化

我们可以删掉CRC典型生成矩阵[IK R]中的 IK，只保留监督矩阵 R，根据输入数据位宽 k 与CRC校验码位宽 r 的大小关系，并优化重排 d [k-1:0]、qc [r-1:0]、c [r-1:0]与矩阵的对齐方式，可得到如下图所示的更一般的并行CRC异或阵列HDL代码生成示意图：