- 1LeetCode —— 两数相加
- 2Android技术栈(二)组件化改造,目前最稳定和高效的UI适配方案_程序组件改造适配
- 3期待一年后人工智能的飞跃:从高中生到博士的智力水平
- 4SDXL版本的基础模型和LoRA还有存在感么?(模型介绍系列DreamShaper XL1.0-综合型)_sdxl基础模型
- 5Threejs 加载模型、旋转、弹框操作_threejs点击模型弹窗
- 6GDB多线程调试:Redis的IO多线程_调试redis源码io多线程
- 7[Linux安全运维] LAMP 环境搭建保姆级教学(Apache + MySQL + PHP) ~~
- 82024年第一批跳槽的互联网人,怎么样了?_100offer为什么倒闭了
- 9【鸿蒙开发实战教程】HarmonyOS开发中的对称加密_createsymkeygenerator
- 10linux系统下,配置开机自启脚本常见的5种方法_linux自启动脚本
数据结构(c++)学习笔记--二叉搜索树_循关键码访问
赞
踩
一、概述
1.循关键码访问
- 向量、列表并不能兼顾静态查找与动态修改
| 基本结构 | 查找 | 插入/删除 |
|---|---|---|
| 无序向量 | O(n) | O(n) |
| 有序向量 | O( log n \log n logn) | O(n) |
| 无序列表 | O(n) | O(1) |
| 有序列表 | O(n) | O(n) |
-
各数据项依所持关键码 而彼此区分:call-by-KEY
-
当然,关键码之间必须同时支持比较(大小)与比对(相等)
-
数据集中的数据项,统一地表示和实现为词条(entry)形式
template struct Entry { //词条模板类
K key; V value; //关键码、数值
Entry( K k = K(), V v = V() ) : key(k), value(v) {}; //默认构造函数
Entry( Entry const & e ) : key(e.key), value(e.value) {}; //克隆
// 比较器、判等器(从此,不必严格区分词条及其对应的关键码)
bool operator< ( Entry const & e ) { return key < e.key; } //小于
bool operator> ( Entry const & e ) { return key > e.key; } //大于
bool operator==( Entry const & e ) { return key == e.key; } //等于
bool operator!=( Entry const & e ) { return key != e.key; } //不等
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
2.中序
2.1 顺序性
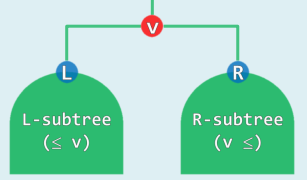
- 任一节点均不小于/不大于其左/右孩子
- 三位一体: 节点 ~ 词条 ~ 关键码
2.2 重复关键码
-
为简化起见,暂且 禁止词条的关键码重复
-
当然,这种简化
- 在应用中本非自然
- 从算法看亦无必要
2.3 单调性
- 顺序性虽只是对局部特征的刻画,却可导出BST的整体特征
- 对树高做数学归纳,不难证明BST的中序遍历序列,必然单调非降
3.接口
template<typename T> class BST : public BinTree<T> {
public: //以virtual修饰,以便派生类重写
virtual BinNodePosi<T>& search( const T & ); //查找
virtual BinNodePosi<T> insert( const T & ); //插入
virtual bool remove( const T & ); //删除
protected:
BinNodePosi<T> _hot; //命中节点的父亲
BinNodePosi<T> connect34( //3+4重构
BinNodePosi<T>, BinNodePosi<T>, BinNodePosi<T>,
BinNodePosi<T>, BinNodePosi<T>, BinNodePosi<T>, BinNodePosi<T>
);
BinNodePosi<T> rotateAt( BinNodePosi<T>); //旋转调整
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
二、算法及实现
1.查找
1.1 减而治之
-
从根节点出发,逐步地缩小查找范围,直到发现目标(成功),或抵达空树(失败)
-
对照中序遍历序列可见,整个过程可视作是在 仿效有序向量的二分查找
template<typename T> BinNodePosi<T> & BST<T>::search( const T & e ) {
if ( !_root || e == _root->data ) //空树,或恰在树根命中
{ _hot = NULL; return _root; }
for ( _hot = _root; ; ) { //否则,自顶而下
BinNodePosi<T>& v = ( e < _hot->data ) ? _hot->lc : _hot->rc; //深入一层
if ( !v || e == v->data ) return v;
_hot = v; //一旦命中或抵达叶子,随即返回
} //返回目标节点位置的引用,以便后续插入、删除操作
} //无论命中或失败,_hot均指向v之父亲(v是根时,hot为NULL)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
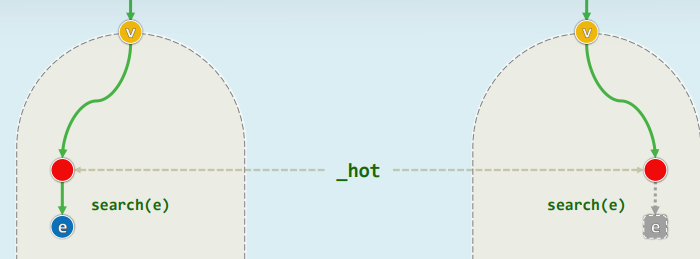
1.2 返回的引用值
- 查找成功时,指向一个关键码为e且真实存在的节点
- 失败时,指向最后一次试图转向的空节点NULL——随后可视需要进行修改,此时,不妨假想地将该空节点转换为一个数值为e的哨兵节点
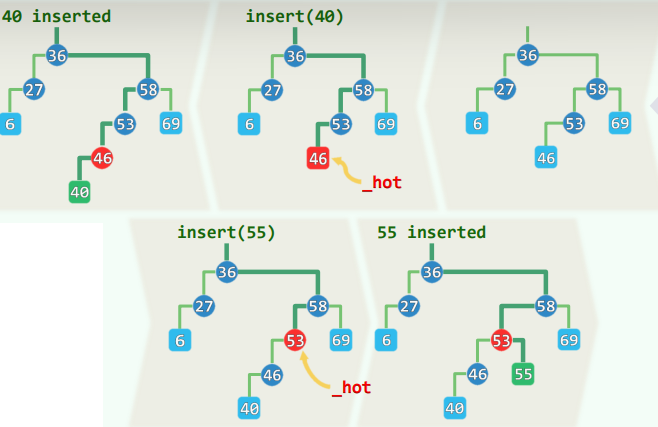
2.插入
-
先借助search(e) 确定插入位置及方向
-
若e尚不存在,则再 将新节点作为叶子插入
- _hot为新节点的父亲
- v = search(e)为_hot对新孩子的引用
-
于是,只需令_hot通过v指向新节点
template <typename T> BinNodePosi<T> BST<T>::insert( const T & e ) {
BinNodePosi<T> & x = search( e ); //查找目标(留意_hot的设置)
if ( ! x ) { //既禁止雷同元素,故仅在查找失败时才实施插入操作
x = new BinNode<T>( e, _hot ); //在x处创建新节点,以_hot为父亲
_size++; updateHeightAbove( x ); //更新全树规模,更新x及其历代祖先的高度
}
return x; //无论e是否存在于原树中,至此总有x->data == e
} //验证:对于首个节点插入之类的边界情况,均可正确处置
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 时间主要消耗于search(e)和updateHeightAbove(x);均线性正比于x的深度,不超过树高
3.删除
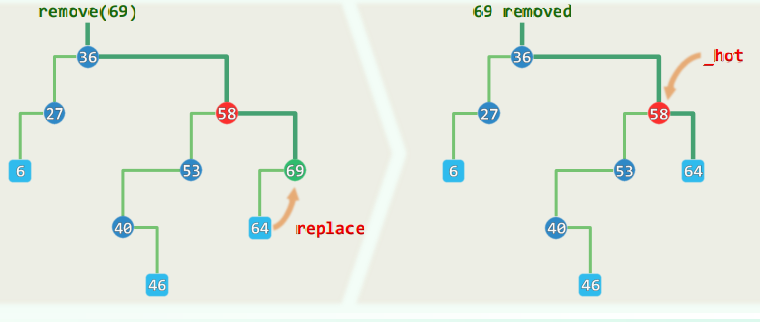
3.1 单分支
-
若*x(69)的某一子树为空,则可将其替换为另一子树(64)(可能亦为空)
-
验证:如此操作之后,二叉搜索树的拓扑结构依然完整;顺序性依然满足
3.2 双分支
-
若:x(36)左、右孩子并存,则调用BinNode::succ()找到x的直接后继 (必无左孩子);交换x(36)与*w(40)
-
于是问题转化为删除w,可按前一情况处理
-
尽管顺序性在中途曾一度不合 但最终必将重新恢复
3.3 算法
template<typename T> bool BST<T>::remove( const T & e ) { BinNodePosi<T> & x = search( e ); //定位目标节点 if ( !x ) return false; //确认目标存在(此时_hot为x的父亲) removeAt( x, _hot ); //分两大类情况实施删除,更新全树规模 _size--; //更新全树规模 updateHeightAbove( _hot ); //更新_hot及其历代祖先的高度 return true; } //删除成功与否,由返回值指示 template<typename T> static BinNodePosi<T> removeAt( BinNodePosi & x, BinNodePosi & hot ) { BinNodePosi w = x; //实际被摘除的节点,初值同x BinNodePosi succ = NULL; //实际被删除节点的接替者 //单分支 if ( ! HasLChild( *x ) ) succ = x = x->rc; //左子树为空 else if ( ! HasRChild( *x ) ) succ = x = x->lc; //右子树为空 //此类情况仅需O(1)时间 //双分支 else {//若x的左、右子树并存,则 w = w->succ(); swap( x->data, w->data ); //令*x与其后继*w互换数据 BinNodePosi u = w->parent; //原问题即转化为,摘除非二度的节点w ( u == x ? u->rc : u->lc ) = succ = w->rc; //兼顾特殊情况:u可能就是x } //时间主要消耗于succ(),正比于x的高度——更精确地,search()与succ()总共不过O(h) hot = w->parent; //记录实际被删除节点的父亲 if ( succ ) succ->parent = hot; //将被删除节点的接替者与hot相联 release( w->data ); release( w ); return succ; //释放被摘除节点,返回接替者 }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 累计O(h)时间:search()、updateHeightAbove();还有removeAt()中可能调用的succ()
三、平衡
1.期望值高
1.1 树高:最坏情况与平均情况
-
由以上的实现与分析,BST主要接口search()、insert()和remove()的运行时间,在最坏情况下,均线性正比于其高度O(h)
-
若不能有效地控制树高,就无法体现出BST相对于向量、列表等数据结构的明显优势
-
比如在最(较)坏情况下,二叉搜索树可能彻底地(接近地)退化为列表,此时的性能不仅没有提高,而且因为结构更为复杂,反而会(在常系数意义上)下降
1.2 随机生成:n个词条{ e 1 , e 2 , . . . , e n e_1,e_2,...,e_n e1,e2,...,en}按随机排列σ={ e i 1 , e i 2 , . . . , e i n e_{i_1},e_{i_2},...,e_{i_n} ei1,ei2,...,ein}依次插入
- 若假设各排列出现的概率均等(1/n!),则BST平均高度为 Θ ( log n ) Θ(\log n) Θ(logn)
- 的确,多数实际应用中的BST总体上都是如此生成和演化的,即便计入remove(),也可通过随机使用succ()和pred(),避免逐渐倾侧的趋势
1.3 随机组成:n个互异节点,在遵守顺序性的前提下,随机确定拓扑联接关系
-
由n个互异节点随机组成的BST,若共计S(n)棵,则有 S ( n ) = ∑ k = 1 n S ( k − 1 ) ⋅ S ( n − k ) = c a t a l a n ( n ) = ( 2 n ) ! / ( ( n + 1 ) ! ⋅ n ! ) S(n)=\sum_{k=1}^{n}S(k-1)·S(n-k)=catalan(n)=(2n)!/((n+1)! · n!) S(n)=∑k=1nS(k−1)⋅S(n−k)=catalan(n)=(2n)!/((n+1)!⋅n!)
-
假定所有BST等概率地出现,则其平均高度为 Θ ( n ) Θ(\sqrt{n}) Θ(n )
-
在Huffman编码之类的应用中,二叉树(尽管还不是BST)的确是逐渐拼合而成的
1.4 logn vs. sqrt(n)
- 理想随机在实际中绝难出现:局部性、关联性、(分段)单调性、(近似)周期性、… 较高甚至极高的BST频繁出现,不足为怪;平衡化处理很有必要
2.理想与渐进
2.1 理想平衡
- 节点数目固定时,兄弟子树的高度越接近(平衡),全树也将倾向于更低
- 由n个节点组成的二叉树,高度不致低于 ⌊ log 2 n ⌋ \lfloor \log_2 n\rfloor ⌊log2n⌋——达到这一下界时,称作理想平衡
- 大致相当于完全树甚至满树:叶节点只能出现于最底部的两层——条件过于苛刻
2.2 渐近平衡
- 理想平衡出现的概率极低、维护的成本过高,故须适当地放松标准
- 退一步海阔天空:高度渐近地不超过O( log n \log n logn),即可接受
- 渐近平衡的BST,简称平衡二叉搜索树(BBST)
3.等价交换
3.1 等价BST
- 上下可变:联接关系不尽相同,承袭关系可能颠倒
- 左右不乱:中序遍历序列完全一致,全局单调非降
3.2 限制条件 + 局部性
- 各种BBST都可视作BST的某一子集,相应地满足精心设计的限制条件
- 单次动态修改操作后,至多O( log n \log n logn)处局部不再满足限制条件(可能相继违反,未必同时)
- 可在O( log n \log n logn)时间内,使这些局部(以至全树)重新满足
3.3 等价变换 + 旋转调整:序齿不序爵
-
刚刚失衡的BST,必可迅速转换为一棵等价的BBST——为此,只需O( log n \log n logn)甚至O(1)次旋转
-
zig和zag:仅涉及常数个节点,只需调整其间的联接关系;均属于局部的基本操作
-
调整之后:v/c深度加/减1,子(全)树高度的变化幅度,上下差异不超过1
-
实际上,经过不超过O(n)次旋转,等价的BST均可相互转化
四、AVL树
1.渐近平衡
1.1 平衡因子
- 平衡因子(Balance Factor): b a l F a c ( v ) = h e i g h t ( l v ( v ) ) − h e i g h t ( r c ( v ) ) balFac(v)=height(lv(v))-height(rc(v)) balFac(v)=height(lv(v))−height(rc(v))
- AVL树未必理想平衡,但必然渐近平衡
1.2 AVL = 渐近平衡
- 高度为h的AVL树,至少包含S(h)=fib(h+3)-1个节点
- S ( h ) = 1 + S ( h − 1 ) + s ( h − 2 ) S(h)=1+S(h-1)+s(h-2) S(h)=1+S(h−1)+s(h−2)
- S ( h ) + 1 = [ S ( h − 1 ) + 1 ] + S ( h − 2 ) + 1 S(h)+1=[S(h-1)+1]+S(h-2)+1 S(h)+1=[S(h−1)+1]+S(h−2)+1
- f i b ( h + 3 ) = f i b ( h + 2 ) + f i b ( h + 1 ) fib(h+3)=fib(h+2)+fib(h+1) fib(h+3)=fib(h+2)+fib(h+1)
- 反过来,由n个节点构成的AVL树,高度不超过O( log n \log n logn)
1.3 最小生成树(Fibonaccian Tree)
- 高度为h,规模恰为S(h)=fib(h+3)-1的AVL树
- 最“瘦”的、“临界”的AVL树
2.重平衡
2.1 接口
#define Balanced(x) ( stature( (x).lc ) == stature( (x).rc ) ) //理想平衡
#define BalFac(x) (stature( (x).lc ) - stature( (x).rc ) ) //平衡因子
#define AvlBalanced(x) ( ( -2 < BalFac(x) ) && (BalFac(x) < 2 ) ) //AVL平衡条件
template class AVL : public BST { //由BST派生
public: //BST::search()等接口,可直接沿用
BinNodePosi insert( const T & ); //插入(重写)
bool remove( const T & ); //删除(重写)
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
2.2 失衡
- 按BST规则动态操作之后,AVL平衡性可能破坏 (当然,只涉及到祖先)
- 插入:从祖父开始,每个祖先都有可能失衡,且可能同时失衡!
- 删除:从父亲开始,每个祖先都有可能失衡,但至多一个!
2.3 重平衡
- 恢复平衡须借助等价变换
- 局部性:所有的旋转都在局部进行(每次只需O(1)时间)
- 快速性:在每一深度只需检查并旋转至多一次(共O( log n \log n logn)次)
3.插入
3.1 单旋:黄色方块恰好存在其一
- 同时可有多个失衡节点,最低者g不低于x的祖父
- g经单旋调整后复衡,子树高度复原
- 更高祖先也必平衡,全树复衡
3.2 双旋
- 同时可有多个失衡节点,最低者g不低于x的祖父
- g经单旋调整后复衡,子树高度复原
- 更高祖先也必平衡,全树复衡
3.3 代码
template <typename T> BinNodePosi<T> AVL<T>::insert( const T & e ) {
BinNodePosi<T> & x = search( e ); if ( x ) return x; //若目标尚不存在
BinNodePosi<T> xx = x = new BinNode<T>( e, _hot ); _size++; //则创建新节点
// 此时,若x的父亲_hot增高,则祖父有可能失衡
for ( BinNodePosi<T> g = _hot; g; g = g->parent ) //从_hot起,逐层检查各代祖先g
if ( ! AvlBalanced( *g ) ) { //一旦发现g失衡,则通过调整恢复平衡
FromParentTo(*g) = rotateAt( tallerChild( tallerChild( g ) ) );
break; //局部子树复衡后,高度必然复原;其祖先亦必如此,故调整结束
} else //否则(g仍平衡)
updateHeight( g ); //只需更新其高度(注意:即便g未失衡,高度亦可能增加)
return xx; //返回新节点位置
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
4.删除
4.1 单旋:黄色方块至少存在其一;红色方块可有可无
- 同时至多一个失衡节点g, 首个可能就是x的父亲_hot
- 复衡后子树高度未必复原更高祖先仍可能随之失衡
- 失衡可能持续向上传播最多需做O( log n \log n logn)次调整
4.2 双旋
- 同时至多一个失衡节点g, 首个可能就是x的父亲_hot
- 复衡后子树高度不能复原更高祖先仍可能随之失衡
- 失衡可能持续向上传播最多需做O( log n \log n logn)次调整
4.3 代码
template<typename T> bool AVL<T>::remove( const T & e ) {
BinNodePosi<T> & x = search( e ); if ( !x ) return false; //若目标的确存在
removeAt( x, _hot ); _size--; //则在按BST规则删除之后,_hot及祖先均有可能失衡
// 以下,从_hot出发逐层向上,依次检查各代祖先g
for ( BinNodePosi<T> g = _hot; g; g = g->parent ) {
if ( ! AvlBalanced( *g ) ) //一旦发现g失衡,则通过调整恢复平衡
g = FromParentTo( *g ) = rotateAt( tallerChild( tallerChild( g ) ) );
updateHeight( g ); //更新高度(注意:即便g未曾失衡或已恢复平衡,高度均可能降低)
} //可能需做过Ω(logn)次调整;无论是否做过调整,全树高度均可能下降
return true; //删除成功
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
5.(3+4)-重构
5.1 返璞归真
-
设g为最低的失衡节点,沿最长分支考察祖孙三代:g ~ p ~ v,按中序遍历次序,重命名为:a < b < c
-
它们总共拥有四棵子树(或为空) 按中序遍历次序,重命名为: T 0 < T 1 < T 2 < T 3 T_0 < T_1 < T_2 < T_3 T0<T1<T2<T3
-
将原先以g为根的子树S,替换为一棵新子树S’
-
等价变换,保持中序遍历次序: T 0 < a < T 1 < b < T 2 < c < T 3 T_0 <a< T_1 <b< T_2 <c< T_3 T0<a<T1<b<T2<c<T3
5.2 代码
template BinNodePosi BST::connect34(
BinNodePosi a, BinNodePosi b, BinNodePosi c,
BinNodePosi T0, BinNodePosi T1, BinNodePosi T2, BinNodePosi T3
){
a->lc = T0; if (T0) T0->parent = a;
a->rc = T1; if (T1) T1->parent = a;
c->lc = T2; if (T2) T2->parent = c;
c->rc = T3; if (T3) T3->parent = c;
b->lc = a; a->parent = b; b->rc = c; c->parent = b;
updateHeight(a); updateHeight(c); updateHeight(b); return b;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
5.3 统一调整
template<typename T> BinNodePosi<T> BST<T>::rotateAt( BinNodePosi v ) { BinNodePosi p = v->parent, g = p->parent; if ( IsLChild( * p ) ) //zig if ( IsLChild( * v ) ) { //zig-zig p->parent = g->parent; //向上联接 return connect34( v, p, g, v->lc, v->rc, p->rc, g->rc ); } else { //zig-zag v->parent = g->parent; //向上联接 return connect34( p, v, g, p->lc, v->lc, v->rc, g->rc ); } else if ( IsLChild( * v ) ) { //zig-zig p->parent = g->parent; //向上联接 return connect34( v, p, g, v->lc, v->rc, p->rc, g->rc ); } else { //zig-zag v->parent = g->parent; //向上联接 return connect34( p, v, g, p->lc, v->lc, v->rc, g->rc ); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18

5.4 AVL:综合评价
- 优点:无论查找、插入或删除,最坏情况下的复杂度均为O( log n \log n logn),O(n)的存储空间
- 缺点:借助高度或平衡因子,为此需改造元素结构,或额外封装 实测复杂度与理论值尚有差距
- 插入/删除后的旋转,成本不菲
- 删除操作后,最多需旋转 Ω ( log n ) Ω(\log n) Ω(logn)次(Knuth:平均仅0.21次)
- 若需频繁进行插入/删除操作,未免得不偿失
- 单次动态调整后,全树拓扑结构的变化量可能高达 Ω ( log n ) Ω(\log n) Ω(logn)