矩阵求导和分解_对ax求x导数

1、向量对向量的导数

设A为mn的矩阵，x为n1的列向量，y为m1的列向量，那么对于矩阵运算y=Ax有

基本的向量求导公式有：

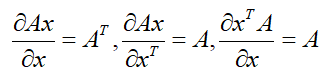
2、标量对向量的导数

A为nn的矩阵，x为n1的列向量，对于标量y=x^TAx对向量x的求导结果为：

3、正交阵和对称阵

3.1正交阵

若n阶矩阵A满足A^TA=I，称A为正交阵。其充要条件是A的列向量都是单位向量，且两两正交。
A为正交阵，X为向量，则Ax称作正交变换，正交变换不改变向量长度，即
(Ax)^T*Ax=x^TA^T*Ax=x^Tx

3.2特征值和特征向量

A是n阶矩阵，若数λ和n维非0向量x满足Ax=λx，那么数λ称为A的特征值，x称为A对应特征值的特征向量。
特征值的性质：
设n阶矩阵A=(a_ij)的特征值为λ₁，λ₂，…,λ_n则
λ₁+λ₂+…+λ_n=a₁₁+a₂₂+…+a_nn
λ₁λ₂…λ_n=|A|
矩阵A主对角线的元素和， 称作矩阵A的迹。

若矩阵A的特征值互不相等，那么其对应的特征向量也线性无关。
实对称阵不同特征值的特征向量正交，证明如下：

那么对于对称阵A，必有正交阵P=(u₁,u₂,…,u_n),其中u_i为A的特征值λ_i对应的特征向量，则有

白化处理：
对于观测数据x,对称阵xx^T的对角矩阵D和正交阵U，那么有xx^T=UDU^T
令x^*=UD^-0.5U^T*x,称x的白化处理，可得
x^*x^*T=I,即白化后的x^*为正交矩阵，x的列向量正交，即x的特征不相关。

白化处理的作用就是消除特征之间的相关性。

3.3正定阵

对于n阶方阵A，若任意n阶向量x，都有x^TAx>0,则称A是正定阵。
若条件变成x^TAx≥0，则称A为半正定矩阵。
类似的还有负定阵，半负定阵。
（x^TAx)维度→（1* n* n* n* n1）=（11）
给定任意m*n的矩阵A，A^TA一定是半正定方阵。

对称阵A为正定阵的判定：
A的特征值都为正
A的顺序主子式都大于零

4、QR分解

对于m*n的列满秩矩阵A，必有：
A_m*n=Q_m*n*R_n*n
其中，Q^TQ=I，即Q为列正交矩阵，R为非奇异上三角矩阵，当要求R对角元素为正时，该分解唯一。
QR分解可用于求矩阵A的逆和特征值。
当A为方阵时
A^-1=R^-1Q^-1=R^-1Q^T
只要求出上三角矩阵R的逆矩阵，就可以得到A的逆矩阵。

求特征值：
A=Q₁*R₁，A₁=Q₁^TAQ₁=Q₁^TQ₁R₁Q₁=R₁Q₁
…
A_k=Q_k*R_k，A_k+1=R_kQ_k
随着变换次数的增加，上三角矩阵R的元素值逐渐接近零，最后得到对角矩阵A_k，其对角元素值即为元素A的特征值。
A_k=diag{λ₁，λ₂，λ₃,…,λ_n}

5、奇异值分解（SVD）

假设A是一个m*n阶实矩阵，则存在一个分解使得：
A_m*n=U_m*mΣ_m*nV^T_n*n

通常将奇异值从大到小的排列得到唯一的半正定m*n阶对角矩阵Σ。

—Σ的对角元素为称为奇异值，是A^TA的特征值λ_i的二次开方值。
—U的列(columns)组成一套的对A的正交“输入”基向量，这些向量是方阵AA^T的特征向量。
—V的列(columns)组成一套对A的正交"输出"的基向量。这些向量是方阵A^TA的特征向量。

其中假设m>n，u_i维度为m×1，v_i维度为1×n，SVD相当于我们把一个矩阵分解成若干个特征的权重之和，因为σ_i是从大到小排列的，我们可以认为最大奇异值σ₁对应的u₁v₁是矩阵A的最重要特征。
主成分分析(PCA)就是选取前K个特征值和特征向量u,v来大致表示原矩阵A。

6、广义矩阵逆