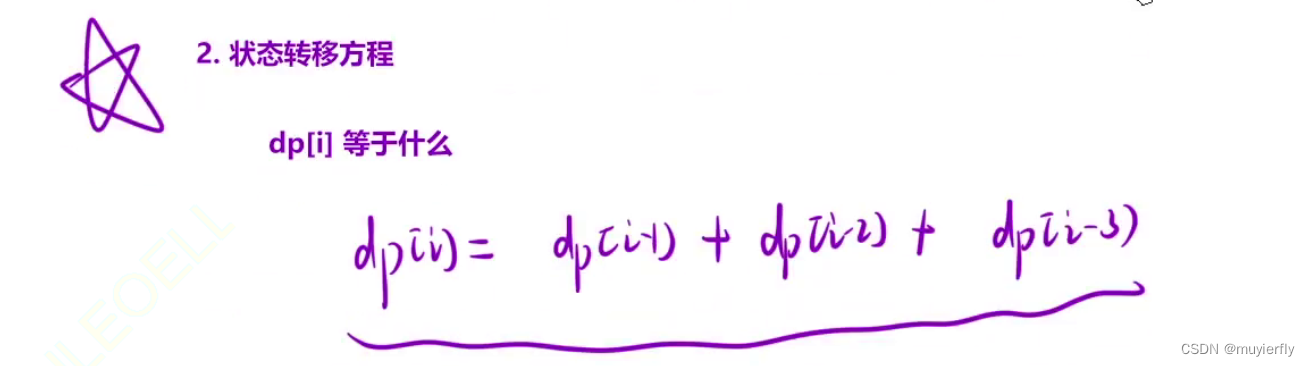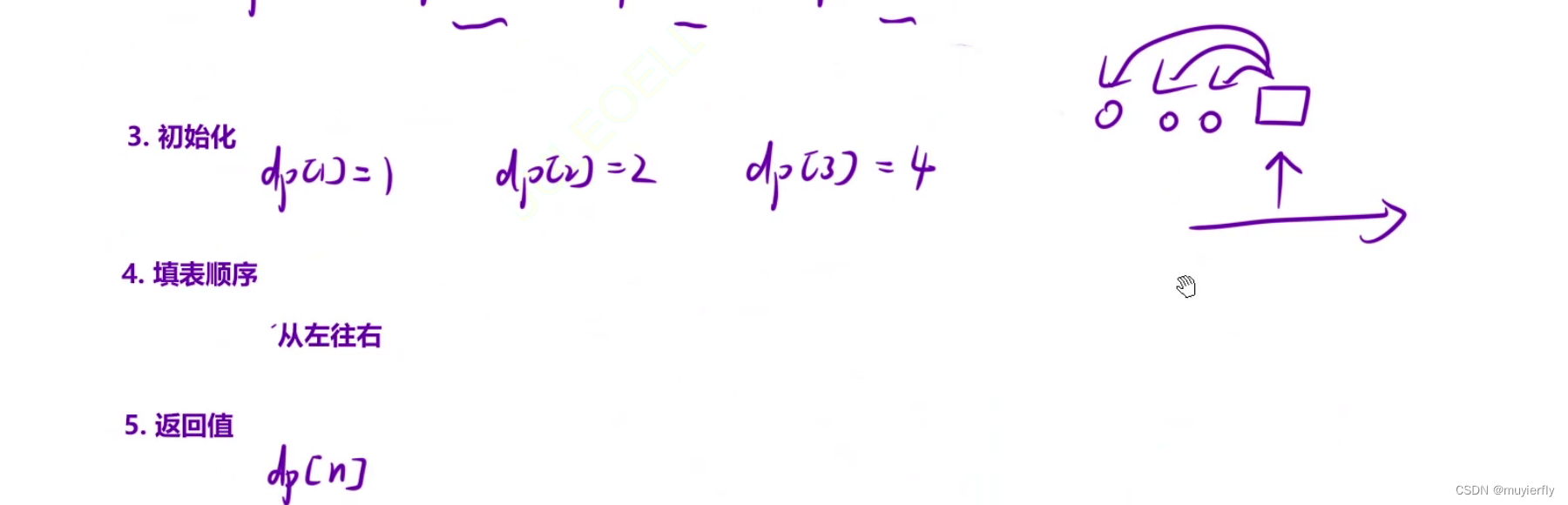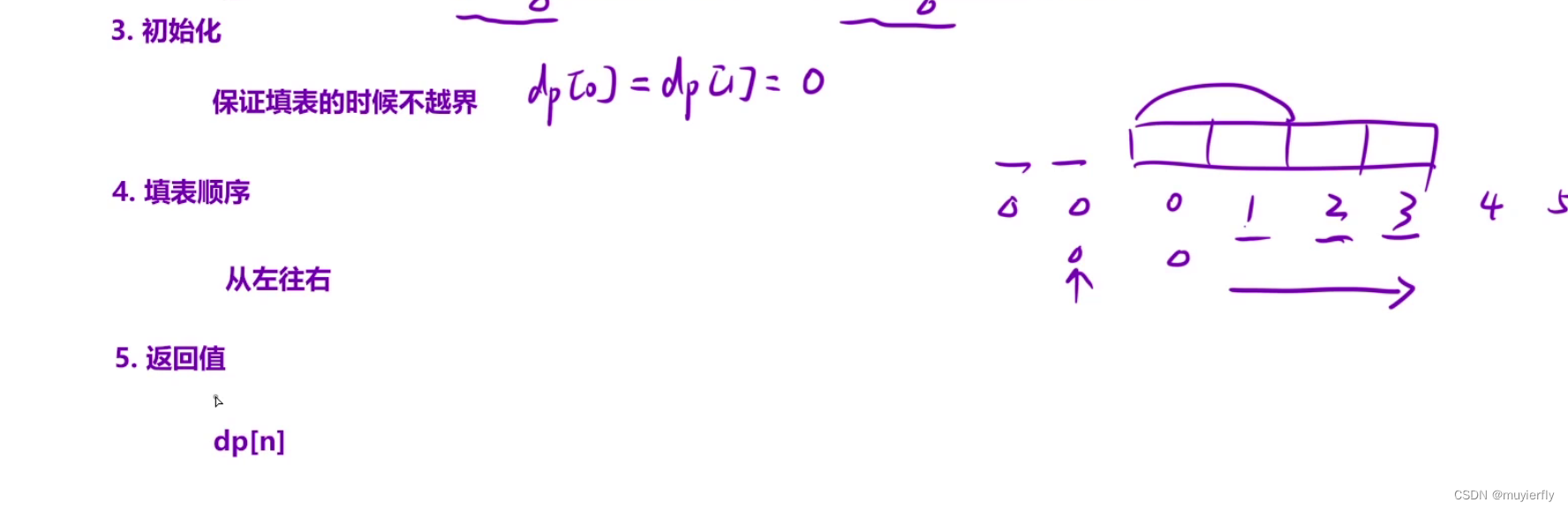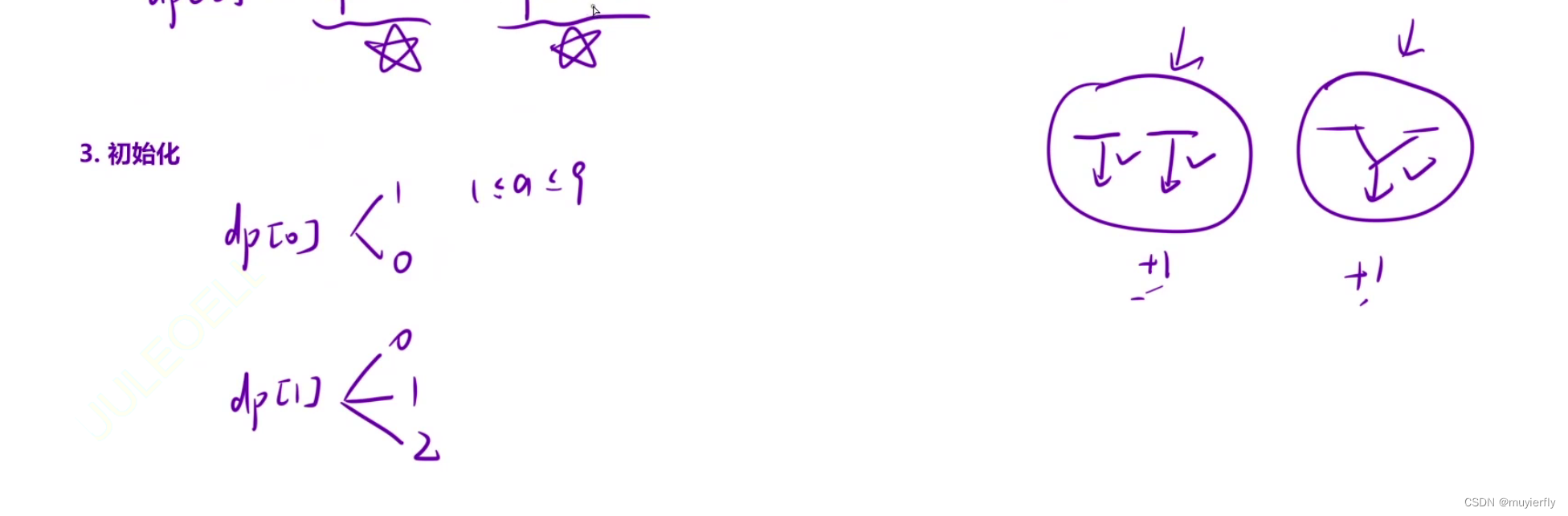爱喝兽奶帝天荒

这个屌丝很懒，什么也没留下！

热门标签

18.动态规划之斐波那契数列模型1

作者：爱喝兽奶帝天荒 | 2024-07-14 02:51:03

踩

18.动态规划之斐波那契数列模型1

1.第N个斐波那契数

1137. 第 N 个泰波那契数 - 力扣（LeetCode）

做题流程

1. 状态表示：

这道题可以【根据题目的要求】直接定义出状态表示：

dp[i] 表示：第 i 个泰波那契数的值。

2. 状态转移方程：

题目已经非常贴心的告诉我们了：

dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]

3. 初始化：

从我们的递推公式可以看出， dp[i] 在 i = 0 以及 i = 1 的时候是没有办法进⾏推导的，因

为 dp[-2] 或 dp[-1] 不是⼀个有效的数据。

因此我们需要在填表之前，将 0, 1, 2 位置的值初始化。题⽬中已经告诉我们 dp[0] = 0,

dp[1] = dp[2] = 1 。

4. 填表顺序：

毫⽆疑问是「从左往右」。

5. 返回值：

应该返回 dp[n] 的值。


class Solution {
    public int tribonacci(int n) {
        // 1. 创建 dp 表
        // 2. 初始化
        // 3. 填表
        // 4. 返回结果
 
        // 处理边界情况
        if (n == 0)
            return 0;
        if (n == 1 || n == 2)
            return 1;
        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = dp[2] = 1;
        for (int i = 3; i <= n; i++)
            dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
        return dp[n];
    }
}

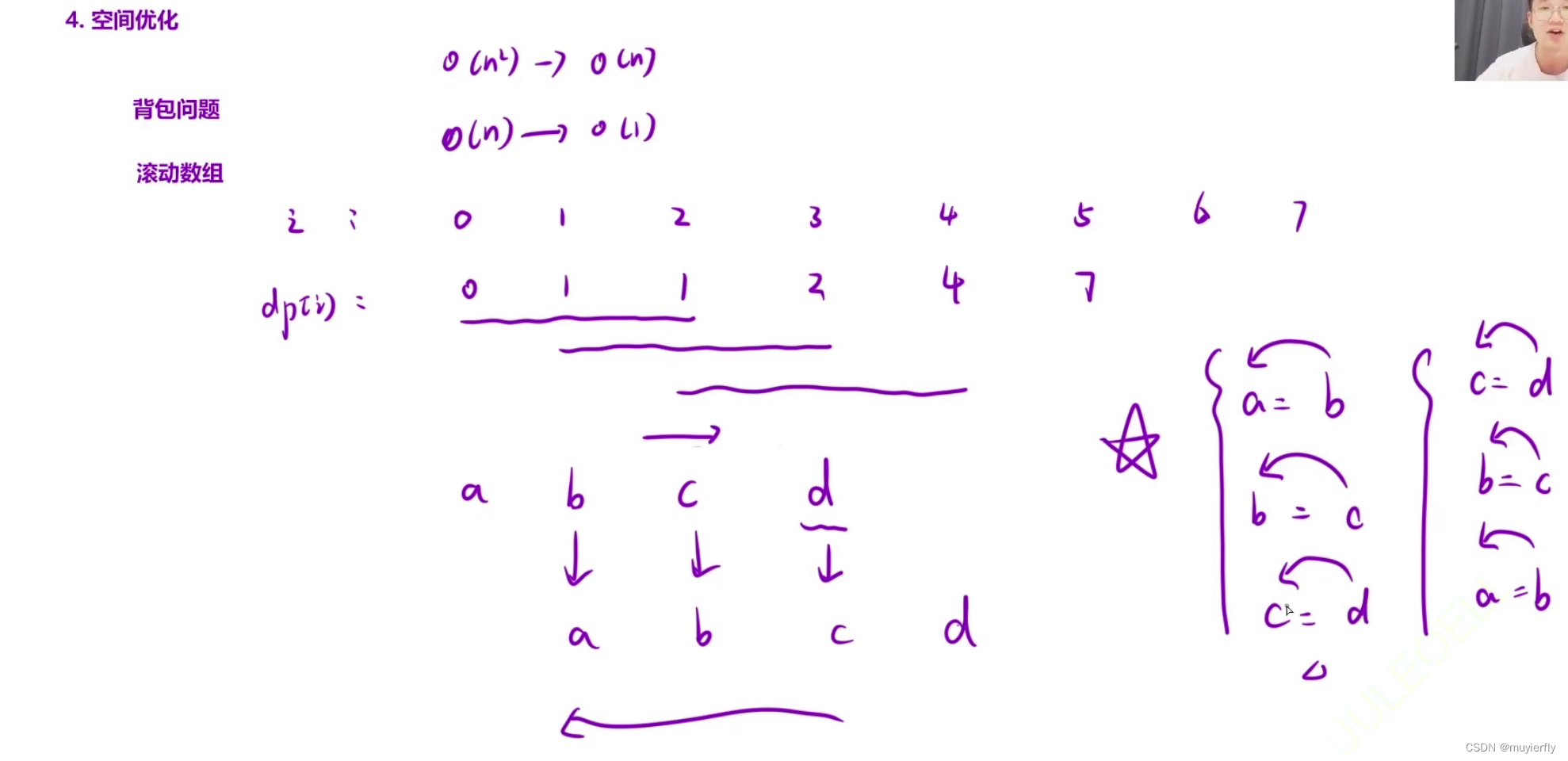
空间优化


class Solution {
    public int tribonacci(int n) {
        if (n == 0)
            return 0;
        if (n == 1 || n == 2)
            return 1;
        int a = 0, b = 1, c = 1, d = 0;
        for (int i = 3; i <= n; i++) {
            d = a + b + c;
            a = b;
            b = c;
            c = d;
        }
        return d;
    }
}

2.三步问题

面试题 08.01. 三步问题 - 力扣（LeetCode）

算法思路

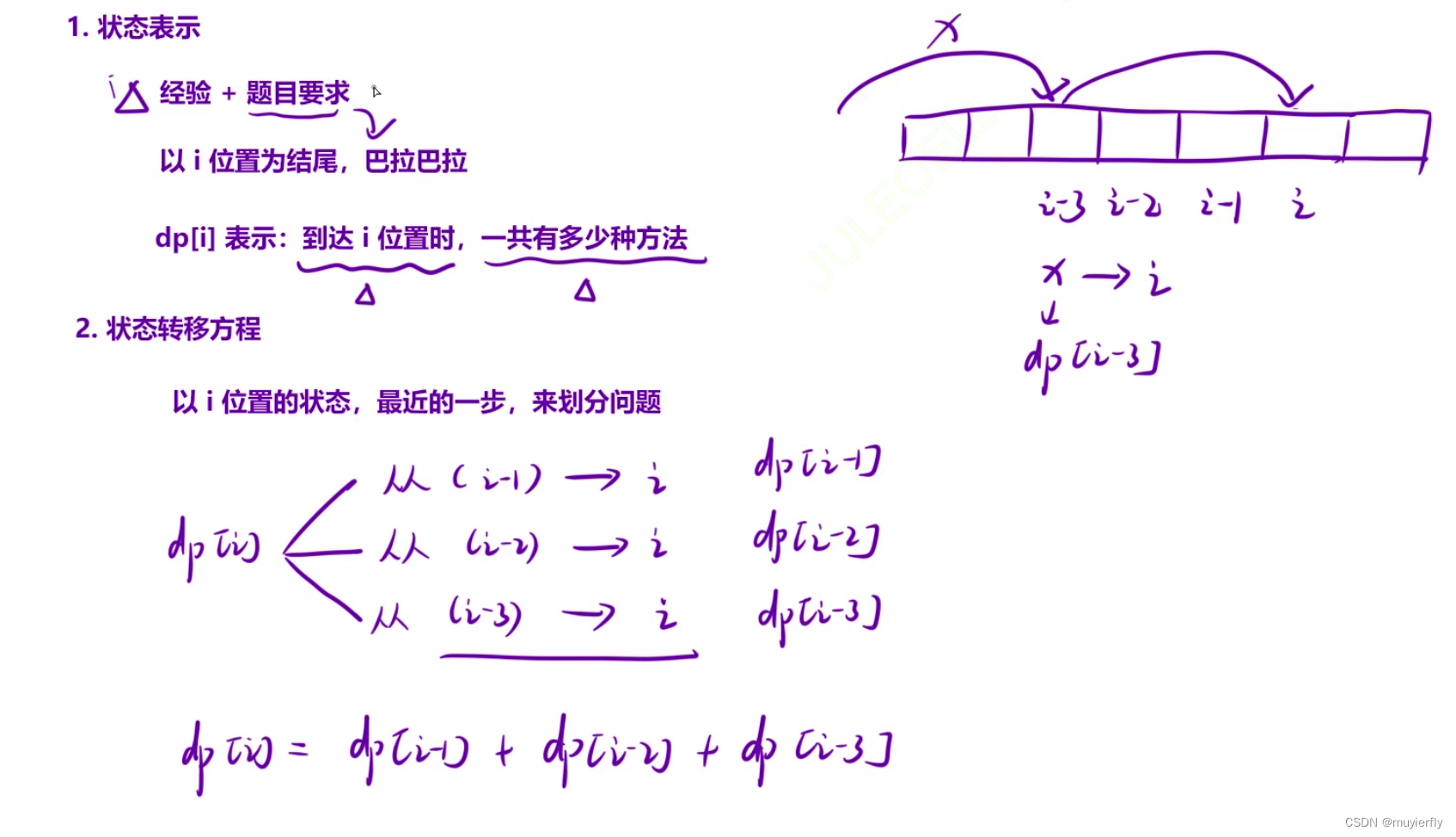
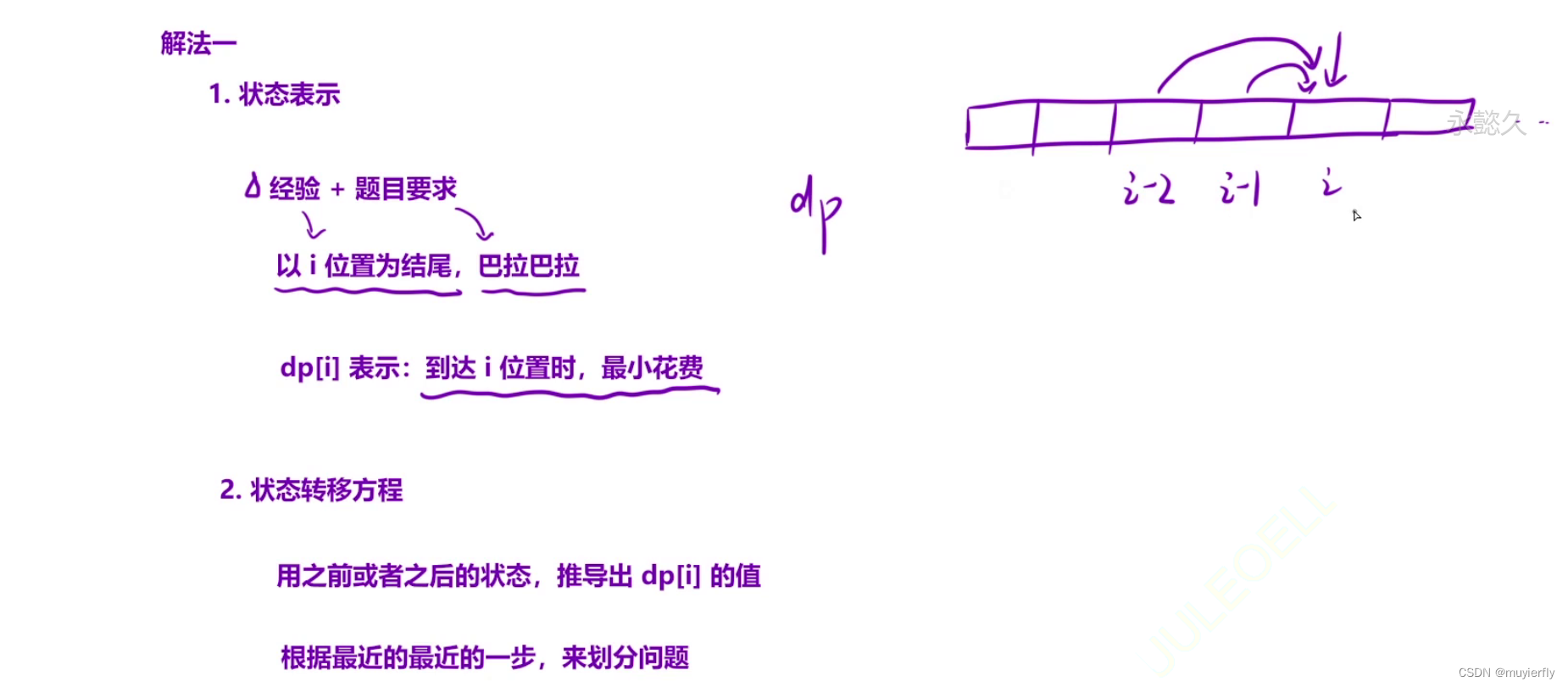
1. 状态表示

这道题可以根据「经验 + 题⽬要求」直接定义出状态表⽰：

dp[i] 表⽰：到达 i 位置时，⼀共有多少种⽅法。

2. 状态转移⽅程

以 i 位置状态的最近的⼀步，来分情况讨论：

如果 dp[i] 表⽰⼩孩上第 i 阶楼梯的所有⽅式，那么它应该等于所有上⼀步的⽅式之和：

i. 上⼀步上⼀级台阶， dp[i] += dp[i - 1] ；

ii. 上⼀步上两级台阶， dp[i] += dp[i - 2] ；

iii. 上⼀步上三级台阶， dp[i] += dp[i - 3] ；

综上所述， dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3] 。

需要注意的是，这道题⽬说，由于结果可能很⼤，需要对结果取模。

在计算的时候，三个值全部加起来再取模，即 (dp[i - 1] + dp[i - 2] + dp[i - 3])

% MOD 是不可取的，同学们可以试验⼀下， n 取题⽬范围内最⼤值时，⽹站会报错 signed

integer overflow 。

对于这类需要取模的问题，我们每计算⼀次（两个数相加/乘等），都需要取⼀次模。否则，万⼀

发⽣了溢出，我们的答案就错了。

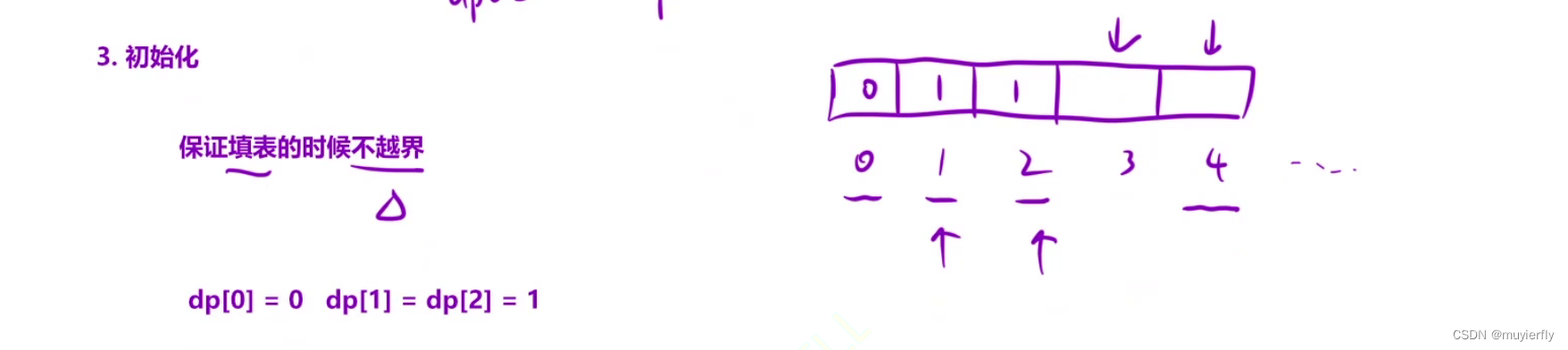
3. 初始化

从我们的递推公式可以看出， dp[i] 在 i = 0, i = 1 以及 i = 2 的时候是没有办法进⾏

推导的，因为 dp[-3] dp[-2] 或 dp[-1] 不是⼀个有效的数据。

因此我们需要在填表之前，将 1, 2, 3 位置的值初始化。

根据题意， dp[1] = 1, dp[2] = 2, dp[3] = 4 。

4. 填表顺序

毫⽆疑问是「从左往右」。

5. 返回值

应该返回 dp[n] 的值。


class Solution {
    public int waysToStep(int n) {
        // 1. 创建 dp 表
        // 2. 初始化
        // 3. 填表
        // 4. 返回值
        int MOD = (int) 1e9 + 7;
 
        // 处理⼀下边界情况
        if (n == 1 || n == 2)
            return n;
        if (n == 3)
            return 4;
 
        int[] dp = new int[n + 1];
        dp[1] = 1;
        dp[2] = 2;
        dp[3] = 4;
        for (int i = 4; i <= n; i++)
            dp[i] = ((dp[i - 1] + dp[i - 2]) % MOD + dp[i - 3]) % MOD;
        return dp[n];
    }
}

3.最小花费爬楼梯

746. 使用最小花费爬楼梯 - 力扣（LeetCode）

题目解析

算法思路

解法一：


class Solution {
    public int minCostClimbingStairs(int[] cost) {
        // 1. 创建 dp 表
        // 2. 初始化
        // 3. 填表
        // 4. 返回值
        int n = cost.length;
        int[] dp = new int[n + 1];
        for (int i = 2; i <= n; i++)
            dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        return dp[n];
    }
}

解法二：


class Solution {
    public int minCostClimbingStairs(int[] cost) {
        // 1. 创建 dp 表
        // 2. 初始化
        // 3. 填表
        // 4. 返回值
        int n = cost.length;
        int[] dp = new int[n];
        dp[n - 1] = cost[n - 1];
        dp[n - 2] = cost[n - 2];
        for (int i = n - 3; i >= 0; i--)
            dp[i] = Math.min(dp[i + 1], dp[i + 2]) + cost[i];
        return Math.min(dp[0], dp[1]);
    }
}

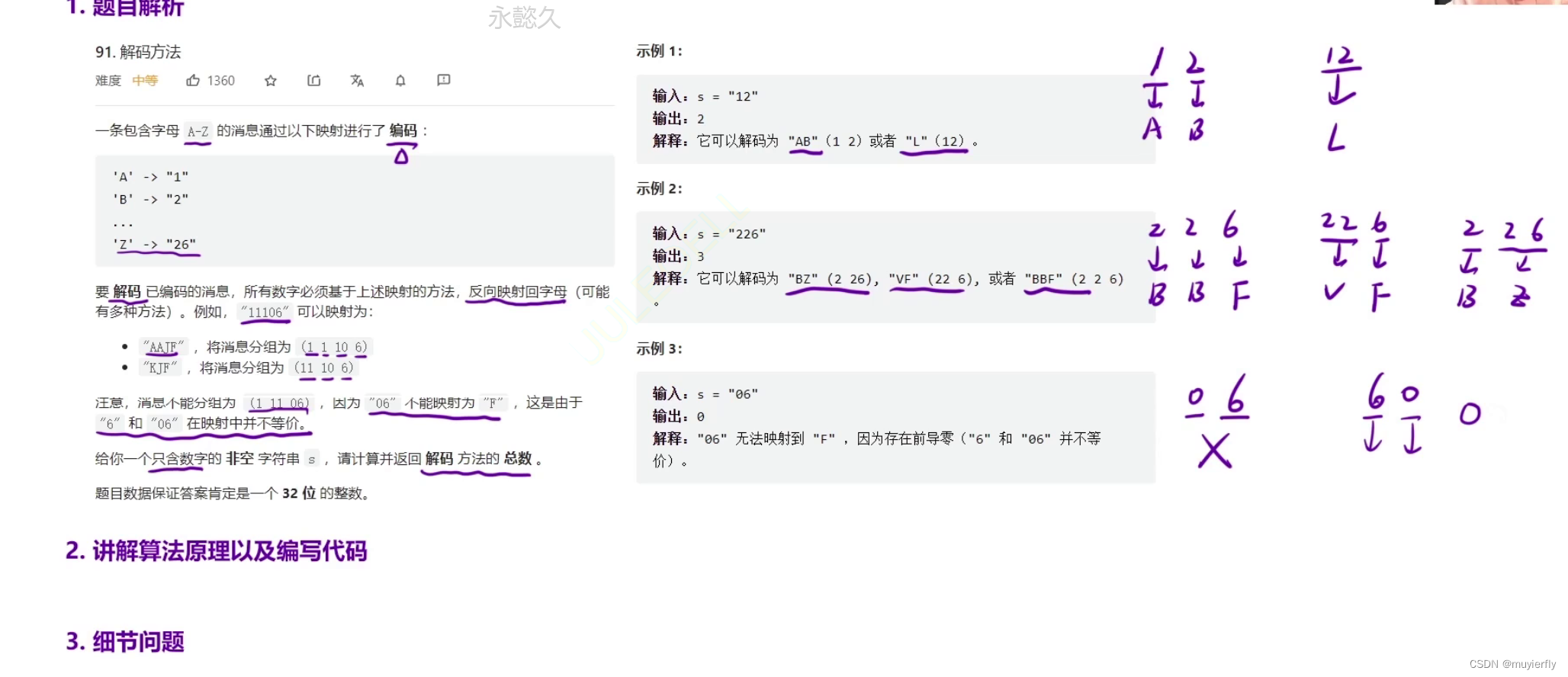
4.解码方法

91. 解码方法 - 力扣（LeetCode）

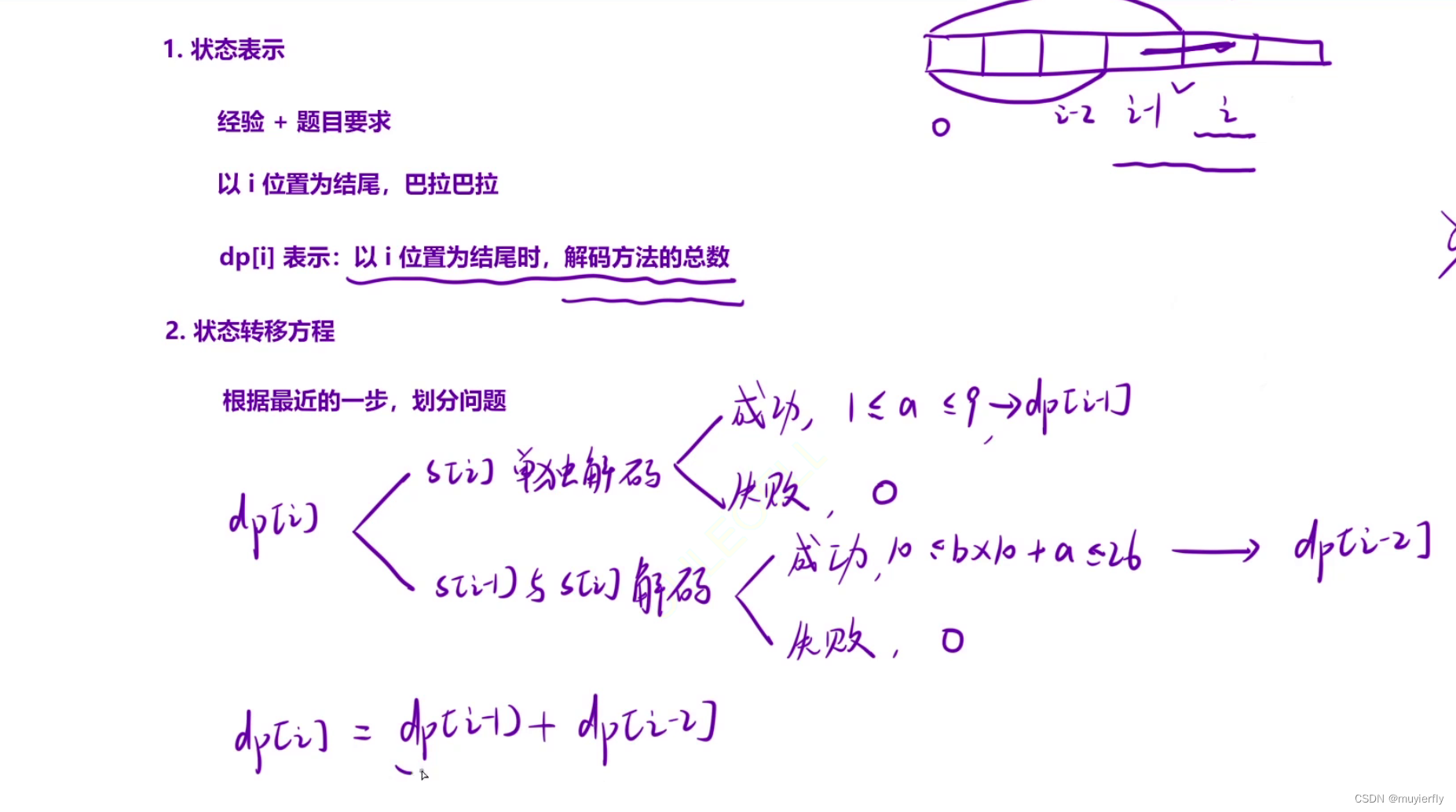
算法思路


class Solution {
    public int numDecodings(String ss) {
        // 1. 创建 dp 表
        // 2. 初始化
        // 3. 填表
        // 4. 返回值
        int n = ss.length();
        char[] s = ss.toCharArray();
        int[] dp = new int[n];
        if (s[0] != '0')
            dp[0] = 1; // 初始化第⼀个位置
        if (n == 1)
            return dp[0]; // 处理边界情况
        // 初始化第⼆个位置
        if (s[1] != '0' && s[0] != '0')
            dp[1] += 1;
        int t = (s[0] - '0') * 10 + s[1] - '0';
        if (t >= 10 && t <= 26)
            dp[1] += 1;
        for (int i = 2; i < n; i++) {
            // 先处理第⼀种情况
            if (s[i] != '0')
                dp[i] += dp[i - 1];
            // 处理第⼆种情况
            int tt = (s[i - 1] - '0') * 10 + s[i] - '0';
            if (tt >= 10 && tt <= 26)
                dp[i] += dp[i - 2];
        }
        return dp[n - 1];
    }
}

细节问题


ass Solution {
    public int numDecodings(String ss) {
        // 1. 创建 dp 表
        // 2. 初始化
        // 3. 填表
        // 4. 返回值
        int n = ss.length();
        char[] s = ss.toCharArray();
        int[] dp = new int[n + 1];
        dp[0] = 1; // 保证后续填表是正确的
        if (s[1 - 1] != '0')
            dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            // 先处理第⼀种情况
            if (s[i - 1] != '0')
                dp[i] += dp[i - 1];
            // 处理第⼆种情况
            int tt = (s[i - 2] - '0') * 10 + s[i - 1] - '0';
            if (tt >= 10 && tt <= 26)
                dp[i] += dp[i - 2];
        }
        return dp[n];
    }
}

本文内容由网友自发贡献，转载请注明出处：【wpsshop博客】