DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model翻译

摘要

我们提出了 DeepSeek-V2，一种强大的混合专家 (MoE) 语言模型，具有训练经济、推理高效的特点。它包含 236B 总参数，其中每个 token 激活 21B，支持 128K token 的上下文长度。DeepSeek-V2 采用了包括 Multi-head Latent Attention (MLA) 和 DeepSeekMoE 在内的创新架构。MLA 通过将key-value (KV) 缓存显著压缩为潜在向量来保证高效推理，而 DeepSeekMoE 通过稀疏计算以经济的成本训练强大的模型。与 DeepSeek 67B 相比，DeepSeek-V2 实现了显著增强的性能，同时节省了 42.5% 的训练成本、减少了 93.3% 的 KV 缓存、并将最大生成吞吐量提升至 5.76 倍。我们在由 8.1T token组成的高质量多源语料库上对 DeepSeek-V2 进行了预训练，并进一步执行有监督微调 (SFT) 和强化学习 (RL) 以充分发挥其潜力。评估结果表明，即使只有 21B 激活参数，DeepSeek-V2 及其chat版本仍然在开源模型中实现了顶级性能。模型checkpoint可在 https://github.com/deepseek-ai/DeepSeek-V2 上找到。

1.介绍

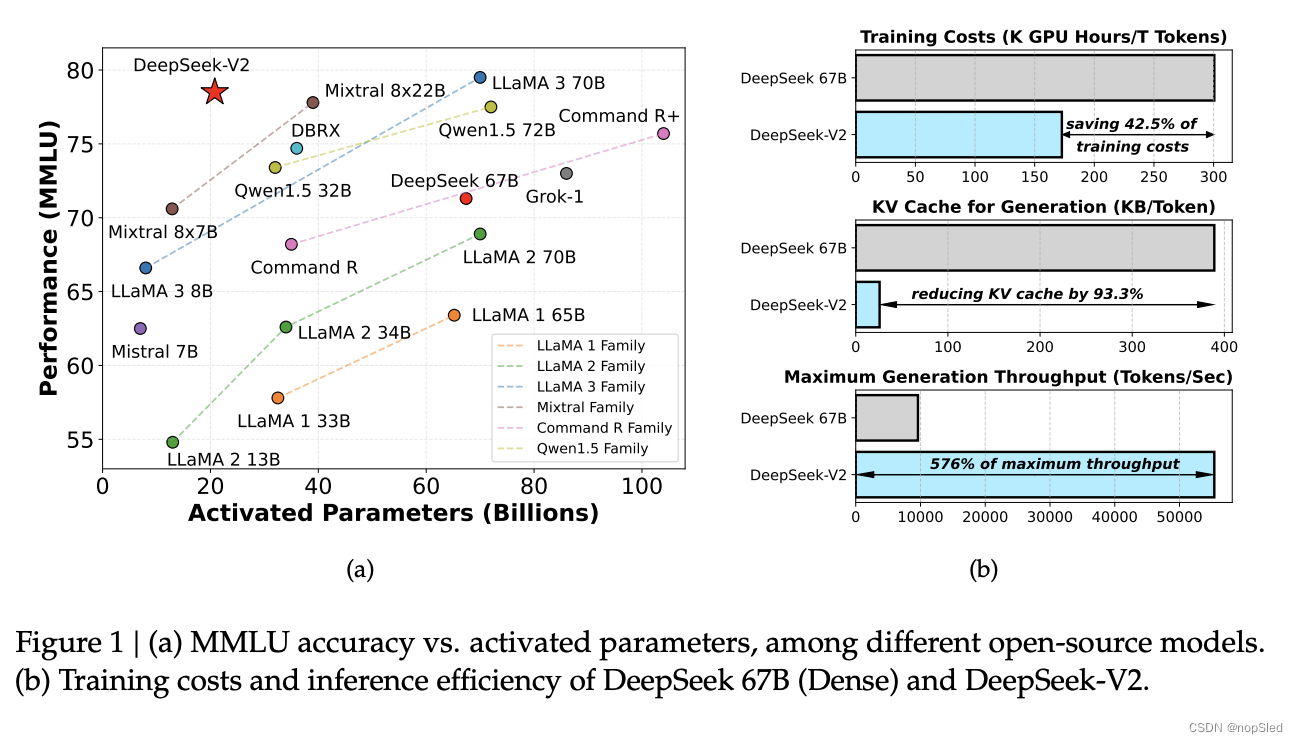
　　过去几年，大型语言模型 (LLM) 经历了快速发展，让我们看到了通用人工智能 (AGI) 的曙光。一般来说，LLM 的智能会随着参数数量的增加而提高，从而能够在各种任务中展现出新兴的能力。然而，这种改进是以更大的训练计算资源和潜在的推理吞吐量下降为代价的。这些限制带来了重大挑战，阻碍了 LLM 的广泛采用和使用。为了解决这个问题，我们推出了 DeepSeek-V2，这是一个强大的开源混合专家 (MoE) 语言模型，其特点是通过创新的 Transformer 架构实现经济的训练和高效的推理。它总共配备了 236B 个参数，其中每个 token 激活 21B，并支持 128K 个 token 的上下文长度。
　　我们利用提出的 Multi-head Latent Attention (MLA) 和 DeepSeekMoE 优化了 Transformer 框架中的注意力模块和前馈网络 (FFN)。（1）在注意力机制中，多头注意力 (MHA) 的key-value (KV) 缓存对 LLM 的推理效率造成了重大阻碍。人们已经探索了各种方法来解决这个问题，包括group-query注意力 (GQA) 和multi-query注意力 (MQA)。然而，这些方法在试图减少 KV 缓存时往往会损害性能。为了兼顾两全其美，我们引入了 MLA，一种配备低秩key-value联合压缩的注意力机制。从经验上看，MLA 与 MHA 相比实现了相当的性能，同时显著减少了推理过程中的 KV 缓存，从而提高了推理效率。(2) 对于前馈网络 (FFN)，我们遵循 DeepSeekMoE 架构，该架构采用细粒度专家分割和共享专家隔离，以实现更高效的专业化潜力。与 GShard 等传统 MoE 架构相比，DeepSeekMoE 架构表现出巨大优势，使我们能够以经济的成本训练出强大的模型。由于我们在训练过程中采用专家并行，我们还设计了补充机制来控制通信开销并确保负载平衡。通过结合这两种技术，DeepSeek-V2 同时具有强大的性能（图 1(a)）、经济的训练成本和高效的推理吞吐量（图 1(b)）。
　　我们构建了一个由 8.1T token组成的高质量、多源预训练语料库。与 DeepSeek 67B（我们之前的版本）中使用的语料库相比，这个语料库的数据量更大，尤其是中文数据，数据质量更高。我们首先在完整的预训练语料库上对 DeepSeek-V2 进行预训练。然后，我们收集了 1.5M 个对话会话，涵盖数学、代码、写作、推理、安全等各个领域，对 DeepSeek-V2 Chat（SFT）进行有监督微调（SFT）。最后，我们遵循 DeepSeekMath 使用 Group Relative Policy Optimization (GRPO) 使模型进一步与人类偏好保持一致并生成 DeepSeek-V2 Chat（RL）。
　　我们对英文和中文的大量基准测试集进行了 DeepSeek-V2 评估，并将其与具有代表性的开源模型进行了比较。评估结果表明，即便在只有 21B 激活参数的情况下，DeepSeek-V2 仍然取得了开源模型中顶级的性能，成为最强的开源 MoE 语言模型。图 1(a) 突出显示了在 MMLU 上，DeepSeek-V2 仅使用少量激活参数就取得了顶级性能。此外，如图 1(b) 所示，与 DeepSeek 的 67B 相比，DeepSeek-V2 节省了 42.5% 的训练成本，减少了 93.3% 的 KV 缓存，并将最大生成吞吐量提高了 5.76 倍。我们还在开源基准测试集上评估了 DeepSeek-V2 Chat (SFT) 和 DeepSeek-V2 Chat (RL)。值得一提的是，DeepSeek-V2 Chat (RL) 在 AlpacaEval 2.0 上获得了 38.9 的长度控制胜率，在 MT-Bench 上获得了 8.97 的总分，在 AlignBench 上获得了 7.91 的总分。英文开源对话评测表明，DeepSeek-V2 Chat (RL) 在开源聊天模型中拥有顶级性能。此外，AlignBench 的评测表明，在中文中，DeepSeek-V2 Chat (RL) 的表现优于所有开源模型，甚至超越了大多数闭源模型。
　　为了方便大家对 MLA 和 DeepSeekMoE 进行进一步的研究和开发，我们还向开源社区发布了搭载 MLA 和 DeepSeekMoE 的较小模型 DeepSeek-V2-Lite，共计 15.7B 个参数，其中每个 token 激活 2.4B 个参数。DeepSeek-V2-Lite 的详细描述可参见附录 B。
　　在本文的其余部分，我们首先详细描述了 DeepSeek-V2 的模型架构（第 2 节）。随后，我们介绍了我们的预训练工作，包括训练数据构建、超参数设置、基础设置、长上下文扩展以及模型性能和效率的评估（第 3 节）。接下来，我们展示了我们在协同方面的努力，包括监督微调 (SFT)、强化学习 (RL)、评估结果和其他讨论（第 4 节）。最后，我们总结结论，讨论 DeepSeek-V2 当前的局限性，并概述我们未来的工作（第 5 节）。

2.Architecture

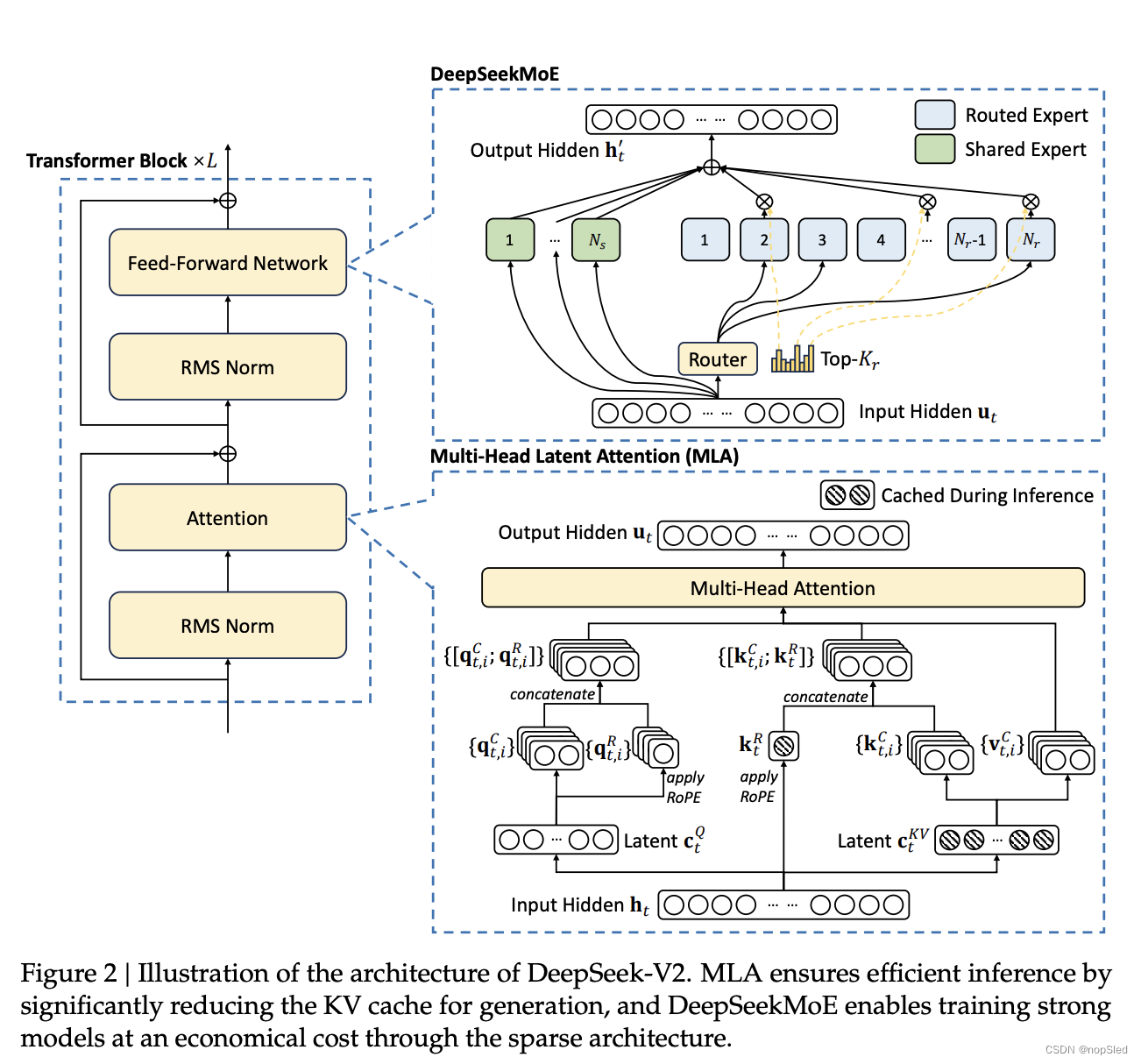
　　总体来说，DeepSeek-V2 还是 Transformer 架构，每个 Transformer 模块由一个注意力模块和一个前馈网络（FFN）组成。不过，无论是注意力模块还是 FFN，我们都设计并采用了创新的架构。对于注意力模版，我们设计了 MLA，利用低秩key-value联合压缩以消除推理时key-value缓存的瓶颈，从而支持高效推理。对于 FFN，我们采用了 DeepSeekMoE 架构，这是一种高性能的 MoE 架构，能够以经济的成本训练出强大的模型。DeepSeek-V2 的架构如图 2 所示，本节我们将介绍 MLA 和 DeepSeekMoE 的细节。对于其他微小的细节（例如，FFN 中的层归一化和激活函数），除非特别说明，DeepSeek-V2 都遵循 DeepSeek 67B 的设置。

2.1 Multi-Head Latent Attention: Boosting Inference Efficiency

传统的 Transformer 模型通常采用多头注意力机制（MHA），但在生成过程中，其较大的key-value（KV）缓存会成为限制推理效率的瓶颈。为了减少 KV 缓存，提出了multi-query注意力机制（MQA）和group-query注意力机制（GQA）。它们需要的 KV 缓存量级较小，但性能却不如 MHA（我们在附录 D.1 中给出了 MHA、GQA 和 MQA 的比较）。
　　对于 DeepSeek-V2，我们设计了一种创新的注意力机制，称为 Multi-head Latent Attention (MLA)。MLA 配备了低秩key-value联合压缩，性能优于 MHA，但所需的 KV 缓存量明显较少。我们在下面介绍了它的架构，并在附录 D.2 中提供了 MLA 和 MHA 之间的比较。

2.1.1 Preliminaries: Standard Multi-Head Attention

我们首先介绍标准的 MHA 机制作为背景。令 $d$ 为 embedding 维度，$n_h$ 为注意力头的数量，$d_h$ 为每个注意力头的维度，${\text{h}}_t\in {\mathbb{R}}^d$ 为注意力层上第 $t$ 个 token 的注意力输入。标准 MHA 首先通过三个矩阵 $W^Q,W^K,W^V\in {\mathbb{R}}^{d_h{n}_h\times d}$ 分别产生 ${\text{q}}_t,{\text{k}}_t,{\text{v}}_t\in {\mathbb{R}}^{d_h{n}_h}$：
$${\text{q}}_t=W^Q{\text{h}}_t,\text{\hspace{1em}(1)}$$
$${\text{k}}_t=W^K{\text{h}}_t,\text{\hspace{1em}(2)}$$
$${\text{v}}_t=W^V{\text{h}}_t,\text{\hspace{1em}(3)}$$
　　然后，${\text{q}}_t,{\text{k}}_t,{\text{v}}_t$ 将被切成 $n_h$ 个头，以进行多头注意力计算：
$$[{\text{q}}_{t,1};{\text{q}}_{t,2};...;{\text{q}}_{t,n_h}]={\text{q}}_t,\text{\hspace{1em}(4)}$$
$$[{\text{k}}_{t,1};{\text{k}}_{t,2};...;{\text{k}}_{t,n_h}]={\text{k}}_t,\text{\hspace{1em}(5)}$$
$$[{\text{v}}_{t,1};{\text{v}}_{t,2};...;{\text{v}}_{t,n_h}]={\text{v}}_t,\text{\hspace{1em}(6)}$$
$${\text{o}}_{t,i}=\sum _{j=1}^{t}Softma{x}_j(\frac{{\text{q}}_{t,i}^T{\text{k}}_{j,i}}{\sqrt{d_h}}){\text{v}}_{j,i},\text{\hspace{1em}(7)}$$
$${\text{u}}_t=W^O[{\text{o}}_{t,1};{\text{o}}_{t,2};...;{\text{o}}_{o_{t,n_h}}],\text{\hspace{1em}(8)}$$
其中 ${\text{q}}_{t,i},{\text{k}}_{t,i},{\text{v}}_{t,i}\in {\mathbb{R}}^{d_h}$ 分别表示第 $i$ 个注意力头的 query、key 和 value；$W^O\in {\mathbb{R}}^{d\times d_h{n}_h}$ 表示输出投影矩阵。在推理过程中，需要缓存所有 key 和 value 以加速推理，因此 MHA 需要为每个 token 缓存 $2n_h{d}_{h}l$ 个元素。在模型部署中，这种繁重的 KV 缓存是限制最大batch大小和序列长度的一大瓶颈。

2.1.2 Low-Rank Key-Value Joint Compression

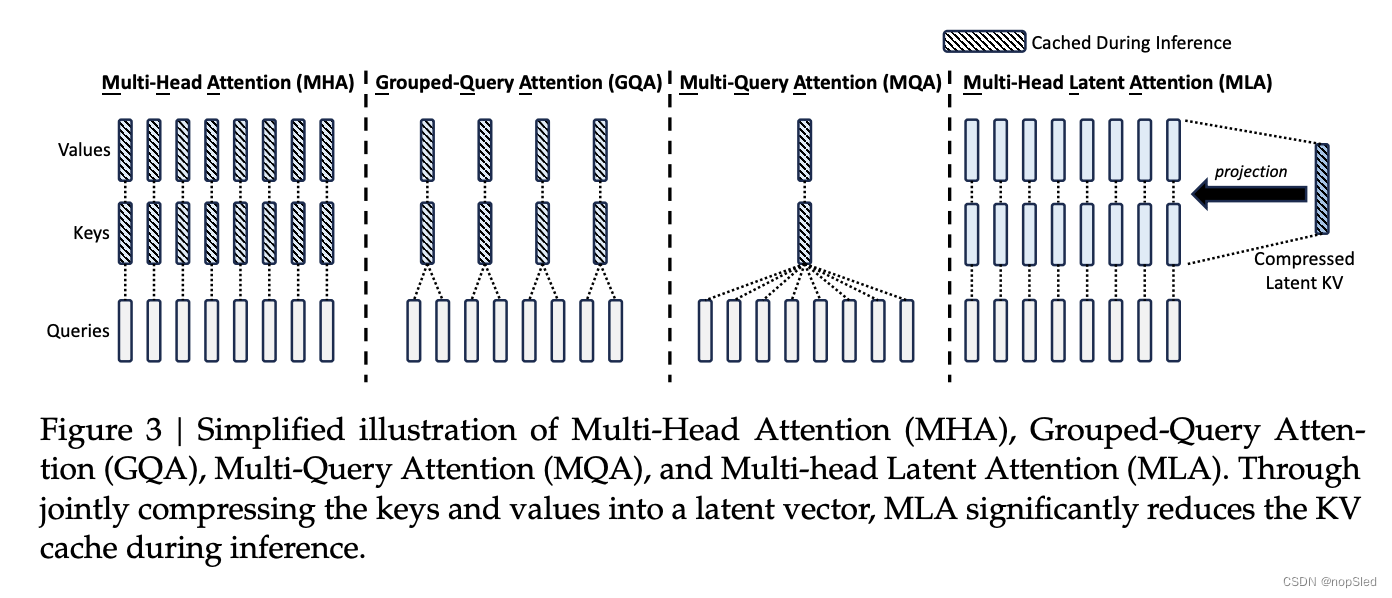
　　MLA的核心是对key和value进行低秩联合压缩，以减少KV缓存：
$${\text{c}}_t^{KV}=W^{DKV}{\text{h}}_t,\text{\hspace{1em}(9)}$$
$${\text{k}}_t^C=W^{UK}{\text{c}}_t^{KV},\text{\hspace{1em}(10)}$$
$${\text{v}}_t^C=W^{UV}{\text{c}}_t^{KV},\text{\hspace{1em}(11)}$$
其中 ${\text{c}}_t^{KV}\in {\mathbb{R}}^{d_c}$ 是key和value的压缩潜在向量；$d_c(\ll d_h{n}_h)$ 表示 KV 压缩维度；$W^{DKV}\in {\mathbb{R}}^{d_c\times d}$ 是下投影矩阵；$W^{UK},W^{UV}\in {\mathbb{R}}^{d_h{n}_h\times d_c}$ 分别是key和value的上投影矩阵。在推理过程中，MLA 只需要缓存 $c_t^{KV}$，因此其 KV 缓存只有 $d_{c}l$ 个元素，其中 $l$ 表示层数。此外，在推理过程中，由于$W^{UV}$可以被吸收到$W^O$中，我们甚至不需要计算出用于注意的key和value。图3直观地说明了MLA中的KV联合压缩如何减少KV缓存。
　　下面是对query进行低秩压缩，即使它不能减少KV缓存：
$${\text{c}}_t^Q=W^{DQ}{\text{h}}_t,\text{\hspace{1em}(12)}$$
$${\text{q}}_t^C=W^{UQ}{\text{c}}_t^Q,\text{\hspace{1em}(13)}$$
其中 $c_t^Q\in {\mathbb{R}}^{d_c^{\prime }}$ 是query的压缩潜在向量；$d_c^{\prime }(\ll d_h{n}_h)$ 表示query压缩维度；$W^{DQ}\in {\mathbb{R}}^{d_c^{\prime }\times d},W^{UQ}\in {\mathbb{R}}^{d_h{n}_h\times d_c^{\prime }}$ 分别是query的下投影和上投影矩阵。

2.1.3 Decoupled Rotary Position Embedding

　　继 DeepSeek 67B 之后，我们打算在 DeepSeek-V2 中使用旋转位置嵌入 (RoPE)。然而，RoPE 与低秩 KV 压缩不兼容。具体来说，RoPE 对key和value都是位置敏感的。如果我们对key ${\text{k}}_t^C$ 应用 RoPE，则等式 10 中的 $W^{UK}$ 将与位置敏感的 RoPE 矩阵耦合。这样，$W^{UK}$ 在推理过程中就无法再被吸收到 $W^Q$ 中，因为与当前生成的 token 相关的 RoPE 矩阵将位于 $W^Q$ 和 $W^{UK}$ 之间，而矩阵乘法不遵循交换律。因此，我们必须在推理过程中重新计算所有前缀 token 的key，这将严重影响推理效率。
　　作为解决方案，我们提出了解耦 RoPE 策略，该策略使用额外的多头query ${\text{q}}_{t,i}^R\in {\mathbb{R}}^{d_h^R}$ 和共享key $k_t^R\in {\mathbb{R}}^{d_h^R}$ 来引入 RoPE，其中 $d_h^R$ 表示解耦query和key的每个头维度。配备解耦 RoPE 策略后，MLA 可执行以下计算：
$$[{\text{q}}_{t,1}^R;{\text{q}}_{t,2}^R;,...;{\text{q}}_{t,n_h}^R]={\text{q}}_t^R=RoPE(W^{QR}{\text{c}}_t^Q),\text{\hspace{1em}(14)}$$
$${\text{k}}_t^R=RoPE(W^{KR}{\text{h}}_t),\text{\hspace{1em}(15)}$$
$${\text{q}}_{t,i}=[{\text{q}}_{t,i}^C;{\text{q}}_{t,i}^R],\text{\hspace{1em}(16)}$$
$${\text{k}}_{t,i}=[{\text{k}}_{t,i}^C;{\text{k}}_t^R],\text{\hspace{1em}(17)}$$
$${\text{o}}_{t,i}=\sum _{j=1}^{t}Softma{x}_j(\frac{{\text{q}}_{t,i}^T{\text{k}}_{j,i}}{\sqrt{d_h+d_h^R}}){\text{v}}_{j,i}^C,\text{\hspace{1em}(18)}$$
$${\text{u}}_t=W^O[{\text{o}}_{t,1};{\text{o}}_{t,2};...;{\text{o}}_{t,n_h}],\text{\hspace{1em}(19)}$$
其中 $W^{QR}\in {\mathbb{R}}^{d_h^R{n}_h\times d_c^{\prime }}$ 和 $W^{KR}\in {\mathbb{R}}^{d_h^R\times d}$ 分别是用于生成解耦query和key的矩阵；RoPE(·) 表示应用 RoPE 矩阵的运算；[·; ·] 表示向量拼接运算。在推理过程中，解耦的key也应该被缓存。因此，DeepSeek-V2 需要包含 $(d_c+d_h^R)l$ 元素的总 KV 缓存。
　　为了展示MLA的完整计算过程，我们还在附录C中整理并提供了其完整公式。

2.1.4 Comparison of Key-Value Cache

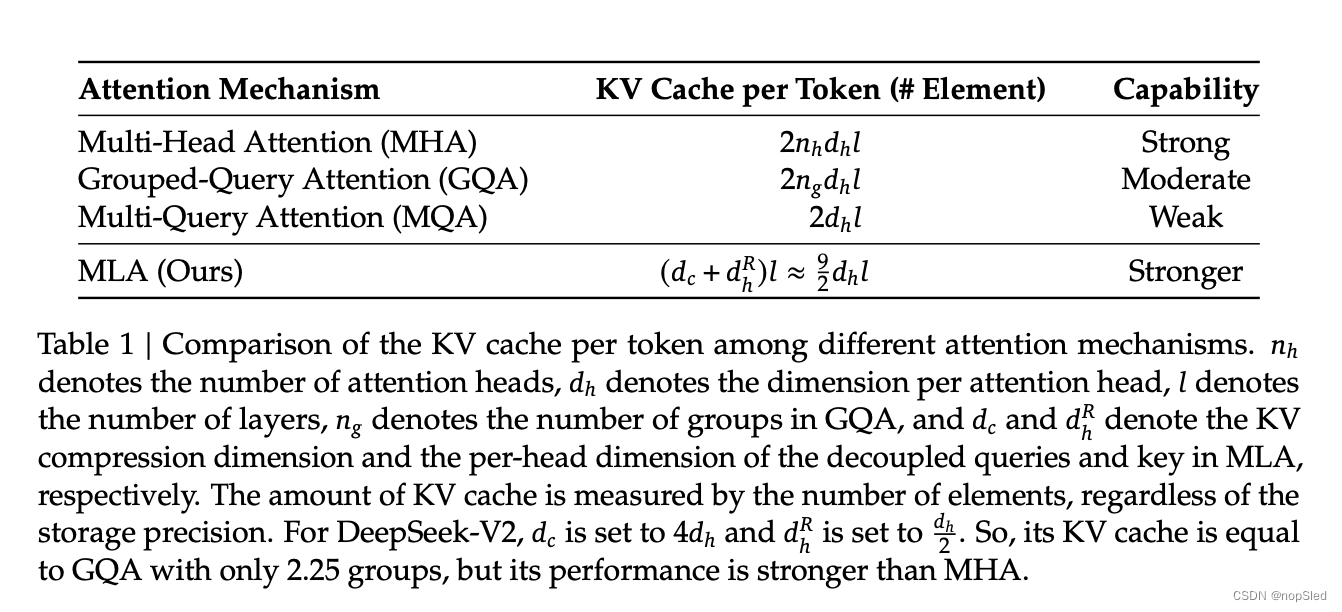
　　我们在表 1 中展示了不同注意力机制中每个 token 的 KV 缓存的比较。MLA 只需要少量的 KV 缓存，相当于只有 2.25 个组的 GQA，但可以获得比 MHA 更强的性能。

2.2 DeepSeekMoE: Training Strong Models at Economical Costs

2.2.1 Basic Architecture

对于 FFN，我们采用 DeepSeekMoE 架构。DeepSeekMoE 有两个关键思想：将专家细分为更细的粒度，以提高专家的专业化程度和更准确的知识获取；隔离一些共享专家，以减轻路由专家之间的知识冗余。在激活和总专家参数数量相同的情况下，DeepSeekMoE 的表现可以大大优于 GShard 等传统 MoE 架构。
　　令 ${\text{u}}_t$ 为第 $t$ 个 token 的 FFN 输入，我们计算 FFN 输出 $h_t^{\prime }$ 如下：
$${\text{h}}_t^{\prime }={\text{u}}_t+\sum _{i=1}^{N_s}FF{N}_i^{(s)}({\text{u}}_t)+\sum _{i=1}^{N_r}{g}_{i,t}FF{N}_i^{(r)}({\text{u}}_t),\text{\hspace{1em}(20)}$$
g i , t = { s i , t , s i , t ∈ T o p K ( { s j , t ∣ 1 ⩽ j ⩽ N r } , K r ) , 0 , o t h e r w i s e , (21) g_{i,t}= $$\begin{cases} s_{i,t}, & s_{i,t}\in TopK(\{s_{j,t}|1⩽j⩽N_r\},K_r),\\ 0, & otherwise, \end{cases}$$ \tag{21} gi,t​={si,t​,0,​si,t​∈TopK({sj,t​∣1⩽j⩽Nr​},Kr​),otherwise,​(21)
$$s_{i,t}=Softma{x}_i({\text{u}}_t^T{\text{e}}_i),\text{\hspace{1em}(22)}$$
其中