【高阶数据结构】B-数、B+树、B*树的原理

B树的概念及其特点

B树是一颗多叉的平衡搜索树，广泛应用于数据库和 文件系统中，以保持数据有序并允许高效的插入、删除和查找操作。下面介绍B树的特点：

• 多路平衡树：多路平衡树其实就是多叉平衡树，每个节点都有多个指向孩子节点的指针以及键值。通常，一颗m阶的B树有k个子节点，有k-1个关键字，而k的取值范围为[ceil(m/2),m]（celi表示向上取整）。例如一颗3阶的B树，最多有3个孩子2个关键字。
• 键值有序：每个节点中包含多个关键字，这些关键字是有序的。节点中每个关键字都将子节点切割成两部分，左边部分的节点的所有关键字的值一定是小于该关键字的，右边节点的所有关键字的值都是大于该关键字的，这一点跟二叉搜索树的性质相同。
• 树的高度平衡：所有叶子节点的深度都是一样的，站在AVL树的角度讲，每个节点的平衡因子都是0。具体如何维护这个平衡性下面会详细介绍。
• 高效的磁盘读写：B树被设计用于在磁盘上高效的存储和读取数据。通过每个节点都有多个键值和多个字节的指针，从而减少磁盘的读写次数。

下面给出一个3阶B树的节点示意图：

在设计B树节点时，孩子数量通常要多一个，这是为了方便后续实现插入操作和删除操作。概念上我们依旧认为m阶B树的节点的孩子个数为k个，实现的时候认为是k+1个。
我们将一个节点的所有键值集合称为数据域

解析B树的基本操作

插入数据

为了保证插入节点之后B树保持其平衡性，我们采用分裂节点来保持树的结构。具体的插入步骤如下：

1. 查找插入位置：首先从根节点开始，找到应该插入新键值的叶子节点。（B树每一次插入新键值都一定在叶子节点处）
2. 插入键值：在找到的叶子节点处插入新键值。如果该叶子节点的键值已经满了，即关键字的个数等于m+1，则需要对该叶子节点进行分裂。分裂的操作步骤如下：
   • 找到节点数据域的中间位置
   • 给一个新节点，将中间位置右边的所有数据（包括键值和孩子指针）搬到新节点中。新节点是被分裂节点的兄弟节点。
   • 将中间位置的键值移动放到父亲节点中，如果没有父节点，那就再创建一个父节点，并连接。

插入数据模拟

现在假设我们有一颗阶数为3的B树（每个节点最多有3个孩子和2个键值），并按以下顺序插入键值：10, 20, 5, 6, 12, 30, 7, 17。

• 当插入了10、20之后：
  
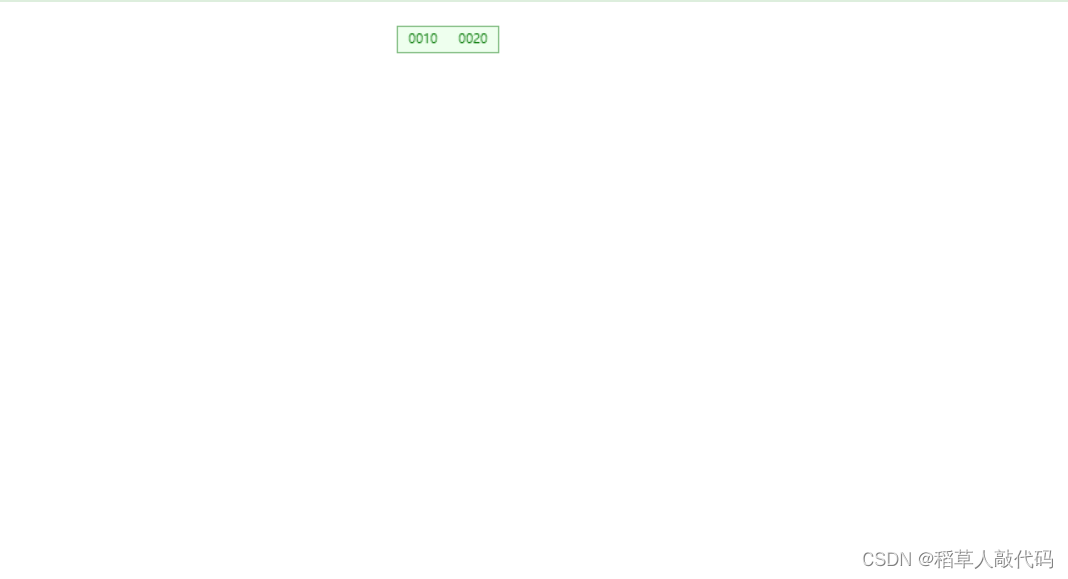
  只有一个节点，该节点已经有两个键值分别是10、20，现在这个节点的键值已经满了。
• 插入5，节点键值溢出需要分裂：
  
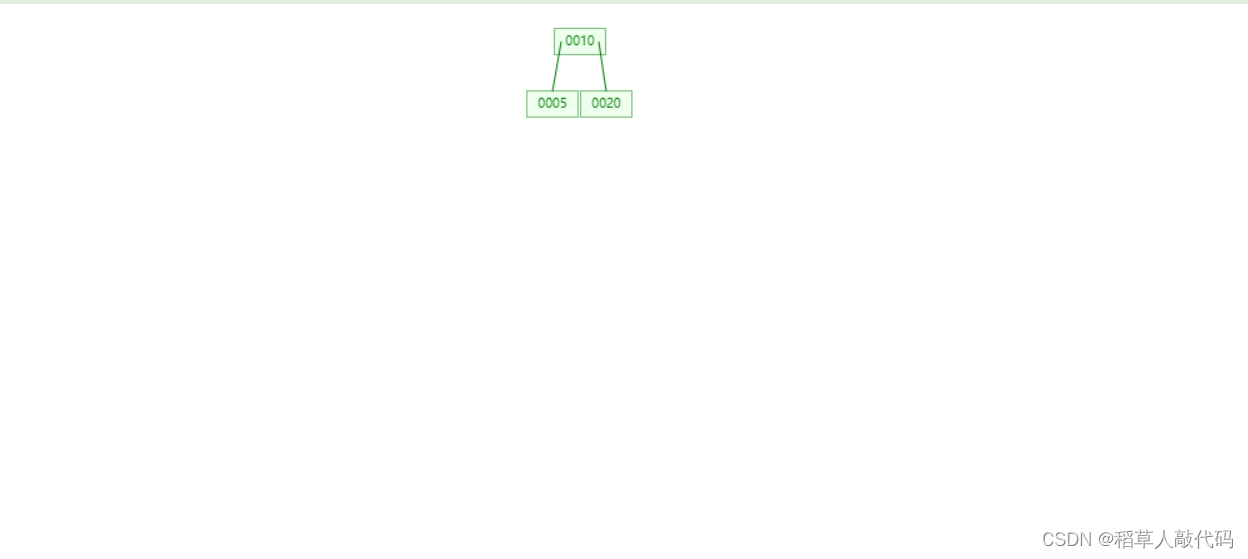
  仔细观察上述结果，根据插入数据的步骤，插入节点的键值满了，需要分裂。找到数据域的中间位置，也就是10的位置，10右边的数据全部移动到新兄弟节点中，再把中间键值10提取出来插入到父亲节点中。由于没有父节点，则新创建一个父节点。

点击观看分裂演示过程
点击观看整个插入过程

分析分裂如何维护平衡性

为什么分裂操作会保证B-树维持特性呢？以下是具体分析：

• 保证叶子节点在同一深度：分裂只是在满节点的基础上进行的，将中间键提升到父节点并不会改变叶子节点的深度差，如果父节点满了，那父节点再分裂。如果父节点不存在，那么就会创建一个新父节点，此时这个新父节点一定成为了B树的根节点，也就意味着每条叶子节点分支的高度都会+1。
• 控制节点的键值数量：每次分裂出去的键值数量都是大约一半，新的兄弟节点拥有的键值数量和被分裂节点的键值数量几乎一致。这样就保证了B树每个节点的键值数目在[ceil(m/2)−1,m−1]之间。
• 分裂后有序：由于中间键值的选择，新的兄弟节点的所有键值一定都大于被分裂节点剩下的键值。再将中间键值插入到父节点中，中间键的左孩子指向被分裂节点，右孩子指向新兄弟节点，这样一来，整颗树还是一颗搜索树。

分析B树的性能

设n为B树的总键值数量，m为B树的阶数。则每个节点最多有m个孩子节点，m-1个关键字。

• 查找效率：查找操作在B树中的时间复杂度为O(log n)，原因如下：

  • B树的高度h和节点的最小度数t以及总键值数n的关系为：h=logt(n),因为每个节点至少有t个子节点。
  • 在每个节点中查找特定键值的时间复杂度为O(t),但由于t是一个常数，所以总时间复杂度就是O(1)。（t是B树的最小度数ceil(m/2),是确定的）
  • 查找的总时间效率就是树的高度乘每个节点查找特定键值的时间，也就是O(log n)

• 插入操作：插入操作的时间复杂度也是O(log n)，具体分析如下

  • 查找到插入位置的时间复杂度为O(logn)
  • 插入后可能需要分裂节点，分裂操作的时间复杂度为O(t),这是因为每个节点最多包含t个键值。
  • 由于树的高度较小且分裂操作是局部的，整体插入操作的时间复杂度仍为O(log n)。

• 删除操作：删除操作的时间复杂度也是O(log n),具体分析：

  • 查找到目标节点的时间复杂度为O(log n)
  • 删除操作可能涉及节点的合并或键值的重新分配，这些操作的时间复杂度都是O(t),同样由于t是常数，总体的时间复杂度还是O(log n)

综上，B树各种操作时间效率都是logn。下面分析B树的空间复杂度：
B树的空间复杂度主要受到节点数目的影响。每个节点包含k-1个键值和k+1个子节点指针，节点总数与树的高度和阶数有关。由于B树是多路平衡树，其空间复杂度可以表示为O(n),其中n是键值总数。

B+树和B*树

B+树

B+树是B树的变形，在B树的基础上优化的多路平衡树，B+树的规则和B树类似，但在B树的基础上做了以下几点改进优化：

• 分支节点的子节点指针数量和关键字的个数相同（或者是子节点数量比关键字个数多1）
• 分支节点不存储实际的数据，只用于引导查找路径（存储的是孩子节点的最小关键字）
• 所有的实际数据都存在叶子节点中
• 叶子节点按照键值排序，彼此之间用一个指针连接，形成一个链表

下面给出一颗B+树结构示意图：

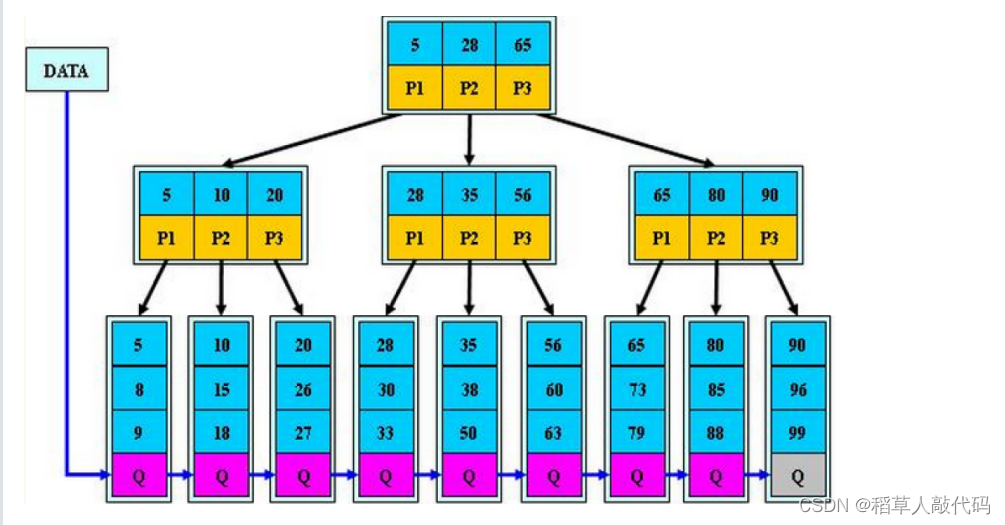
在B+树中如何查找一个数据呢？步骤如下：

和B树一致，从根节点开始逐层向下查找，比较当前键值和目标键值，如果大于目标键值，说明当前键值的孩子分支的所有值都大于目标键值。所以我们需要找到一个第一个大于目标键值的前一个键值种去寻找。点击演示B+树插入数据的动画。

B+树的分裂

当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针。

时间复杂度和空间复杂度和B数一样。

B+树的优势

• 范围查询非常高效，因为叶子节点通过链表连接，可以顺序访问所有满足范围条件的节点。范围查询性能优于B树。
• 插入和删除操作相对简单一些，因为数据只存储在叶子节点中，只需在叶子节点中维护平衡
• B+树适用于高效访问和顺序访问的场景

B*

B*树是B+树的变形，在B+树的非根和非叶子节点再增加指向兄弟节点的指针。具体结构如下：

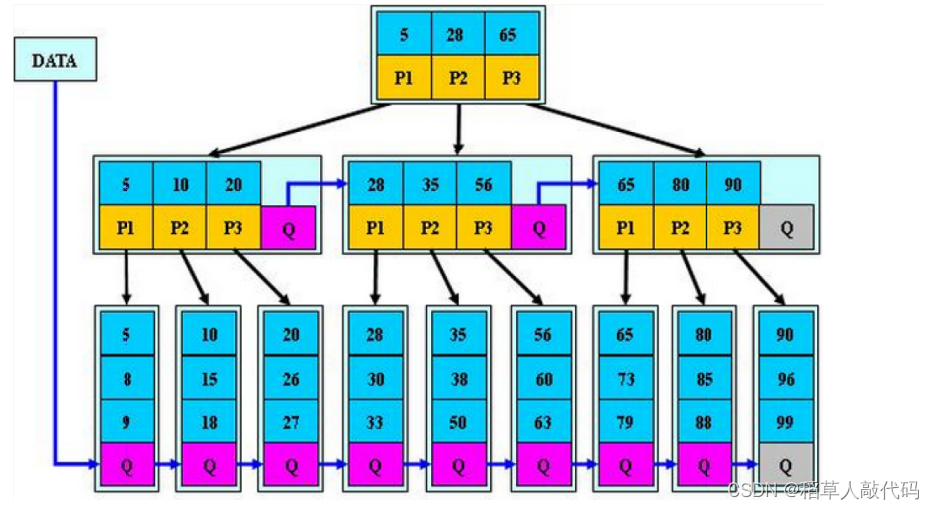
B*树的分裂

当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针。所以，B*树分配新结点的概率比B+树要低，空间使用率更高；

总结

• B树：有序数组+平衡多叉树
• B+树：有序数组链表+平衡多叉树
• B*树：一棵更丰满的，空间利用率更高的B+树