devbox
正经夜光杯
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

[ 数据结构进阶 - C++ ] 二叉搜索树_k模型和kv模型

作者：正经夜光杯 | 2024-08-15 11:01:56

赞

踩

k模型和kv模型

到如今，C++的基本语法已经了解过了。在之前，数据结构初阶是使用C语言实现的，我们进入进阶数据结构之后，将使用C++语言来实现。本篇文章我们将学习了解二叉搜索树-二叉树的进阶。

目录

1.二叉搜索树

1.1二叉搜索树的概念

1.2 二叉搜索树的操作

1.2.1 二叉搜索树的查找

1.2.2 二叉搜索树的插入

1.2.3 二叉树的删除

3.该节点有左右两个孩子

2.二叉搜索树的应用

2.1 K模型

2.2 KV模型

3.二叉搜索树的性能分析

附录：

1.二叉搜索树的模拟实现（K模型）

2.KV模型模拟实现 

1.二叉搜索树

1.1二叉搜索树的概念

二叉搜索数又称二叉排序树（BST，Binary Search Tree），它或者是一颗空树，或者是有以下性质的二叉树：

  • 若它的左子树不为空，则左子树上的所有节点的值都小于根节点的值。
  • 若它的右子树不为空，则右子树上的所有节点的值都大于根节点的值。
  • 它的左右子树也分别为二叉搜索树。

我们看两个实际的例子

1.这不是一颗二叉搜索树，因为红圈部分中，5作为7的右子树，并没有满足右子树大于根节点。

2.这是一颗二叉搜索树，树中任意一颗子树也构成二叉搜索树。满足左节点比根节点小，右节点比根节点大的性质

1.2 二叉搜索树的操作

二叉树的实现在文章附录（模拟实现，包含全部结构）

1.2.1 二叉搜索树的查找

a.从根节点开始比较，查找，比根节点大的往右边查找，比跟小的往左边查找

b.最多查找高度次，走到空若还没找到，这个值不存在。

1.查找的非递归方法：

  1. 	bool Find(const K& key)
  2. 	{
  3. 		Node* cur = _root;
  4. 		while (cur)
  5. 		{
  6. 			if (cur->_key < key)
  7. 			{
  8. 				cur = cur->_right;
  9. 			}
  10. 			else if (cur->_key > key)
  11. 			{
  12. 				cur = cur->_left;
  13. 			}
  14. 			else
  15. 			{
  16. 				return true;
  17. 			}
  18. 		}
  19. 		return false;
  20. 	}

2.查找的递归方法:

  1.     bool _FindR(Node* root, const K& key)
  2. 	{
  3. 		if (root == nullptr)
  4. 			return false;
  5.  
  6. 		if (root->_key < key)
  7. 		{
  8. 			return _FindR(root->_right, key);
  9. 		}
  10. 		else if (root->_key > key)
  11. 		{
  12. 			return _FindR(root->_left, key);
  13. 		}
  14. 		else
  15. 		{
  16. 			return true;
  17. 		}
  18. 	}

1.2.2 二叉搜索树的插入

二叉搜索树的插入具体过程：

a.树为空，则直接新增节点，赋值给root指针。

b.树不为空，按二叉搜索树性质查找插入位置，插入新节点。

我们以下图二叉树为例： 对这个课树插入12

我们在插入前需要考虑的事情以及处理方法:

插入成功的情况：

1.如果该树为空，则new一个节点，让其为根，插入成功。

2.如果该树不为空，则进行遍历找到自己属于的位置，new一个节点，赋值12，插入成功。

3.在找到自己的位置之后，我们还需要将改节点连在原树上面，因此需要一个parent节点，来判断这颗节点是parent的左孩子还是右孩子。

插入失败的情况：

1.由于性质所说，左子树均小于根节点，右子树均大于根节点，因此对于这种情况是不存在值相同的两个节点。因此一旦树中已经存在该节点，则插入失败。

考虑这些之后，我们便可以写出一个非递归版本的insert

  1. 	//插入
  2. 	bool Insert(const K& key)
  3. 	{
  4. 		if (_root == nullptr)
  5. 		{
  6. 			_root = new Node(key);
  7. 			return true;
  8. 		}
  9. 		Node* parent = nullptr;
  10. 		Node* cur = _root;
  11. 		while (cur)
  12. 		{
  13. 			if (cur->_key < key)
  14. 			{
  15. 				parent = cur;
  16. 				cur = cur->_right;
  17. 			}
  18. 			else if (cur->_key > key)
  19. 			{
  20. 				parent = cur;
  21. 				cur = cur->_left;
  22. 			}
  23. 			else
  24. 			{
  25. 				//说明相等
  26. 				return false;
  27. 			}
  28. 		}
  29.  
  30. 		cur = new Node(key);
  31. 		if (parent->_key < key)
  32. 		{
  33. 			parent->_right = cur;
  34. 		}
  35. 		else
  36. 		{
  37. 			parent->_left = cur;
  38. 		}
  39. 		return true;
  40. 	}

insert的递归有点难，先不写了 

1.2.3 二叉树的删除

二叉树的删除要查找元素是否在二叉搜索树中，如果不存在，则返回，否则要删除的结点可能分为下面四种情况：

a.要删除的节点无孩子节点

b.要删除的节点只有左孩子节点

c.要删除的节点只有右孩子节点

d.要删除的节点有左，右孩子节点

在这四种情况中，情况a和情况b或情况c可以算是一种情况。因为如果节点无孩子的时候，不写a情况，也会进入b情况和c情况。

因此可以分为：

a.该节点没有左孩子

b.该节点没有右孩子

c.该节点有两个孩子

我们首先看a情况的实现细节：

1.该节点没有左孩子

假如要删除这颗二叉树的10节点和4节点

我们依然是使用parent节点作为cur的父节点，cur为查询指针。当cur找到10节点后，如果左为空则为该种情况：

（1）如果该节点是根节点，则让根节点等于他的右孩子节点

（2）如果cur == parent->right （删除10的情况），则让parent->right = cur->right即可

（3）如果cur == parent->left （删除4的情况），则让parent->left = cur->right即可

（4）最后delete cur即可。

  1.  
  2. 				if (cur->_left == nullptr)
  3. 				{
  4. 					//判断跟
  5. 					if (cur == _root)
  6. 					{
  7. 						_root = cur->_right;
  8. 					}
  9. 					else
  10. 					{
  11. 						if (cur == parent->_right)
  12. 						{
  13. 							//cur 比 parent大
  14. 							parent->_right = cur->_right;
  15. 						}
  16. 						else
  17. 						{
  18. 							parent->_left = cur->_right;
  19. 						}
  20. 					}
  21. 					delete cur;
  22. 				}

 这部分代码为核心删除代码，全代码当删除情况讲完时呈现。

2.该节点没有右孩子

假设要删除节点14 ，逻辑和删除左孩子类似，只要掌握好链接关系即可

  1. 				else if (cur->_right == nullptr)
  2. 				{
  3. 					//判断跟
  4. 					if (cur == _root)
  5. 					{
  6. 						_root = cur->_left;
  7. 					}
  8. 					else
  9. 					{
  10. 						if (cur == parent->_right)
  11. 						{
  12. 							//cur 比 parent大
  13. 							parent->_right = cur->_left;
  14. 						}
  15. 						else
  16. 						{
  17. 							parent->_left = cur->_left;
  18. 						}
  19. 					}
  20. 					delete cur;
  21. 				}

3.该节点有左右两个孩子

如果删除的节点有两个孩子，则选择在他的右子树中寻找中序的第一个节点，也就是右子树的最小值进行替换，也可以选择左子树的最大值。例如这颗子树，要删除3和删除10

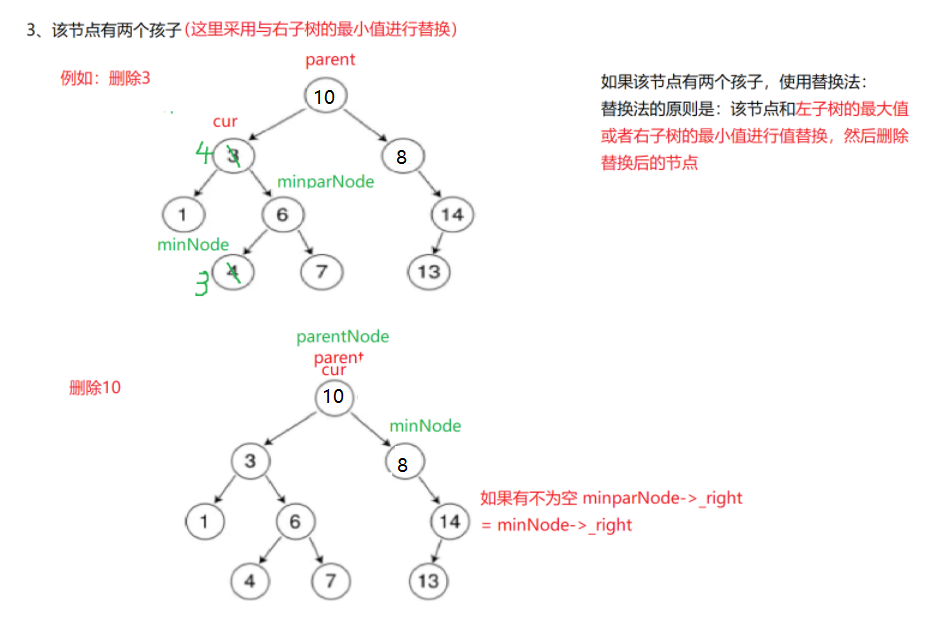
删除3：

此时需要进行节点替换，找到3节点中右子树最小的节点，然后两个节点的值进行交换，定义MinParNode = cur,MinNode，首先让MinNode指向3的右孩子，然后一直向左边找，找到节点的next为空时，则该节点就是最小的节点。此时让3和该节点进行交换。

交换完毕后，删除3就变成了删除刚刚交换的最小的节点，也就是MinNode。我们查询MinNode和MinParNode的指向关系，如果MinParNode的左孩子是MinNode，则让MinParNode的左指向MinNode的右，如果是右孩子，则让MinParNode的右指向MinNode的右。（这里为什么是MinParNode的右边指向孩子的呢？是因为MinNode已经是最小的节点了，他不可能有左孩子了，但是如果是删除10这种情况，右孩子还是有节点的，所以直接指向右解决了所有的情况）。

非递归删除代码：

  1. 	bool Erase(const K& key)
  2. 	{
  3. 		Node* parent = nullptr;
  4. 		Node* cur = _root;
  5. 		while (cur)
  6. 		{
  7. 			if (cur->_key < key)
  8. 			{
  9. 				parent = cur;
  10. 				cur = cur->_right;
  11. 			}
  12. 			else if (cur->_key > key)
  13. 			{
  14. 				parent = cur;
  15. 				cur = cur->_left;
  16. 			}
  17. 			else
  18. 			{
  19. 				//找到了
  20. 				// 1. 该节点没有左孩子
  21. 				// 2. 该节点没有右孩子
  22. 				if (cur->_left == nullptr)
  23. 				{
  24. 					//判断跟
  25. 					if (cur == _root)
  26. 					{
  27. 						_root = cur->_right;
  28. 					}
  29. 					else
  30. 					{
  31. 						if (cur == parent->_right)
  32. 						{
  33. 							//cur 比 parent大
  34. 							parent->_right = cur->_right;
  35. 						}
  36. 						else
  37. 						{
  38. 							parent->_left = cur->_right;
  39. 						}
  40. 					}
  41. 					delete cur;
  42. 				}
  43. 				else if (cur->_right == nullptr)
  44. 				{
  45. 					//判断跟
  46. 					if (cur == _root)
  47. 					{
  48. 						_root = cur->_left;
  49. 					}
  50. 					else
  51. 					{
  52. 						if (cur == parent->_right)
  53. 						{
  54. 							//cur 比 parent大
  55. 							parent->_right = cur->_left;
  56. 						}
  57. 						else
  58. 						{
  59. 							parent->_left = cur->_left;
  60. 						}
  61. 					}
  62. 					delete cur;
  63. 				}
  64. 				else
  65. 				{
  66. 					//有两个节点，替换
  67. 					Node* MinParNode = cur;
  68. 					Node* MinNode = cur->_right;
  69. 					while (MinNode->_left)
  70. 					{
  71. 						MinParNode = MinNode;
  72. 						MinNode = MinNode->_left;
  73. 					}
  74. 					swap(cur->_key, MinNode->_key);
  75. 					//if (MinNode->_right != nullptr)//自己写的  错误的
  76. 					if(MinParNode->_left == MinNode)//老师写的
  77. 					{
  78. 						MinParNode->_left = MinNode->_right;
  79. 					}
  80. 					else
  81. 					{
  82. 						MinParNode->_right = MinNode->_right;
  83. 					}
  84. 					delete MinNode;
  85. 				}
  86.  
  87. 				return true;
  88. 			}
  89. 		}
  90. 		return false;
  91. 	}

2.二叉搜索树的应用

2.1 K模型

 K模型即只有key作为关键码，结构中只需要存储key即可，关键码即为需要搜索到的值。

我们上述实现的就是K模型。

2.2 KV模型

KV模型的模拟实现在附录页

kv模型：每一个关键码key，都有预支对应的值Value，即<key，value>的键值对。这种方法也有很多使用的情况。

比如英汉词典是英文与中文的对应关系，我们可以使用KV模型，存放<word,chinese>构成键值对

3.二叉搜索树的性能分析

插入和删除操作都必须先查找，查找效率代表了二叉搜索树的各个操作的性能。

对于n个节点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是节点在二叉搜索树的深度的函数，即结点越深，则比较次数越多。

但对于同一个关键码结合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树，

最优情况下，二叉搜索树为完全二叉树(或者接近完全二叉树)，其平均比较次数为：log_2 N

最差情况下，二叉搜索树退化为单支树 ( 或者类似单支 ) ，其平均比较次数为：N
改进：如果退化成单支树，二叉搜索树的性能就失去了，因此后续我们将对二叉搜索树的插入规则进行修改，将实现出平衡二叉搜索树AVL树及其红黑树（RB树）。

附录：

1.二叉搜索树的模拟实现（K模型）

  1. //二叉搜索树结点的结构
  2. template <class K>
  3. struct BSTreeNode
  4. {
  5. 	BSTreeNode* _left;
  6. 	BSTreeNode* _right;
  7.  
  8. 	K _key;//值
  9.  
  10. 	BSTreeNode(const K& key)
  11. 		:_left(nullptr)
  12. 		,_right(nullptr)
  13. 		,_key(key)
  14. 	{}
  15.  
  16. };
  17.  
  18. //二叉树的结构
  19. template <class K>
  20. class BSTree
  21. {
  22. 	typedef BSTreeNode<K> Node;//结点重命名为Node
  23. private:
  24. 	//递归思想析构
  25. 	void DestoryTree(Node* root)
  26. 	{
  27. 		if (root == nullptr)
  28. 			return;
  29. 		DestoryTree(root->_left);
  30. 		DestoryTree(root->_right);
  31. 		delete root;
  32. 	}
  33. 	Node* CopyTree(Node* root)
  34. 	{
  35. 		if (root == nullptr)
  36. 			return nullptr;
  37. 		Node* copynode = new Node(root->_key);
  38. 		copynode->_left = CopyTree(root->_left);
  39. 		copynode->_right = CopyTree(root->_right);
  40.  
  41. 		return copynode;
  42. 	}
  43. public:
  44. 	//强制编译器自己生成构造
  45. 	//C++
  46. 	BSTree() = default;
  47.  
  48. 	BSTree(const BSTree<K>& t)
  49. 	{
  50. 		_root = CopyTree(t._root);
  51. 	}
  52.  
  53. 	//t1 = t2
  54. 	BSTree<K>& operator=(BSTree<K> t)
  55. 	{
  56. 		swap(_root, t._root);
  57. 		return *this;
  58. 	}
  59.  
  60. 	~BSTree()
  61. 	{
  62. 		DestoryTree(_root);
  63. 		_root = nullptr;
  64. 	}
  65. 	//插入
  66. 	bool Insert(const K& key)
  67. 	{
  68. 		if (_root == nullptr)
  69. 		{
  70. 			_root = new Node(key);
  71. 			return true;
  72. 		}
  73. 		Node* parent = nullptr;
  74. 		Node* cur = _root;
  75. 		while (cur)
  76. 		{
  77. 			if (cur->_key < key)
  78. 			{
  79. 				parent = cur;
  80. 				cur = cur->_right;
  81. 			}
  82. 			else if (cur->_key > key)
  83. 			{
  84. 				parent = cur;
  85. 				cur = cur->_left;
  86. 			}
  87. 			else
  88. 			{
  89. 				//说明相等
  90. 				return false;
  91. 			}
  92. 		}
  93.  
  94. 		cur = new Node(key);
  95. 		if (parent->_key < key)
  96. 		{
  97. 			parent->_right = cur;
  98. 		}
  99. 		else
  100. 		{
  101. 			parent->_left = cur;
  102. 		}
  103. 		return true;
  104. 	}
  105.  
  106. 	bool Find(const K& key)
  107. 	{
  108. 		Node* cur = _root;
  109. 		while (cur)
  110. 		{
  111. 			if (cur->_key < key)
  112. 			{
  113. 				cur = cur->_right;
  114. 			}
  115. 			else if (cur->_key > key)
  116. 			{
  117. 				cur = cur->_left;
  118. 			}
  119. 			else
  120. 			{
  121. 				return true;
  122. 			}
  123. 		}
  124. 		return false;
  125. 	}
  126. 	bool Erase(const K& key)
  127. 	{
  128. 		Node* parent = nullptr;
  129. 		Node* cur = _root;
  130. 		while (cur)
  131. 		{
  132. 			if (cur->_key < key)
  133. 			{
  134. 				parent = cur;
  135. 				cur = cur->_right;
  136. 			}
  137. 			else if (cur->_key > key)
  138. 			{
  139. 				parent = cur;
  140. 				cur = cur->_left;
  141. 			}
  142. 			else
  143. 			{
  144. 				//找到了
  145. 				// 1. 该节点没有左孩子
  146. 				// 2. 该节点没有右孩子
  147. 				if (cur->_left == nullptr)
  148. 				{
  149. 					//判断跟
  150. 					if (cur == _root)
  151. 					{
  152. 						_root = cur->_right;
  153. 					}
  154. 					else
  155. 					{
  156. 						if (cur == parent->_right)
  157. 						{
  158. 							//cur 比 parent大
  159. 							parent->_right = cur->_right;
  160. 						}
  161. 						else
  162. 						{
  163. 							parent->_left = cur->_right;
  164. 						}
  165. 					}
  166. 					delete cur;
  167. 				}
  168. 				else if (cur->_right == nullptr)
  169. 				{
  170. 					//判断跟
  171. 					if (cur == _root)
  172. 					{
  173. 						_root = cur->_left;
  174. 					}
  175. 					else
  176. 					{
  177. 						if (cur == parent->_right)
  178. 						{
  179. 							//cur 比 parent大
  180. 							parent->_right = cur->_left;
  181. 						}
  182. 						else
  183. 						{
  184. 							parent->_left = cur->_left;
  185. 						}
  186. 					}
  187. 					delete cur;
  188. 				}
  189. 				else
  190. 				{
  191. 					//有两个节点，替换
  192. 					Node* MinParNode = cur;
  193. 					Node* MinNode = cur->_right;
  194. 					while (MinNode->_left)
  195. 					{
  196. 						MinParNode = MinNode;
  197. 						MinNode = MinNode->_left;
  198. 					}
  199. 					swap(cur->_key, MinNode->_key);
  200. 					//if (MinNode->_right != nullptr)//自己写的  错误的
  201. 					if(MinParNode->_left == MinNode)//老师写的
  202. 					{
  203. 						MinParNode->_left = MinNode->_right;
  204. 					}
  205. 					else
  206. 					{
  207. 						MinParNode->_right = MinNode->_right;
  208. 					}
  209. 					delete MinNode;
  210. 				}
  211.  
  212. 				return true;
  213. 			}
  214. 		}
  215. 		return false;
  216. 	}
  217. 	//中序遍历
  218. 	void InOrder()
  219. 	{
  220. 		_InOrder(_root);
  221. 	}
  222.  
  223. 	//
  224. 	//递归方法
  225. 	bool FindR(const K& key)
  226. 	{
  227. 		return _FindR(_root, key);
  228. 	}
  229.  
  230. 	bool InsertR(const K& key)
  231. 	{
  232. 		return _InsertR(_root, key);
  233. 	}
  234.  
  235. 	bool EraseR(const K& key)
  236. 	{
  237. 		return _EraseR(_root, key);
  238. 	}
  239.  
  240. private:
  241. 	//不好理解 暂时还没理解
  242. 	bool _EraseR(Node*& root, const K& key)
  243. 	{
  244. 		if (root == nullptr)
  245. 			return false;
  246.  
  247. 		if (root->_key < key)
  248. 		{
  249. 			return _EraseR(root->_right, key);
  250. 		}
  251. 		else if (root->_key > key)
  252. 		{
  253. 			return _EraseR(root->_left, key);
  254. 		}
  255. 		else
  256. 		{
  257. 			Node* del = root;
  258. 			if (root->_left == nullptr)
  259. 			{
  260. 				root = root->_right;
  261. 			}
  262. 			else if (root->_right == nullptr)
  263. 			{
  264. 				root = root->_left;
  265. 			}
  266. 			else
  267. 			{
  268. 				Node* MinNode = root->_right;
  269. 				while (MinNode->_left)
  270. 				{
  271. 					MinNode = MinNode->_left;
  272. 				}
  273. 				swap(root->_key, MinNode->_key);
  274. 				
  275. 				return _EraseR(root->_right, key);
  276. 			}
  277. 			delete del;
  278. 			return true;
  279. 		}
  280. 	}
  281. 	bool _InsertR(Node*& root, const K& key)
  282. 	{
  283. 		if (root == nullptr)
  284. 		{
  285. 			root = new Node(key);
  286. 			return true;
  287. 		}
  288.  
  289. 		if (root->_key < key)
  290. 		{
  291. 			return _InsertR(root->_right, key);
  292. 		}
  293. 		else if (root->_key > key)
  294. 		{
  295. 			return _InsertR(root->_left, key);
  296. 		}
  297. 		else
  298. 		{
  299. 			//说明这个值已经存在了  就不再插入了
  300. 			return false;
  301. 		}
  302. 	}
  303. 	//这里之间  InsertR好理解 EraseR暂时不好理解
  304. 	bool _FindR(Node* root, const K& key)
  305. 	{
  306. 		if (root == nullptr)
  307. 			return false;
  308.  
  309. 		if (root->_key < key)
  310. 		{
  311. 			return _FindR(root->_right, key);
  312. 		}
  313. 		else if (root->_key > key)
  314. 		{
  315. 			return _FindR(root->_left, key);
  316. 		}
  317. 		else
  318. 		{
  319. 			return true;
  320. 		}
  321. 	}
  322. 	void _InOrder(Node* root)
  323. 	{
  324. 		if (root == nullptr)
  325. 			return;
  326. 		_InOrder(root->_left);
  327. 		cout << root->_key << " ";
  328. 		_InOrder(root->_right);
  329. 	}
  330.  
  331. private:
  332. 	Node* _root = nullptr;
  333. };

2.KV模型模拟实现 

  1. template<class K, class V>
  2. struct BSTreeNode
  3. {
  4. 	BSTreeNode<K, V>* _left;
  5. 	BSTreeNode<K, V>* _right;
  6.  
  7. 	const K _key;
  8. 	V _value;
  9.  
  10. 	BSTreeNode(const K& key, const V& value)
  11. 		:_left(nullptr)
  12. 		, _right(nullptr)
  13. 		, _key(key)
  14. 		, _value(value)
  15. 	{}
  16. };
  17.  
  18. template<class K, class V>
  19. class BSTree
  20. {
  21. 	typedef BSTreeNode<K, V> Node;
  22. public:
  23.  
  24. 	void InOrder()
  25. 	{
  26. 		_InOrder(_root);
  27. 		cout << endl;
  28. 	}
  29.  
  30. 	///
  31. 	Node* FindR(const K& key)
  32. 	{
  33. 		return _FindR(_root, key);
  34. 	}
  35.  
  36. 	bool InsertR(const K& key, const V& value)
  37. 	{
  38. 		return _InsertR(_root, key, value);
  39. 	}
  40.  
  41. 	bool EraseR(const K& key)
  42. 	{
  43. 		return _EraseR(_root, key);
  44. 	}
  45.  
  46. private:
  47. 	bool _EraseR(Node*& root, const K& key)
  48. 	{
  49. 		if (root == nullptr)
  50. 			return false;
  51.  
  52. 		if (root->_key < key)
  53. 		{
  54. 			return _EraseR(root->_right, key);
  55. 		}
  56. 		else if (root->_key > key)
  57. 		{
  58. 			return _EraseR(root->_left, key);
  59. 		}
  60. 		else
  61. 		{
  62. 			Node* del = root;
  63. 			// 删除
  64. 			if (root->_left == nullptr)
  65. 			{
  66. 				root = root->_right;
  67. 			}
  68. 			else if (root->_right == nullptr)
  69. 			{
  70. 				root = root->_left;
  71. 			}
  72. 			else
  73. 			{
  74. 				Node* minRight = root->_right;
  75. 				while (minRight->_left)
  76. 				{
  77. 					minRight = minRight->_left;
  78. 				}
  79.  
  80. 				swap(root->_key, minRight->_key);
  81.  
  82. 				return _EraseR(root->_right, key);
  83. 			}
  84.  
  85. 			delete del;
  86. 			return true;
  87. 		}
  88. 	}
  89.  
  90. 	bool _InsertR(Node*& root, const K& key, const V& value)
  91. 	{
  92. 		if (root == nullptr)
  93. 		{
  94. 			root = new Node(key, value);
  95. 			return true;
  96. 		}
  97.  
  98. 		if (root->_key < key)
  99. 			return _InsertR(root->_right, key, value);
  100. 		else if (root->_key > key)
  101. 			return _InsertR(root->_left, key, value);
  102. 		else
  103. 			return false;
  104. 	}
  105.  
  106. 	Node* _FindR(Node* root, const K& key)
  107. 	{
  108. 		if (root == nullptr)
  109. 			return nullptr;
  110.  
  111. 		if (root->_key < key)
  112. 		{
  113. 			return _FindR(root->_right, key);
  114. 		}
  115. 		else if (root->_key > key)
  116. 		{
  117. 			return _FindR(root->_left, key);
  118. 		}
  119. 		else
  120. 		{
  121. 			return root;
  122. 		}
  123. 	}
  124.  
  125. 	void _InOrder(Node* root)
  126. 	{
  127. 		if (root == nullptr)
  128. 			return;
  129.  
  130. 		_InOrder(root->_left);
  131. 		cout << root->_key << ":" << root->_value << endl;
  132. 		_InOrder(root->_right);
  133. 	}
  134. private:
  135. 	Node* _root = nullptr;
  136. };

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/正经夜光杯/article/detail/983259
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号