前缀和 && 差分

差分和前缀和都是算法里边比较重要的知识点，不过学习的难度并不高，这篇文章会讲解相关的内容。

1. 前缀和怎么玩

1）一维前缀和

在该数之前，包括该数的所有数之和，有点类似高中学的数列的前n项和Sn。

2）二维前缀和

根据原数组生成sum数组，sum[i][j]表示从(0, 0)到(i, j)这个范围内的累加和

求法：依次求 左 + 上 - 左上 + 自己，再从左到右，从上到下生成

*往往补第0行、第0列来减少条件判断

【图解】

Q：如果要求某个范围内的累加和怎么办？

设求(a, b)到(c, d)的累加和，则累加和就是

sum[c][d] - sum[a-1][d] - sum[c][b-1] + sum[a-1][b-1]

根据sum数组的定义和下面的图解就非常清晰了

图解如下：

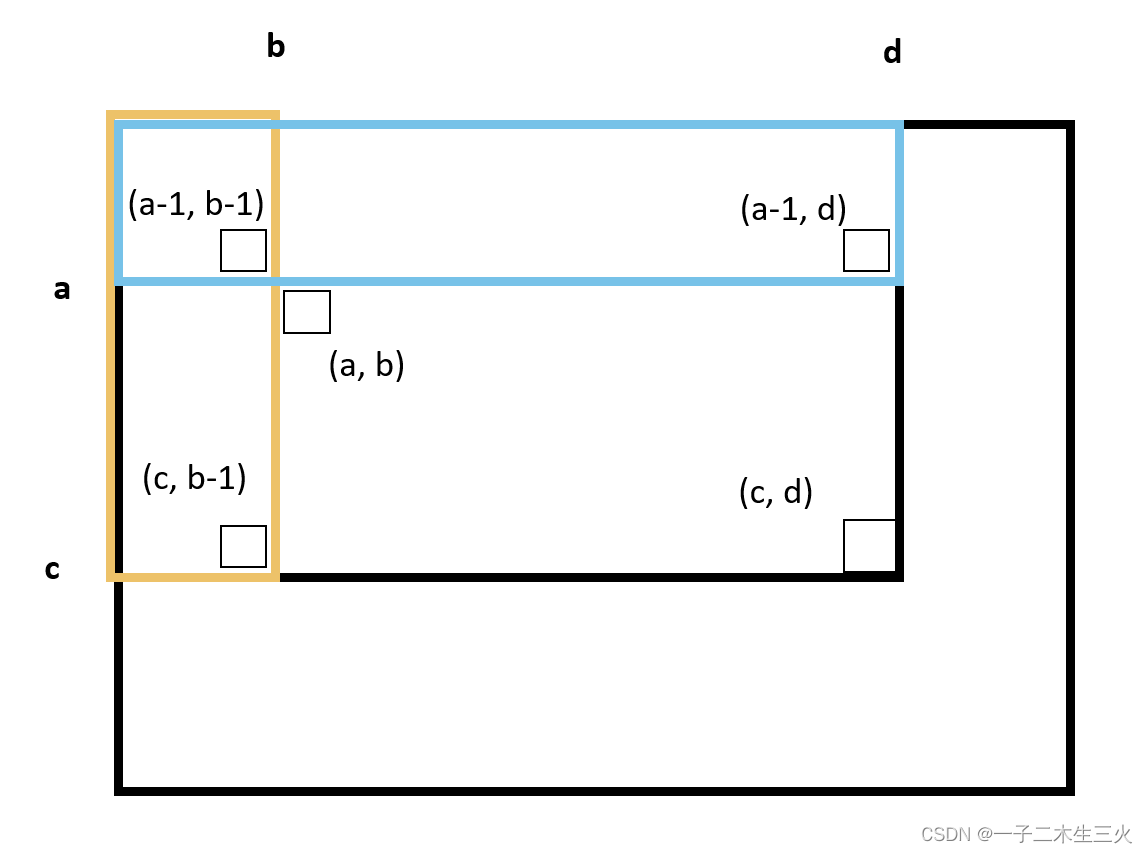
【练习】

有一道模版题，大家可以试着做做：链接

核心的思路就是二维前缀和，我的代码如下： 

class NumMatrix {
public:
    vector<vector<int>> sum;
    NumMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        sum.resize(m + 1, vector<int>(n + 1));
        
        // 第0行、第0列空出来，减少判断
        for (int a = 0, b = 1; a < m; a++, b++)
            for (int c = 0, d = 1; c < n; c++, d++)
                sum[b][d] = matrix[a][c];
        
        // 求前缀和
        for (int i = 1; i <= m; i++)
            for (int j = 1; j <= n; j++)
                sum[i][j] += sum[i - 1][j] +
                sum[i][j - 1] - sum[i - 1][j - 1];
    }
 
    int sumRegion(int row1, int col1, int row2, int col2) {
        row2++;
        col2++;
        return sum[row2][col2] - sum[row2][col1]
            - sum[row1][col2] + sum[row1][col1];
    }
};

2. 差分怎么玩

前缀和是为了下面学习差分做铺垫的，那么差分是什么玩意呢？

一般来说，差分分为3种类型，分别是一维差分、二维差分、等差差分

1）一维差分

首先，来看一个例子：

给定一个开始全为0的数组(设大小为8)，在指定下标范围进行加减操作，求多次操作后的数组

分别对2～5下标对应的数进行加3，1～3下标加2，4～6下标减2

当然，你也可以每个动作都循环一次，但是那样代码写得有点挫，而差分就是解决这样一类的问题的好方法。

【使用方式】

在每个动作的左位置下标做对应的操作，在右位置的下一个数进行逆操作，所有操作一遍后，用前缀和加工。

这是什么意思，说的是人话吗？