DWA(dynamic window approach)_动态窗口法轨迹预测

dwa介绍

DWA(动态窗口法)属于局部路径规划方法，为ROS中主要采用的方法。其原理主要是在速度空间（v,w）中采样多组速度，并模拟这些速度在一定时间内的运动轨迹，再通过一个评价函数对这些轨迹打分，最优的轨迹对应的速度被选择出来发送给机器人。

动态窗口：依据移动机器人的加减速性能限定速度采用空间在一个可行的动态范围内。

DWA的算法步骤

1.建立机器人运动模型

2.产生轨迹（利用动态窗口缩小需要搜索的动作空间）

3.评价轨迹选出最优轨迹和速度，控制机器人运动

4.代码实现

算法原理

1.机器人运动模型

在动态窗口算法中，要模拟机器人的轨迹，需要知道机器人的运动模型。它采用的是假设两轮移动机器人的轨迹是一段一段的圆弧或者直线(旋转速度为0时)，一对(Vt,Wt)就代表一个圆弧轨迹。具体推导如下：

a.非全向移动机器人（只能前进和旋转）

计算机器人的移动轨迹时，假设相邻时刻机器人的轨迹为直线，该时刻机器人自身坐标系与世界坐标系的夹角为Θ，即机器人在该时刻的位移可以简单换算成在世界坐标系的位移。

计算如下：　　　　　　　　　　

某一段时间内的轨迹累加求和：　　
　　　　　　　　　　　　　
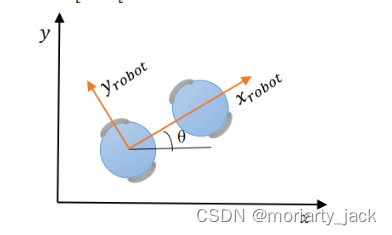
　　b.全向移动机器人（有y轴速度）

原理相同，假设相邻时刻机器人运动轨迹为直线，与世界坐标系夹角为Θ，则将该时刻内机器人的x轴为y轴方向位移依次分解到世界坐标系再累加即可。

计算如下：　　　　　　　

2.产生轨迹

动态窗口的大小受电机的线加速度、角加速度、障碍物等因素影响。

(1)计算动态窗口

a.移动机器人受自身最大速度最小速度的限制

　　b. 移动机器人受电机性能的影响:由于电机力矩有限,存在最大的加減速限制,因此移动机器人軌迹前向模拟的周期sim_period内,存在一个动态窗口,在该窗口内的速度是机器人能够实际达到的速度：　　
c.基于移动机器人安全的考虑:为了能够在碰到障碍物前停下来, 因此在最大减速度条件下, 速度有一个范围:

　(2)预测轨迹

在满足约束条件的情况下，进行速度采样（v,w），可以得到相应的轨迹：

3.评价函数（选出最优轨迹和速度）

在速度空间（v,w）中采样，根据运动学模型推测对应的轨迹，接下来引入评价函数，对轨迹进行打分，选取最优的轨迹。

一般来说，评价函数如下：

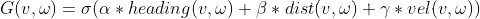
其中，

• heading(v,w)为方位角评价函数：评价机器人在当前的设定的速度下，轨迹末端朝向与目标点之间的角度差距；
• dist(v,w) 主要的意义为机器人处于预测轨迹末端点位置时与地图上最近障碍物的距离，对于靠近障碍物的采样点进行惩罚，确保机器人的避障能力，降低机器人与障碍物发生碰撞的概率；
• velocity(v,w)为当前机器人的线速度，为了促进机器人快速到达目标；δ、α、β、γ
  

4.平滑处理

代码分析

import math
import numpy as np
import matplotlib.pyplot as plt

show_animation = True  # 动画

class Config(object):
    """
    用来仿真的参数，
    """

    def __init__(self):
        # robot parameter
        self.max_speed = 1.4  # [m/s]  # 最大速度
        # self.min_speed = -0.5  # [m/s]  # 最小速度，设置为可以倒车
        self.min_speed = 0  # [m/s]  # 最小速度，设置为不倒车
        self.max_yawrate = 40.0 * math.pi / 180.0  # [rad/s]  # 最大角速度
        self.max_accel = 0.2  # [m/ss]  # 最大加速度
        self.max_dyawrate = 40.0 * math.pi / 180.0  # [rad/ss]  # 最大角加速度
        self.v_reso = 0.01  # [m/s]，速度分辨率
        self.yawrate_reso = 0.1 * math.pi / 180.0  # [rad/s]，角速度分辨率
        self.dt = 0.1  # [s]  # 采样周期
        self.predict_time = 3.0  # [s]  # 向前预估三秒
        self.to_goal_cost_gain = 1.0  # 目标代价增益
        self.speed_cost_gain = 1.0  # 速度代价增益
        self.robot_radius = 1.0  # [m]  # 机器人半径

#机器人运动方程
#在dt的时间间隔内，基于当前状态x、动作指令u=[v,w]，转移到下一个状态x，
#两个状态更新机器人的位置(x,y)，以及其超向orientation。
def motion(x, u, dt):
    """
    :param x: 位置参数，在此叫做位置空间
    :param u: 速度和加速度，在此叫做速度空间
    :param dt: 采样时间
    :return:
    """
    #假设近似，机器人在dt的时间间隔内，默认为速度与转向速度（v,w）是常数
    # 速度更新公式比较简单，在极短时间内，车辆位移也变化较大
    # 采用圆弧求解如何？
    x[0] += u[0] * math.cos(x[2]) * dt  # x方向位移
    x[1] += u[0] * math.sin(x[2]) * dt  # y方向位移
    x[2] += u[1] * dt  # 航向角
    x[3] = u[0]  # 速度v
    x[4] = u[1]  # 角速度w
    # print(x)
    return x
    
def calc_dynamic_window(x, config):
    """
    位置空间集合
    :param x:当前位置空间,符号参考硕士论文
    :param config:
    :return:目前是两个速度的交集，还差一个
    """

    # 车辆能够达到的最大最小速度
    vs = [config.min_speed, config.max_speed,
          -config.max_yawrate, config.max_yawrate]

    # 一个采样周期能够变化的最大最小速度
    vd = [x[3] - config.max_accel * config.dt,
          x[3] + config.max_accel * config.dt,
          x[4] - config.max_dyawrate * config.dt,
          x[4] + config.max_dyawrate * config.dt]
    #  print(Vs, Vd)

    # 求出两个速度集合的交集
    vr = [max(vs[0], vd[0]), min(vs[1], vd[1]),
          max(vs[2], vd[2]), min(vs[3], vd[3])]

    return vr

#产生运动轨迹
def calc_trajectory(x_init, v, w, config):
    """
    预测3秒内的轨迹
    :param x_init:位置空间
    :param v:速度
    :param w:角速度
    :param config:
    :return: 每一次采样更新的轨迹，位置空间垂直堆叠
    """
    x = np.array(x_init)
    trajectory = np.array(x)
    time = 0
    while time <= config.predict_time:
        x = motion(x, [v, w], config.dt)
        trajectory = np.vstack((trajectory, x))  # 垂直堆叠，vertical
        time += config.dt

        # print(trajectory)
    return trajectory


def calc_to_goal_cost(trajectory, goal, config):
    """
    计算轨迹到目标点的代价
    :param trajectory:轨迹搜索空间
    :param goal:
    :param config:
    :return: 轨迹到目标点欧式距离
    """
    # calc to goal cost. It is 2D norm.

    dx = goal[0] - trajectory[-1, 0]
    dy = goal[1] - trajectory[-1, 1]
    goal_dis = math.sqrt(dx ** 2 + dy ** 2)
    cost = config.to_goal_cost_gain * goal_dis

    return cost


def calc_obstacle_cost(traj, ob, config):
    """
    计算预测轨迹和障碍物的最小距离，dist(v,w)
    :param traj:
    :param ob:
    :param config:
    :return:
    """
    # calc obstacle cost inf: collision, 0:free

    min_r = float("inf")  # 距离初始化为无穷大

    for ii in range(0, len(traj[:, 1])):
        for i in range(len(ob[:, 0])):
            ox = ob[i, 0]
            oy = ob[i, 1]
            dx = traj[ii, 0] - ox
            dy = traj[ii, 1] - oy

            r = math.sqrt(dx ** 2 + dy ** 2)
            if r <= config.robot_radius:
                return float("Inf")  # collision

            if min_r >= r:
                min_r = r

    return 1.0 / min_r  # 越小越好 与障碍物距离越近，该值会越大；


def calc_final_input(x, u, vr, config, goal, ob):
    """
    计算采样空间的评价函数，选择最合适的那一个作为最终输入
    :param x:位置空间
    :param u:速度空间
    :param vr:速度空间交集
    :param config:
    :param goal:目标位置
    :param ob:障碍物
    :return:
    """
    x_init = x[:]
    min_cost = 10000.0
    min_u = u

    best_trajectory = np.array([x])

    # evaluate all trajectory with sampled input in dynamic window
    # v,生成一系列速度，w，生成一系列角速度
    for v in np.arange(vr[0], vr[1], config.v_reso): #对搜索空间dw中的v遍历
        for w in np.arange(vr[2], vr[3], config.yawrate_reso):  #对搜索空间dw中的w遍历
            # 计算出每一个可能的动作在未来一段时间内所产生的轨迹trajectory(v,w)
            trajectory = calc_trajectory(x_init, v, w, config)

            # calc cost
            to_goal_cost = calc_to_goal_cost(trajectory, goal, config)  # trajectory与目标的欧式距离
            speed_cost = config.speed_cost_gain * (config.max_speed - trajectory[-1, 3]) # v越大，该项越小，则效果越好；
            ob_cost = calc_obstacle_cost(trajectory, ob, config)   # 返回的是距离的倒数，所以该值约小，距离越大，越好
            #  print(ob_cost)

            # 评价函数多种多样，看自己选择
            # 本文构造的是越小越好
            final_cost = to_goal_cost + speed_cost + ob_cost # 总计代价，越小轨迹约好

            # search minimum trajectory
            # 在所有动态窗口划出的动作空间(v,w)里，找到一个最好的动作，在这个动作下，未来预测的轨迹评价最好
            if min_cost >= final_cost:
                min_cost = final_cost
                min_u = [v, w] #代价最小的时候的运动空间
                best_trajectory = trajectory  #记此时预测轨迹为最优轨迹

    # print(min_u)
    #  input()

    return min_u, best_trajectory


def dwa_control(x, u, config, goal, ob):
    """
    调用前面的几个函数，生成最合适的速度空间和轨迹搜索空间
    :param x: 起始位置
    :param u:初始速度空间（v,w）
    :param config:
    :param goal:目标位置
    :param ob:障碍物
    :return:
    """
    # Dynamic Window control

    vr = calc_dynamic_window(x, config) #计算动态窗口，即机器人的电机实际物理参数范围

    u, trajectory = calc_final_input(x, u, vr, config, goal, ob) #选出最优轨迹搜索空间和速度空间

    return u, trajectory


def plot_arrow(x, y, yaw, length=0.5, width=0.1):
    """
    arrow函数绘制箭头
    :param x:
    :param y:
    :param yaw:航向角
    :param length:
    :param width:参数值为浮点数，代表箭头尾部的宽度，默认值为0.001
    :return:
    length_includes_head：代表箭头整体长度是否包含箭头头部的长度，默认值为False
    head_width：代表箭头头部的宽度，默认值为3*width，即尾部宽度的3倍
    head_length：代表箭头头部的长度度，默认值为1.5*head_width，即头部宽度的1.5倍
    shape：参数值为'full'、'left'、'right'，表示箭头的形状，默认值为'full'
    overhang：代表箭头头部三角形底边与箭头尾部直接的夹角关系，通过该参数可改变箭头的形状。
    默认值为0，即头部为三角形，当该值小于0时，头部为菱形，当值大于0时，头部为鱼尾状
    """
    plt.arrow(x, y, length * math.cos(yaw), length * math.sin(yaw),
              head_length=1.5 * width, head_width=width)
    plt.plot(x, y)


def main():
    """
    主函数
    :return:
    """
    # print(__file__ + " start!!")
    # 初始化位置空间
    x = np.array([0.0, 0.0, math.pi / 2.0, 0.2, 0.0])

    goal = np.array([10, 10])

    #matrix二维矩阵 障碍物
    ob = np.matrix([[-1, -1],
                    [0, 2],
                    [4.0, 2.0],
                    [5.0, 4.0],
                    [5.0, 5.0],
                    [5.0, 6.0],
                    [5.0, 9.0],
                    [8.0, 9.0],
                    [7.0, 9.0],
                    [12.0, 12.0]
                    ])
    #ob = np.matrix([[0, 2]])
    #ob = np.matrix([[2, 2]])

    u = np.array([0.2, 0.0])  #初始速度空间(v,w)
    config = Config()  #初始化物理运动参数
    trajectory = np.array(x)  #初始轨迹空间

    for i in range(1000):
        u, best_trajectory = dwa_control(x, u, config, goal, ob) #获取最优速度空间和轨迹参数
        x = motion(x, u, config.dt) #机器人运动方程 x为机器人状态空间
        print(x)
        trajectory = np.vstack((trajectory, x))  # store state history
        if show_animation:
            draw_dynamic_search(best_trajectory, x, goal, ob)

        # check goal
        if math.sqrt((x[0] - goal[0]) ** 2 + (x[1] - goal[1]) ** 2) <= config.robot_radius:
            print("Goal!!")
            break
            
    print("Done")
    draw_path(trajectory, goal, ob, x)

def draw_dynamic_search(best_trajectory, x, goal, ob):
    """
    画出动态搜索过程图
    :return:
    """
    plt.cla()  # 清除上次绘制图像
    plt.plot(best_trajectory[:, 0], best_trajectory[:, 1], "-g")
    plt.plot(x[0], x[1], "xr")
    plt.plot(0, 0, "og")
    plt.plot(goal[0], goal[1], "ro")
    plt.plot(ob[:, 0], ob[:, 1], "bs")
    plot_arrow(x[0], x[1], x[2])
    plt.axis("equal")
    plt.grid(True)
    plt.pause(0.0001)

def draw_path(trajectory, goal, ob, x):
    """
    画图函数
    :return:
    """
    plt.cla()  # 清除上次绘制图像

    plt.plot(x[0], x[1], "xr")
    plt.plot(0, 0, "og")
    plt.plot(goal[0], goal[1], "ro")
    plt.plot(ob[:, 0], ob[:, 1], "bs")
    plot_arrow(x[0], x[1], x[2])
    plt.axis("equal")
    plt.grid(True)
    plt.plot(trajectory[:, 0], trajectory[:, 1], 'r')
    plt.show()


if __name__ == '__main__':
    main()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311

不足点

1.一条轨迹的速度和角速度(v,w)是固定的，会导致横向范围逐步变大，造成最后轨迹与可通行区域存在碰撞的问题；
2.机器人以质点来考虑，未考虑实际大小以及安全范围；