- 1产品经理的能力等级划分,你属于哪一级?
- 2python读取csv文件并生成新文件-Python 读写 CSV
- 3AI绘画Stable Diffusion基础教程:模型→效果图AI工作全流程!_stable diffusion从模型到效果渲染
- 4尚硅谷谷粒商城项目笔记——六、使用navciat连接docker中的mysql容器【电脑CPU:AMD】
- 5定制自动化pytest框架+allure报告
- 6SQL Server 基本开发规范_数据库sqlserver开发规范
- 7如何看待国产大模型现状?_国内大模型现状
- 8感觉STM32太简单是一种自负吗?
- 9海康、大华等安防摄像头、NVR,如何通过GB28181协议接入liveweb国标流媒体平台?
- 10vue实现页面打印的四种方法_vue 打印
【数据挖掘】数据挖掘总结 ( 模式挖掘 | Apriori 算法 | 支持度 | 置信度 | 关联规则 ) ★★_数据挖掘 置信度
赞
踩
一、 支持度 置信度
给定 X , Y \rm X , Y X,Y 两个项集 , 并且有 X ≥ Y \rm X \geq Y X≥Y ;
支持度 : X ⇒ Y \rm X \Rightarrow Y X⇒Y 的支持度是 X , Y \rm X , Y X,Y 两个项集在数据库 D \rm D D 中 同时出现的概率 , 即 P r ( X ∪ Y ) \rm Pr(X \cup Y) Pr(X∪Y)
置信度 : X ⇒ Y \rm X \Rightarrow Y X⇒Y 的置信度度是 X \rm X X 出现的前提下 , Y \rm Y Y 项集在数据库 D \rm D D 中同时出现的概率 , 即 P r ( Y ∣ X ) = P r ( X ∪ Y ) P r ( X ) \rm Pr(Y|X) = \cfrac{Pr(X \cup Y)}{Pr(X)} Pr(Y∣X)=Pr(X)Pr(X∪Y)
一般情况下 置信度 大于 支持度 ;
支持度用于找出 频繁项集 ;
置信度用于找出 关联规则 ;
二、 频繁项集
项集 X \rm X X 的 支持度 s u p p o r t ( X ) \rm support(X) support(X) , 大于等于 指定的 最小支持度阈值 m i n s u p \rm minsup minsup ,
则称该 项集 X \rm X X 为 频繁项集 ,
又称为 频繁项目集 ;
三、 非频繁项集
项集 X \rm X X 的 支持度 s u p p o r t ( X ) \rm support(X) support(X) , 小于 指定的 最小支持度阈值 m i n s u p \rm minsup minsup ,
则称该 项集 X \rm X X 为 非频繁项集 ,
又称为 非频繁项目集 ;
四、 Apriori 算法过程
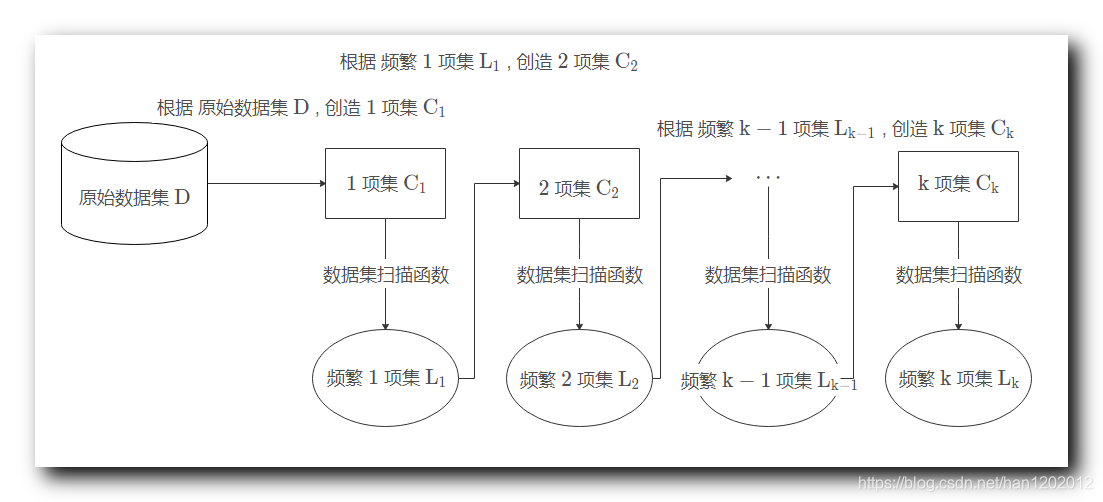
原始数据集 D \rm D D ,
1 1 1 项集 C 1 \rm C_1 C1 , 2 2 2 项集 C 2 \rm C_2 C2 , ⋯ \cdots ⋯ , k \rm k k 项集 C k \rm C_k Ck , 这些项集都是候选项集 ,
根据 原始数据集 D \rm D D , 创造 1 1 1 项集 C 1 \rm C_1 C1 , 然后对 C 1 \rm C_1 C1 执行 数据集扫描函数 , 找到其中的 频繁 1 1 1 项集 L 1 \rm L_1 L1 ,
根据 频繁 1 1 1 项集 L 1 \rm L_1 L1 , 创造 2 2 2 项集 C 2 \rm C_2 C2 , 然后对 C 2 \rm C_2 C2 执行 数据集扫描函数 , 找到其中的 频繁 2 2 2 项集 L 2 \rm L_2 L2 ,
⋮ \vdots ⋮
根据 频繁 k − 1 \rm k-1 k−1 项集 L k − 1 \rm L_{k-1} Lk−1 , 创造 k \rm k k 项集 C k \rm C_k Ck , 然后对 C k \rm C_k Ck 执行 数据集扫描函数 , 找到其中的 频繁 k \rm k k 项集 L k \rm L_k Lk ,
参考博客 : 【数据挖掘】关联规则挖掘 Apriori 算法 ( Apriori 算法过程 | Apriori 算法示例 )
五、模式挖掘示例
如下事物数据库 , 最小支持度 60 % \rm 60\% 60% , 最小置信度 80 % \rm 80\% 80% ;
| TID | Item |
|---|---|
| T1 | { M , O , N , K , E , Y } \rm \{ M, O, N , K, E, Y \} {M,O,N,K,E,Y} |
| T2 | { D , O , N , K , E , Y } \rm \{ D, O, N , K, E, Y \} {D,O,N,K,E,Y} |
| T3 | { M , A , K , E } \rm \{ M, A , K, E \} {M,A,K,E} |
| T4 | { M , U , C , K , Y } \rm \{ M, U, C , K, Y \} {M,U,C,K,Y} |
| T5 | { C , O , O , K , I , E } \rm \{ C, O, O , K, I , E \} {C,O,O,K,I,E} |
( 1 ) 使用 Apriori 算法找出所有频繁项集 ;
( 2 ) 写出关联规则 ;
( 1 ) 使用 Apriori 算法找出所有频繁项集 :
根据原始数据集 D \rm D D 创造 1 1 1 项集 C 1 \rm C_1 C1 , 如下 :
| Item | 支持度 |
|---|---|
| { A } \rm \{ A \} {A} | 20 % \rm 20\% 20% |
| { C } \rm \{ C \} {C} | 40 % \rm 40\% 40% |
| { E } \rm \{ E \} {E} | 80 % \rm 80\% 80% |
| { I } \rm \{ I \} {I} | 20 % \rm 20\% 20% |
| { K } \rm \{ K \} {K} | 80 % \rm 80\% 80% |
| { M } \rm \{ M \} {M} | 60 % \rm 60\% 60% |
| { N } \rm \{ N \} {N} | 40 % \rm 40\% 40% |
| { O } \rm \{ O \} {O} | 60 % \rm 60\% 60% |
| { U } \rm \{ U \} {U} | 20 % \rm 20\% 20% |
| { Y } \rm \{ Y \} {Y} | 60 % \rm 60\% 60% |
对 1 1 1 项集 C 1 \rm C_1 C1 执行数据集扫描函数 , 找到频繁 1 1 1 项集 L 1 \rm L_1 L1 , 即筛选出支持度大于等于 60 % \rm 60\% 60% 的 1 1 1 项集 :
| Item | 支持度 |
|---|---|
| { E } \rm \{ E \} {E} | 80 % \rm 80\% 80% |
| { K } \rm \{ K \} {K} | 80 % \rm 80\% 80% |
| { M } \rm \{ M \} {M} | 60 % \rm 60\% 60% |
| { O } \rm \{ O \} {O} | 60 % \rm 60\% 60% |
| { Y } \rm \{ Y \} {Y} | 60 % \rm 60\% 60% |
根据 频繁 1 1 1 项集 L 1 \rm L_1 L1 创造 2 2 2 项集 C 2 \rm C_2 C2 , 如下 :
| Item | 支持度 |
|---|---|
| { E , K } \rm \{ E , K \} {E,K} | 80 % \rm 80\% 80% |
| { E , M } \rm \{ E, M \} {E,M} | 40 % \rm 40\% 40% |
| { E , O } \rm \{ E,O \} {E,O} | 60 % \rm 60\% 60% |
| { E , Y } \rm \{ E,Y \} {E,Y} | 40 % \rm 40\% 40% |
| { K , M } \rm \{ K,M \} {K,M} | 40 % \rm 40\% 40% |
| { K , O } \rm \{ K,O \} {K,O} | 60 % \rm 60\% 60% |
| { K , Y } \rm \{ K,Y \} {K,Y} | 60 % \rm 60\% 60% |
| { M , O } \rm \{ M,O \} {M,O} | 20 % \rm 20\% 20% |
| { M , Y } \rm \{ M,Y \} {M,Y} | 40 % \rm 40\% 40% |
| { O , Y } \rm \{ O,Y \} {O,Y} | 40 % \rm 40\% 40% |
对 2 2 2 项集 C 2 \rm C_2 C2 执行数据集扫描函数 , 找到频繁 2 2 2 项集 L 2 \rm L_2 L2 , 即筛选出支持度大于等于 60 % \rm 60\% 60% 的 2 2 2 项集 :
| Item | 支持度 |
|---|---|
| { E , K } \rm \{ E , K \} {E,K} | 80 % \rm 80\% 80% |
| { E , O } \rm \{ E,O \} {E,O} | 60 % \rm 60\% 60% |
| { K , O } \rm \{ K,O \} {K,O} | 60 % \rm 60\% 60% |
| { K , Y } \rm \{ K,Y \} {K,Y} | 60 % \rm 60\% 60% |
根据 频繁 2 2 2 项集 L 2 \rm L_2 L2 创造 3 3 3 项集 C 3 \rm C_3 C3 , 如下 :
| Item | 支持度 |
|---|---|
| { E , K , O } \rm \{ E , K, O \} {E,K,O} | 60 % \rm 60\% 60% |
| { E , O , Y } \rm \{ E,O , Y\} {E,O,Y} | 40 % \rm 40\% 40% |
| { K , O , Y } \rm \{ K,O , Y\} {K,O,Y} | 40 % \rm 40\% 40% |
对 3 3 3 项集 C 3 \rm C_3 C3 执行数据集扫描函数 , 找到频繁 3 3 3 项集 L 3 \rm L_3 L3 , 即筛选出支持度大于等于 60 % \rm 60\% 60% 的 3 3 3 项集 :
| Item | 支持度 |
|---|---|
| { E , K , O } \rm \{ E , K, O \} {E,K,O} | 60 % \rm 60\% 60% |
最终得出结果 :
频繁 1 1 1 项集 : { E } , { K } , { M } , { O } , { Y } , \rm \{E\},\{K\},\{M\},\{O\},\{Y\}, {E},{K},{M},{O},{Y},
频繁 2 2 2 项集 : { E , K } , { E , O } , { K , O } , { K , Y } \rm \{E,K\},\{E,O\},\{K,O\},\{K,Y\} {E,K},{E,O},{K,O},{K,Y}
频繁 3 3 3 项集 : { E , K , O } \rm \{E,K,O\} {E,K,O}
( 2 ) 写出关联规则 ;
置信度大于等于 80 % \rm 80\% 80% 就说明有关联规则 ;
基于 频繁 2 2 2 项集 L 2 \rm L_2 L2 的关联规则 :
| 置信度 | |
|---|---|
| E ⇒ K \rm E \Rightarrow K E⇒K | E K E = 4 4 = 1 \rm \cfrac{EK}{E} = \cfrac{4}{4} = 1 EEK=44=1 |
| K ⇒ E \rm K \Rightarrow E K⇒E | E K K = 4 5 = 0.8 \rm \cfrac{EK}{K} = \cfrac{4}{5} = 0.8 KEK=54=0.8 |
| E ⇒ O \rm E \Rightarrow O E⇒O | E O E = 3 4 = 0.75 \rm \cfrac{EO}{E} = \cfrac{3}{4} = 0.75 EEO=43=0.75 |
| O ⇒ E \rm O\Rightarrow E O⇒E | E O O = 3 3 = 1 \rm \cfrac{EO}{O} = \cfrac{3}{3} = 1 OEO=33=1 |
| K ⇒ O \rm K \Rightarrow O K⇒O | K O K = 3 5 = 0.6 \rm \cfrac{KO}{K} = \cfrac{3}{5} = 0.6 KKO=53=0.6 |
| O ⇒ K \rm O \Rightarrow K O⇒K | K O O = 3 3 = 1 \rm \cfrac{KO}{O} = \cfrac{3}{3} = 1 OKO=33=1 |
| K ⇒ Y \rm K \Rightarrow Y K⇒Y | E K E = 3 5 = 0.6 \rm \cfrac{EK}{E} = \cfrac{3}{5} = 0.6 EEK=53=0.6 |
| Y ⇒ K \rm Y \Rightarrow K Y⇒K | E K E = 3 3 = 1 \rm \cfrac{EK}{E} = \cfrac{3}{3} = 1 EEK=33=1 |
基于 频繁 3 3 3 项集 L 3 \rm L_3 L3 的关联规则 :
| 置信度 | |
|---|---|
| E ⇒ K , O \rm E \Rightarrow K,O E⇒K,O | E K O E = 3 4 = 0.75 \rm \cfrac{EKO}{E} = \cfrac{3}{4} = 0.75 EEKO=43=0.75 |
| K , O ⇒ E \rm K,O \Rightarrow E K,O⇒E | E K O K O = 3 3 = 1 \rm \cfrac{EKO}{KO} = \cfrac{3}{3} = 1 KOEKO=33=1 |
| K ⇒ E , O \rm K \Rightarrow E,O K⇒E,O | K E O K = 3 5 = 0.6 \rm \cfrac{KEO}{K} = \cfrac{3}{5} = 0.6 KKEO=53=0.6 |
| E , O ⇒ K \rm E,O\Rightarrow K E,O⇒K | E O K E O = 3 3 = 1 \rm \cfrac{EOK}{EO} = \cfrac{3}{3} = 1 EOEOK=33=1 |
| O ⇒ E , K \rm O \Rightarrow E,K O⇒E,K | O E K O = 3 4 = 0.75 \rm \cfrac{OEK}{O} = \cfrac{3}{4} = 0.75 OOEK=43=0.75 |
| E , K ⇒ O \rm E,K \Rightarrow O E,K⇒O | E K O E K = 3 4 = 0.75 \rm \cfrac{EKO}{EK} = \cfrac{3}{4} = 0.75 EKEKO=43=0.75 |
根据置信度 ≥ 80 % \rm \geq 80\% ≥80%关联规则有 :
L 2 \rm L_2 L2 关联规则 : E ⇒ K \rm E \Rightarrow K E⇒K , K ⇒ E \rm K \Rightarrow E K⇒E , O ⇒ E \rm O\Rightarrow E O⇒E , O ⇒ K \rm O \Rightarrow K O⇒K , Y ⇒ K \rm Y \Rightarrow K Y⇒K ;
L 3 \rm L_3 L3 关联规则 : K , O ⇒ E \rm K,O \Rightarrow E K,O⇒E , E , O ⇒ K \rm E,O\Rightarrow K E,O⇒K ;


