【分治算法】_用c语言实现把n个元素的集合划分成m个元素的子集合,求出子集合的个数

分治算法

A

Problem A. 集合划分

时间限制 1000 ms
内存限制 64 MB

题目描述

n个元素的集合{1,2,…, n }可以划分为若干个非空子集。例如，当n=4 时，集合{1，2，3，4}可以划分为15 个不同的非空子集如下：
略，md会报错
给定正整数n，计算出n 个元素的集合{1,2,…, n }可以划分为多少个不同的非空子集。

输入数据

多组输入(<=10组数据，读入以EOF结尾) 每组一行输入一个数字，n(0<n<=18)

输出数据

每组输出一行结果。

样例输入

4
1

样例输出

15
1

#include <iostream>
using namespace std;
int n;
long long int count = 0;
//设n个元素的集合可以划分为F(n, m) 个不同的由m个非空子集组成的集合。
long long int getAllSubset(int n, int m)
{
    if (m == 1 || n == m)
        return 1;
    else
        return getAllSubset(n - 1, m - 1) + getAllSubset(n - 1, m) * m;
}
int main()
{
    while (scanf("%d", &n) != EOF)
    {
        count = 0;
        for (int i = 1; i <= n; i++)
        {
            count += getAllSubset(n, i);
        }
        cout << count << endl;
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

B

Problem B. 二叉树的后序遍历

时间限制 1000 ms
内存限制 64 MB

题目描述

给你一个二叉树，按照后序遍历的顺序输出这棵树。

输入数据

第一行一个整数 n (1≤n≤1e4) ，表示这棵树的节点数。 接下来有 n-1 行，每行有两个整数 u,v ，表示节点 u 到节点 v 有一条边，输入保证树以 1 为根，且 u 为 v 的父节点。对于一个节点的多个子节点，将更早输入的那一个子节点的视为他的左子节点。

输出数据

输出该树的后序遍历，节点编号之间用一个空格分隔。

样例输入

6
1 2
2 3
3 4
1 5
5 6
1
2
3
4
5
6

样例输出

4 3 2 6 5 1
1

样例说明

后序遍历的定义是：对访问的每个树，先访问他的左子树，然后访问他的右子树，最后访问根节点。

#include <stdio.h>
#include<stdlib.h>
#define MaxSize 10010
int n, a[MaxSize][2];;
void post_order(int x)
{
	bool isdata = true;
	for (int i = 0; i < n - 1; i++)
	{
		if (a[i][0] == x)
		{
			post_order(a[i][1]);
			for (i++; i < n - 1; i++)
			{
				if (a[i][0] == x)post_order(a[i][1]);
			}
		}//6 1 2 2 3 3 4 1 5 5 6

	}
	printf("%d ", x);
	return;
}
int main()
{
	scanf("%d", &n);
	for (int i = 0; i < n - 1; i++)
	{
		scanf("%d", &a[i][0]);
		scanf("%d", &a[i][1]);
	}
	post_order(1);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

C

Problem C. 整数的幂次方表示

时间限制 1000 ms
内存限制 64 MB

题目描述

输入数据

一行一个正整数n(1<=n<=20000)

输出数据

符合约定的 n 的 0,2表示（在表示中不能有空格）。

样例输入

1315
1

样例输出

2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)
1

#include<stdio.h>

void cal(int m, int n)
//m为被分解的数，n为二进制位数，r为位数上的数值。
{
	int r;
	if (m == 0)//m 已经被分解完，返回
		return;
	r = m % 2;
	m = m / 2;
	cal(m, n + 1);
	if (m != 0 && r != 0)
		//如果m不为0且r不为0证明这不是第一个2的幂次方，输出+
	{
		printf("+");
	}
	if (r == 1)
	{
		if (n == 0)
			printf("2(0)");
		else if (n == 1)
			printf("2");
		else if (n == 2)
			printf("2(2)");
		else
		{
			printf("2(");
			cal(n, 0);
			//如果指数不能用2(0),2,2(2)表示则继续分解
			printf(")");
		}
	}
}
int main()
{
	int num;
	scanf("%d", &num);
	cal(num, 0);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

D

Problem D. 最近点对

时间限制 1000 ms
内存限制 64 MB

题目描述

有n个坐标点，问这些点之间最近的一对点的距离是多少？

输入数据

多组输入(<=10组数据，读入以EOF结尾)。 每组第一行输入一个数字，n(1<=n<=100000) 表示坐标点的个数。 随后n行，为两个整数，表示对应的坐标点。

输出数据

每组输出一行结果，保留两位有效数字

样例输入

2
0 0
1 1
1
2
3

样例输出

1.41
1

E

Problem E. 小明的散步路径

时间限制 1000 ms
内存限制 64 MB

题目描述

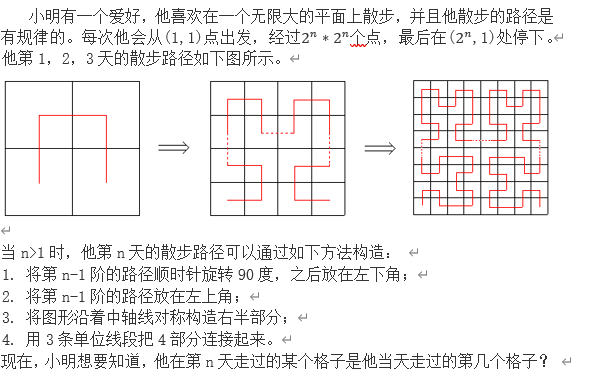
输入数据

一行三个整数n,x,y(1<=n<=14,1<=x,y<=2n2n) 。

输出数据

一行一个整数k，表示坐标为(x,y)的格子是他第n天走过的第k个格子。

样例输入

1 1 2
1

样例输出

2
1

#define _CRT_SECURE_NO_WARNINGS
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
int fun(int n, int x, int y)
{
	if (n == 1) {
		if (x == y && y == 1) return 1;
		if (x == 1 && y == 2) return 2;
		if (x == y && y == 2) return 3;
		if (x == 2 && y == 1) return 4;
	}
	if (n != 1) {
		int res = 0, mid = pow(2, n - 1);
		if (x <= mid && y <= mid) {
			res = fun(n - 1, y, x);
		}
		else if (x <= mid && y > mid) {
			res = mid * mid + fun(n - 1, x, y - mid);
		}
		else if (x > mid && y > mid) {
			res = 2 * mid * mid + fun(n - 1, x - mid, y - mid);
		}
		else {
			res = 3 * mid * mid + fun(n - 1, mid - y + 1, pow(2, n) - x + 1);
		}
		return res;
	}
}

int main()
{
	int n, x, y;
	while (scanf("%d%d%d", &n, &x, &y) != EOF) {
		cout << fun(n, x, y) << endl;
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

##　Ｆ

Problem F. 气球游戏

时间限制 10000 ms
内存限制 64 MB

题目描述

刚刚今天去游乐场玩，发现了一个新的游戏项目，游戏是这样的，场上一共有 n 个气球，它们的编号是0到n-1，然后每个气球上还有一个数字，我们使用数组nums来保存这些数字。

现在游戏要求刚刚戳破所有的气球。每当刚刚戳破一个气球i时，刚刚可以获得nums[left] * nums[i] * nums[right]个积分。这里的left和right指的是和i相邻的两个气球的序号。（注意每当刚刚戳破了气球i后，气球left和气球right就变成了相邻的气球。）

求所能获得积分的最大值。

输入数据

输入中有若干组测试样例，第一行为一个正整数T(T≤1000)，表示测试样例组数。每组测试样例包含2部分： 第一部分有一行，包含1个正整数n（0≤n≤500），第二部分为一行，有n个数，第i个数表示num[i],(0≤num[i]≤100)。

输出数据

对每组测试数据，单独输出一行答案，表示最大的积分值

样例输入

1
4
3 1 5 8
1
2
3

样例输出

167
1

#include <stdio.h>
#include <iostream>
#include <vector>
#include <math.h>
#include <algorithm>
#include <iostream>
using namespace std;
class Solution {
public:
	int maxCoins(vector<int>& nums) {
		int n = nums.size();
		vector<vector<int>> rec(n + 2, vector<int>(n + 2));
		vector<int> val(n + 2);
		val[0] = val[n + 1] = 1;
		for (int i = 1; i <= n; i++) {
			val[i] = nums[i - 1];
		}
		for (int i = n - 1; i >= 0; i--) {
			for (int j = i + 2; j <= n + 1; j++) {
				for (int k = i + 1; k < j; k++) {
					int sum = val[i] * val[k] * val[j];
					sum += rec[i][k] + rec[k][j];
					rec[i][j] = max(rec[i][j], sum);
				}
			}
		}
		return rec[0][n + 1];
	}
}s;
int main()
{
	int T, n, tmp;
	vector<int> num;
	cin >> T;
	for (int j=0;j<T;j++)
	{
		cin >> n;
		for (int i = 0; i < n; i++) {
			cin >> tmp;
			num.push_back(tmp);
		}
		cout << s.maxCoins(num) << endl;
		num.clear();
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46