热门标签
热门文章
- 1【Proteus仿真】51单片机+DC MOTOR PWM调速实验二_单片机motor-dc里面的数字怎么改
- 2【Spring】SpringCache整合redis做缓存_springcatch 缓存
- 3RabbitMQ 参数配置说明_spring.rabbitmq.virtual-host
- 4海康工业相机Python+OpenCV调用实现取流_enum devices fail! ret[0x80000006]
- 5在Windows下安装mysql步骤_mysql8.4win安装教程
- 6解决Mac 应用已损坏打不开的问题_is damaged and can鈥檛 be opened. you should move it
- 7org.apache.zookeeper.KeeperException$ConnectionLossException报错的解决方案
- 8Windows系统电脑本地运行大语言模型Ollama结合cpolar内网穿透远程连接思源笔记智能写作_ollama 局域网访问
- 9Uipath Error loading Python script_error loading script: swapper.py
- 107月最新字节跳动Java三面面经分享(框架+线程_字节跳动三面java
当前位置: article > 正文
2.线性神经网络
作者:从前慢现在也慢 | 2024-06-14 07:11:26
赞
踩
2.线性神经网络
1.线性回归
一个简化模型
- 假设1:影响放假的关键因素是卧室个数,卫生间个数和居住面积,记为x1,x2,x3
- 假设2:成交价实关键因素的加权和 y = w1 * x1 + w2 * x2 + w3 * x3 +b
权重和偏差的实际值在后面决定
线性模型:可以看做是单层神经网络
- 给定n维输入 x = [x1,x2,…xn]
- 线性模型有一个n维权重和一个标量偏差
- w = [w1,w2,…,wn] b
- 输入是输出的加权和
- y = w1 * x1 + w2 * x2 +…+wn * xn + b
- 向量版:y = <w , x> + b
衡量预估质量
- 比较真实值和预估值,例如房屋售价和估价
- 假设y是真实值,z是估计值,我们可以比较
- L(y,z) = 1/2(y-z)^2 这个叫做平方损失
训练数据
- 收集一些数据点来决定参数值(权重和偏差),例如过去6个月卖的房子
- 这被称为训练数据
- 通常越多越好
- 假设我们有n个样本,记
- X =[x1,x2,x3…xn] y = [y1,y2,y3…yn]
参数学习
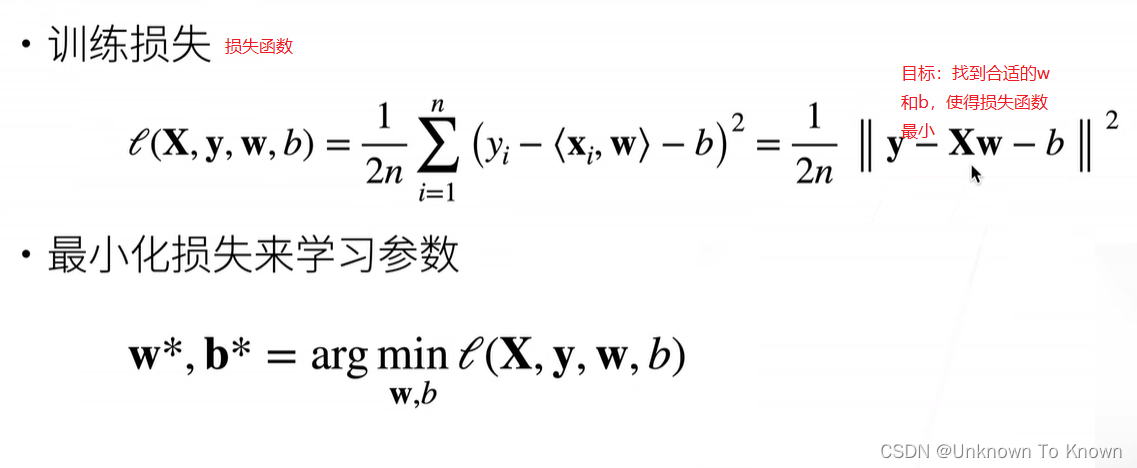
显示解

总结
- 线性回归是对N维输入的加权,外加偏差
- 使用平方损失来衡量预测值和真实值的差异
- 线性回归有显示解,一般都网络都是非线性的没有显示解
- 线性回归可以看做是单层神经网络
2.基础优化方法
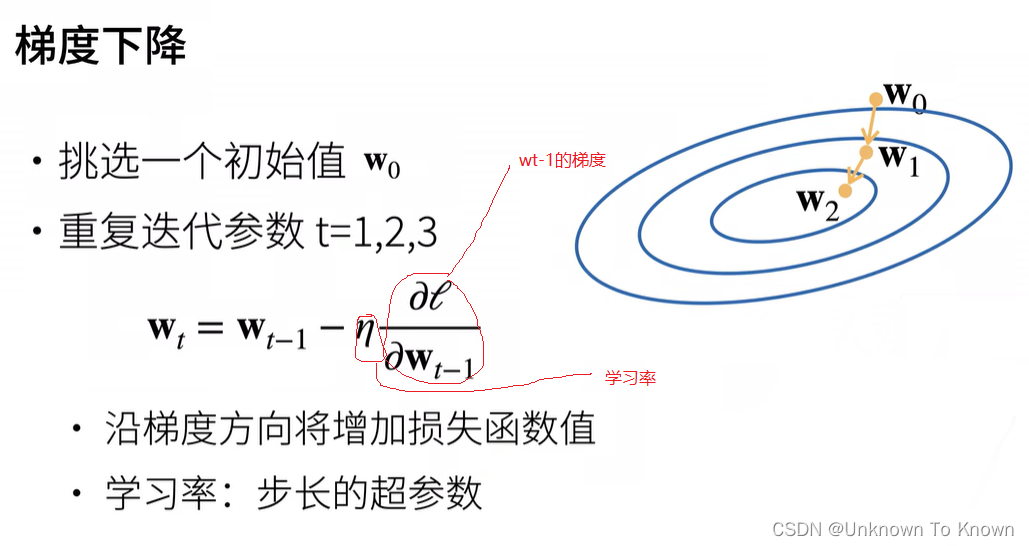
梯度:使得损失函数增加最快的方向
负梯度:是损失函数减小最快的方向
小批量随机梯度下降
在实际中我们很少使用梯度下降,深度学习中最常用的小批量随机梯度下降
- 在整个训练集上算梯度太贵
- 一个深度神经网络模型可能需要数分钟至数小时

- 一个深度神经网络模型可能需要数分钟至数小时
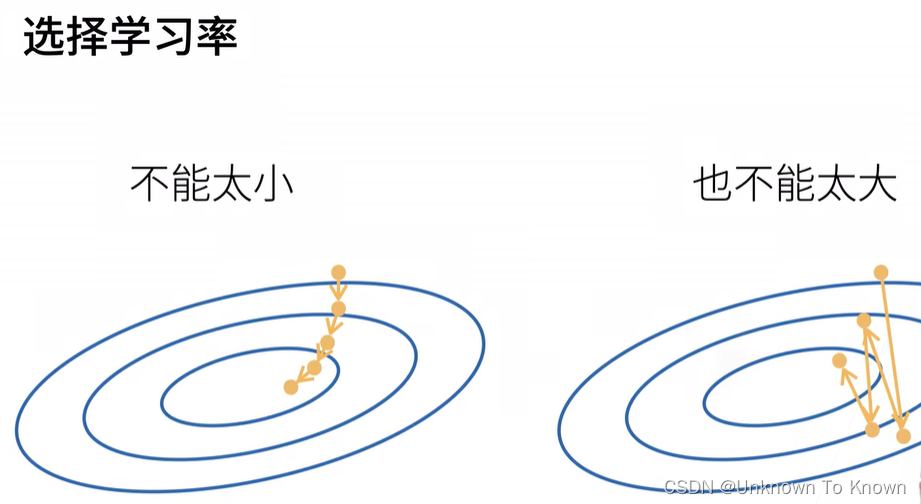
选择批量大小
- 不能太小:每次计算量太小,不适合并行来最大利用计算资源
- 不能太大:内存消耗增加浪费计算
总结
- 梯度下降通过不断沿着反梯度方向更新参数求解
- 小批量随机梯度下降是深度学习默认的求解算法
- 两个重要的超参数是批量大小和学习率
3.Softmax回归:其实是一个分类问题
回归VS分类
- 回归估计一个连续值:如房价的预测
- 分类预测一个离散类别:如猫狗等图片分类
MNIST:手写数字识别(10类)
ImageNet:自然物体分类(1000类)
Kaggle上的分类问题:Kaggle一个数据建模和数据分析竞赛平台
- 将人类蛋白质显微镜图片分成28类
- 将恶意软件分成9个类
- 将恶意的Wikopedia评论分成7类
回归
- 单连续数值输出
- 自然区间R
- 跟真实值的区别做为损失
分类
- 通常多个输出
- 输出i是预测为第i类的置信度
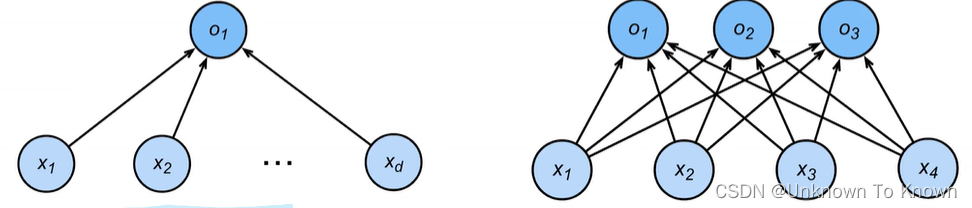
从回归到多类分类—均方损失
针对分类来讲,不关心他们之间的实际的值,是关心对正确类别的置信度特别大。
假设oy为真实值 oi为预测值,他们不关心oi的大小
他们是关系 oy - oi 大于等于 某个阀值,或者说我们正确的oi要远远大于其他类别的oi

Softmax和交叉熵损失

4.损失函数
损失函数用来衡量真实值和预测值的区别。介绍三个基本损失函数
L2 Loss(L2范式)
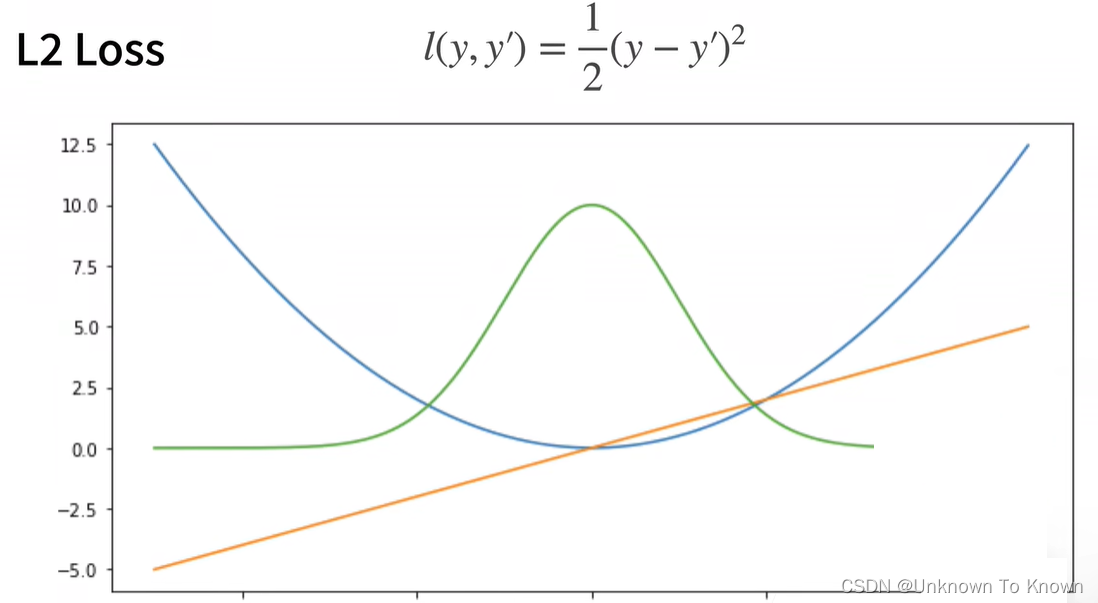
橙色线为:梯度
绿色线为:它的似然函数,高斯分布
蓝色线为:y = 0时变换y’的函数
蓝线代表真实值和预测值的差值,当它大时,梯度值也是较大的
L1 Loss

这种损失函数的特性:不管预测值和真实值相差多远,我的梯度永远是常数,所以权重更新稳定,但是此函数零点出不可导,所以它具有不平滑性,当你的预测值和真实值靠近时,会有剧烈变化
Huber Robust Loss
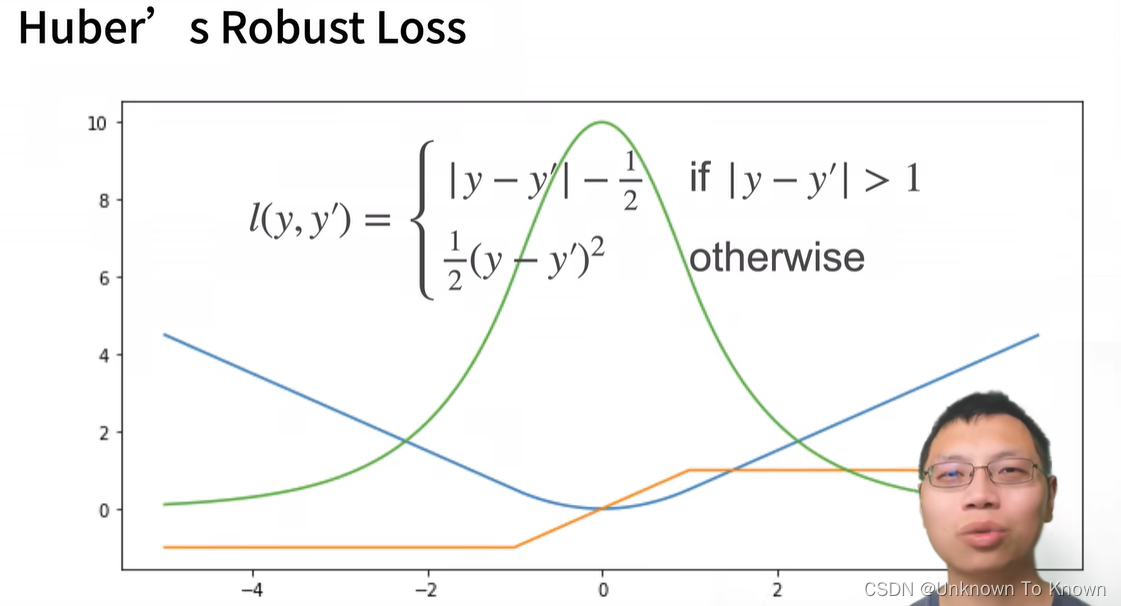
当你的y’(导数)大于1时,是L1,当y’小于1时,是L2
这个相当于L1和L2的结合,避免L1的不平滑性和L2在开始的不稳定性
5.从零开始实现Softmax回归
import torch from IPython import display from d2l import torch as d2l batch_size = 256 #load_data_fashion_mnist加载 Fashion-MNIST 数据集 10个类别的服饰图片数据集,每个类别包含7000张28x28像素的灰度图像。 #获取了两个迭代器 train_iter 和 test_iter 每次256张图像和对应的标签 train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size) #每张图片是28 * 28 * 1但是Softmax输入为向量,要把图片拉成向量 num_inputs = 784#28*28=784 num_outputs = 10#10个类 #定义权重和偏置 #w 以均值 0、标准差 0.01 的正态分布随机初始化,大小为 (num_inputs, num_outputs) 的张量 W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True) #b 是一个大小为 (num_outputs,) 的张量,其中 num_outputs 是输出的数量。通过 torch.zeros() 函数以全零初始化 b = torch.zeros(num_outputs, requires_grad=True) #定义一个Softmax def softmax(X): X_exp = torch.exp(X) partition = X_exp.sum(1, keepdim=True) return X_exp / partition # 这里应用了广播机制 #定义网络模型 def net(X): #使用 torch.matmul() 函数计算输入数据 X 与权重 W 的矩阵乘法。 #将偏置 b 加到上述结果中。 #将结果应用 softmax 函数。 #256 * 784 return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b) #定义交叉熵损失函数 def cross_entropy(y_hat, y): return - torch.log(y_hat[range(len(y_hat)), y]) #将预测类别y_hat与真实y元素进行比较 def accuracy(y_hat, y): """计算预测正确的数量""" if len(y_hat.shape) > 1 and y_hat.shape[1] > 1: #axis=1 表示沿着第一个维度(通常是行)进行操作 #y_hat.argmax返回一个一维张量,其中每个元素是对应样本的最大值的索引 y_hat = y_hat.argmax(axis=1) #张量 y_hat 里的数据类型是否与张量 y 里的数据类型相同,并将结果存储在 cmp 变量中 cmp = y_hat.type(y.dtype) == y return float(cmp.type(y.dtype).sum()) #cmp.type(y.dtype) 将张量 cmp 中的数据类型转换为与张量 y 相同的数据类型。这是为了确保类型匹配。 #.sum() 对张量中的所有元素进行求和操作。由于 True 在数值上等价于 1,而 False 在数值上等价于 0,因此求和操作将计算出 cmp 中值为 True 的元素的数量。 #float() 将计算结果转换为浮点数类型。 #这个结果通常用于计算模型预测的准确率,即模型正确预测的样本数量与总样本数量的比例。 #可以评估在任意模型net的准确率 def evaluate_accuracy(net, data_iter): """计算在指定数据集上模型的精度""" if isinstance(net, torch.nn.Module): net.eval() # 将模型设置为评估模式 在评估模式下,模型不会进行参数更新 metric = Accumulator(2) # 正确预测数、预测总数 with torch.no_grad():#一个上下文管理器,它指示 PyTorch 在接下来的代码块中不要进行梯度计算 for X, y in data_iter:#遍历 data_iter 中的数据。在每次迭代中,X 是输入特征的批量,y 是对应的标签。 metric.add(accuracy(net(X), y), y.numel()) #神经网络模型 net 对输入数据 X 进行前向传播,得到预测结果。然后使用 accuracy 函数计算预测结果的准确率。接着调用 metric 对象的 add 方法,将准确率和当前批量数据的样本数量 y.numel() 作为参数传入,用于累积这些值。这样可以在整个评估过程中跟踪模型的平均准确率 return metric[0] / metric[1] #Softmax回归训练,训练模型一个迭代周期 def train_epoch_ch3(net, train_iter, loss, updater): #@save """训练模型一个迭代周期(定义见第3章)""" # 将模型设置为训练模式 if isinstance(net, torch.nn.Module): net.train() # 训练损失总和、训练准确度总和、样本数 metric = Accumulator(3) for X, y in train_iter: # 计算梯度并更新参数 y_hat = net(X) l = loss(y_hat, y)#交叉熵损失函数 if isinstance(updater, torch.optim.Optimizer): # 使用PyTorch内置的优化器和损失函数 updater.zero_grad()#梯度置为0 l.mean().backward()#计算损失函数 l 对模型参数的梯度 updater.step()#计算梯度后,调用优化器的 step() 方法来更新模型的参数 else: # 使用定制的优化器和损失函数 l.sum().backward() updater(X.shape[0]) metric.add(float(l.sum()), accuracy(y_hat, y), y.numel()) # 返回训练损失和训练精度 return metric[0] / metric[2], metric[1] / metric[2] #训练函数 def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater): #@save """训练模型(定义见第3章)""" animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9], legend=['train loss', 'train acc', 'test acc']) for epoch in range(num_epochs): #使用训练数据集,训练一个周期 train_metrics = train_epoch_ch3(net, train_iter, loss, updater) #使用测试数据集,评价精度 test_acc = evaluate_accuracy(net, test_iter) #将当前周期的训练指标和测试准确率添加到动画器中,以便可视化 animator.add(epoch + 1, train_metrics + (test_acc,)) train_loss, train_acc = train_metrics#将训练指标解包,得到训练损失和训练准确率。 assert train_loss < 0.5, train_loss assert train_acc <= 1 and train_acc > 0.7, train_acc assert test_acc <= 1 and test_acc > 0.7, test_acc #小批量随机梯度下降来优化模型的损失函数 lr = 0.1 def updater(batch_size): return d2l.sgd([W, b], lr, batch_size) #训练模型10个迭代周期 num_epochs = 10 train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
6.Softmax回归的简介实现
import torch from torch import nn from d2l import torch as d2l batch_size = 256 train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size) #初始化模型参数 # PyTorch不会隐式(自动)地调整输入的形状。因此, #创建了一个简单的神经网络模型 net #nn.Flatten(): 这是一个用于将输入数据展平的层,将输入的多维数据(比如图像)展平成一维向量 # nn.Linear这是一个全连接层,将输入的 784 维向量映射到一个 10 维的输出向量。 net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10)) def init_weights(m):#接受一个参数 m if type(m) == nn.Linear:#检查当前层 m 是否为线性层 (nn.Linear) nn.init.normal_(m.weight, std=0.01)#如果是线性层,则使用正态分布(normal distribution)随机初始化该层的权重 m.weight,标准差为 0.01 net.apply(init_weights);#将定义的 init_weights 函数应用到神经网络模型 net 的所有层上,以便对每一层的权重进行初始化操作 #在交叉熵损失函数中传递未归一化的预测,并同时计算Softmax及其对数 loss = nn.CrossEntropyLoss(reduction='none') #使用学习率为0.1的小批量随机梯度下降作为优化算法 trainer = torch.optim.SGD(net.parameters(), lr=0.1) #训练 num_epochs = 10 d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/从前慢现在也慢/article/detail/716931
推荐阅读
相关标签



