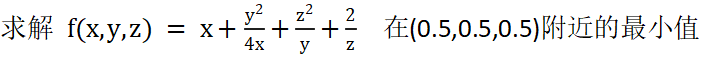devbox
小蓝xlanll
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

第二天：非线性规划(nonlinear programming)_fmincon stopped because it exceeded the function e

作者：小蓝xlanll | 2024-06-16 23:43:20

赞

踩

fmincon stopped because it exceeded the function evaluation limit,

目录：

        一、非线性规划介绍

        二、matlab中非线性规划函数

                1.fminbnd——求解一维函数 

                2.fminsearch——求解无约束多维极值问题

                3.fminimax——求解最大最小值(多目标)问题

                4.fminunc——求解无约束多维极值问题

                5.fmincon——约束优化问题

        三、启发式算法介绍

                1.模拟退火算法(SA,Simulated Annealing)

                2.神经网络算法(NN,Neural Network)

                3.蚁群算法(ACO,Ant Clony Optimization)

一、非线性规划介绍

        线性规划的目标函数与约束条件都是线性的，如果目标函数与约束条件中包含有非线性因素存在，则这样的规划问题就被称为非线性规划问题。其实，规划问题可以简单粗暴的一分为二，不是线性就是非线性。在实际的问题中，非线性规划的比率较高，今天学习的非线性规划也仅仅作为一个简单的入门。

        非线性规划的一般数学表示形式为：

                                                                min f(X)

                                            st.                h(X)=0

                                                                g(X)>=0

与线性规划的数学形式一致

二、matlab中的内置非线性规划函数

        matlab中的内置非线性规划函数在其工具箱Optimization Toolbox中均有对应的功能，介绍函数后我们可以直接使用工具箱来进行求解。

1.fminbnd——求解一维函数

[x,fx,exitflag,output]=fminbnd(fun,lb,ub,options)

输出参量分析：

x:最小值点

fx:最小值

exitflag:输出算法停止原因

             若1，则已寻找到最优解

             若0，迭代次数超过设置的迭代次数

             若-2，则输入的lb,ub错误

output:一个struct字段，包含三项信息

              interations:迭代次数

              funcCounnt:函数赋值次数

             algorithm:使用算法

输入参量分析：

fun:输入的函数，以'fun'或@fun的形式输入

lb,ub:解的可行域

options:options是对求解过程中的迭代次数，终止容差(我理解的是解的精度)，以及是否做出迭代图像的控制。options的设置要使用optimset函数

以一段具体代码来分析：

  1. options = optimset('Display','iter');          %显示迭代过程。
  2. options = optimset('PlotFcns',@optimplotfval); %绘制迭代图。
  3. options = optimset('Tolx',1e-6)；              %设置解的容差
  4. options = optimset('MaxIter',1000)；           %设置最大迭代次数

这里以matlab内置humps函数演示

humps图像如图 

ezplot(@humps,[0 2])

 取解的范围为[0.2 1]

  1. clear all
  2. clc
  3. lb = 0.2;                                      %规定解的可行域
  4. ub = 1;
  5. options = optimset('Display','iter');          %显示每一步的迭代结果
  6. options = optimset('PlotFcns',@optimplotfval); %绘制迭代图。
  7. options = optimset('Tolx',1e-6);               %设置解的容差
  8. format long
  9. [x,fx,exitflag,output]=fminbnd(@humps,lb,ub,options)

运行结果：

  1. x =
  2.  
  3.    0.637008945968909
  4.  
  5.  
  6. fx =
  7.  
  8.   11.252754125696612
  9.  
  10.  
  11. exitflag =
  12.  
  13.      1
  14.  
  15.  
  16. output = 
  17.  
  18.   包含以下字段的 struct:
  19.  
  20.     iterations: 10
  21.      funcCount: 11
  22.      algorithm: 'golden section search, parabolic interpolation'
  23.        message: '优化已终止:↵ 当前的 x 满足使用 1.000000e-06 的 OPTIONS.TolX 的终止条件↵'

由于只能求一维函数极值，因此fminbnd函数的应用(比如解一些高中数学题?）并不多，但通过对fminbnd函数的使用却能让我们学会options的设置以及明白各项输出结果所代表的意义。

2.fminsearch——求解无约束多维问题

        fminsearch是用来求解无约束条件的多维极值函数，其调用方式为：

                        [x,fx,exitflag,output]=fminsearch(fun,x0,options)

输出输入参量的意义同上，其中x0为给定初始解。

matlab代码实现

  1. function f=fun(x)        %建立函数的.m文件
  2. f=x(1)+x(2)^2/(4*x(1))+x(3)^2/x(2)+2/x(3);
  3. end
  4.  
  5. clear all
  6. clc
  7. options = optimset('Display','iter');          %显示每一步的迭代结果
  8. options = optimset('Tolx',1e-6);              %设置解的容差
  9. [x,fx,exitflag,output]=fminsearch(@fun,[0.5 0.5 0.5],options)

 运行结果：

  1. x =
  2.  
  3.    0.499999856353490   0.999999396261153   0.999999673629114
  4.  
  5.  
  6. fx =
  7.  
  8.    4.000000000000340
  9.  
  10.  
  11. exitflag =
  12.  
  13.      1
  14.  
  15.  
  16. output = 
  17.  
  18.   包含以下字段的 struct:
  19.  
  20.     iterations: 97
  21.      funcCount: 174
  22.      algorithm: 'Nelder-Mead simplex direct search'
  23.        message: '优化已终止:↵ 当前的 x 满足使用 1.000000e-06 的 OPTIONS.TolX 的终止条件，↵F(X) 满足使用 1.000000e-04 的 OPTIONS.TolFun 的收敛条件↵'

fminsearch函数的缺点也很明显，就是只能求出来距离初始解不太远的解，fminsearch太过依赖初始解的选择，比如，还是这个函数，如果换一个初始解

  1. clear all
  2. clc
  3. options = optimset('Display','iter');          %显示每一步的迭代结果
  4. options = optimset('Tolx',1e-6);               %设置解的容差
  5. options = optimset('MaxIter',10000);           %最大迭代次数 
  6. options = optimset('MaxFunEvals',10e30);       %运算过程f的最大值
  7. [x,fx,exitflag,output]=fminsearch(@fun,[10 5 6],options)
  8.

这次将初始解换成了[10 5 6]

运行结果：

  1. 正在退出: 超过了最大迭代数
  2.  - 请增大 MaxIter 选项。
  3.  当前函数值: -135597917695371366357767467343187646703088724606976.000000 
  4.  
  5.  
  6. x =
  7.  
  8.    -2.1612   -3.2299   -0.0000
  9.  
  10.  
  11. fx =
  12.  
  13.   -1.3560e+50
  14.  
  15.  
  16. exitflag =
  17.  
  18.      0
  19.  
  20.  
  21. output = 
  22.  
  23.   包含以下字段的 struct:
  24.  
  25.     iterations: 600
  26.      funcCount: 1169
  27.      algorithm: 'Nelder-Mead simplex direct search'
  28.        message: '正在退出: 超过了最大迭代数↵ - 请增大 MaxIter 选项。↵ 当前函数值: -135597917695371366357767467343187646703088724606976.000000 ↵'

误差挺大的。

3.fminimax——求解最大最小值问题

        fminimax用来求解: min max(f(x))

                        st.           A*x<=b                

                                       Aeq*x=beq

                                       C(x)<=0

                                       Ceq(x)=0

                                       lb<=x<=ub

具体的使用方式如下：

[x,fx,maxfx,exitflag,output]=fminimax(@fun,x0,A,b,Aeq,beq,lb,ub,@nonlone,options)

fun的输出为向量或矩阵

里面输入输出信息详见 第一天：线性规划（linear programming)

如果没有非线性约束即没有@nonlone函数，则用[]代替其位置，则fminimax就变成了一个求线性规划的多目标问题函数。

这里面的@nonlone函数，这是一个非线性约束的函数，编写格式如下

  1. function [C,Ceq]=nonlone(x)
  2. for i=1:n                    %这一段代码是我偷懒了，这一段是用于理解的代码，不是实际代码
  3.     C(i)=K[i](x)             %其实我的意思是，非线性约束条件有n个，每一个约束对应的函数为K[i]
  4. end                          %C(i)即为第i个约束K[i](x)对应的值
  5. for i=1:m                    %下同理
  6.     Ceq(i)=G[i](x)
  7. end
  8. end

用一个例子应该能更好的帮助理解：

比如：非线性不等式约束：x^2-y<=0;                        

                                           x^2+y^2<=10;

            线性约束：x+y=0;

则可编写函数文件

  1. function [C,Ceq]=nonlone(x)
  2. C(1)=x(1)^2-x(2);
  3. C(2)=x(1)^2+x(2)^2-10;
  4. Ceq=x(1)-x(2);
  5. end

fminimax可以用例子更好的去理解：

假设鸟儿要建一个自己的巢，现给定一些被鸟儿捕食生物的坐标，假定在鸟儿的一生中这些被捕食生物的坐标不变，且次日可再生(即被捕时后在次日有下一个被捕食生物替补过去)，每个点的食物数量相同。现在鸟儿应当选择一个位置筑巢，以保证每天可以尽可能多吃少动。我们假设鸟儿可选择筑巢的位置坐标是连续的。

现给定20个被捕时者的位置坐标

25130
40470
354915
71546
161748
21414
27230
269713
37130
103114
171915
274712
67130
36480
571317
484142
38123
2230
42310
14230

鸟儿可以选择筑巢的范围为lb=[10 10 10],ub=[49 45 36];已知鸟儿一次可活动的范围为30，每次活动捕食一次后返回。每天须捕食10次。  

matlab代码实现：

  1. function f=fun(x) 
  2. %计算三维空间距离的函数
  3. c=[25	13	0
  4. 40	47	0
  5. 35	49	15
  6. 7	15	46
  7. 16	17	48
  8. 21	4	14
  9. 27	23	0
  10. 26	97	13
  11. 37	13	0
  12. 10	31	14
  13. 17	19	15
  14. 27	47	12
  15. 67	13	0
  16. 36	48	0
  17. 57	13	17
  18. 48	41	42
  19. 38	1	23
  20. 2	23	0
  21. 42	31	0
  22. 14	23	0];
  23. for i=1:20
  24.     f(i)=sqrt((x(1)-c(i,1))^2+(x(2)-c(i,2))^2+(x(3)-c(i,3))^2);
  25. end
  26. end
  1. function [C,Ceq]=nonlcon(x)
  2. f=fun(x);
  3. [a,b]=size(find(f<=30));  %获取距离小于50的个数
  4. C=10-a*b;
  5. Ceq=[];
  6. end
  1. clear all
  2. clc
  3. c=[25	13	0           %导入坐标
  4. 40	47	0
  5. 35	49	15
  6. 7	15	46
  7. 16	17	48
  8. 21	4	14
  9. 27	23	0
  10. 26	97	13
  11. 37	13	0
  12. 10	31	14
  13. 17	19	15
  14. 27	47	12
  15. 67	13	0
  16. 36	48	0
  17. 57	13	17
  18. 48	41	42
  19. 38	1	23
  20. 2	23	0
  21. 42	31	0
  22. 14	23	0];
  23. %画出初始坐标
  24. scatter3(c(:,1),c(:,2),c(:,3));
  25. hold on
  26. axis equal
  27. x0=[15 15 15];          %设置初始坐标
  28. A=[];                   %非线性约束
  29. b=[];                   
  30. Aeq=[];                 %线性约束
  31. beq=[];                 
  32. lb=[10 10 10];          %解的上下界
  33. ub=[49 45 36];
  34. %显示迭代过程
  35. options = optimset('Display','iter'); 
  36. [x,fx,maxfx,exitflag,output]=fminimax(@fun,x0,A,b,Aeq,beq,lb,ub,@nonlcon,options);
  37. scatter3(x(1),x(2),x(3),'*','r');

运行结果

  1.  
  2.                   Objective        Max     Line search     Directional 
  3.  Iter F-count         value    constraint   steplength      derivative   Procedure 
  4.     0      5              0       82.7587                                            
  5.     1     11          82.76             1            1               1     infeasible
  6.     2     21          82.82             1       0.0625               1    Hessian modified twice;   infeasible
  7.     3     31          82.88             1       0.0625               1    Hessian modified twice;   infeasible
  8.     4     43           82.9             1       0.0156               1    Hessian modified twice;   infeasible
  9.     5     55          82.91             1       0.0156               1    Hessian modified twice;   infeasible
  10.     6     68          82.92             1      0.00781               1    Hessian modified twice;   infeasible
  11.     7     83          82.92             1      0.00195               1    Hessian modified twice;   infeasible
  12.     8     98          82.93             1      0.00195               1    Hessian modified twice;   infeasible
  13.     9    118          82.93             1     -6.1e-05               1    Hessian modified twice;   infeasible
  14.    10    135          82.93             1     0.000488               1    Hessian modified twice;   infeasible
  15.    11    153          82.93             1     0.000244               1    Hessian modified twice;   infeasible
  16.    12    173          82.93             1     -6.1e-05               1    Hessian modified twice;   infeasible
  17.    13    193          82.93             1     -6.1e-05               1    Hessian modified twice;   infeasible
  18.    14    213          82.93             1     -6.1e-05               1    Hessian modified twice;   infeasible
  19.    15    233          82.93             1     -6.1e-05               1    Hessian modified twice;   infeasible
  20.    16    253          82.93             1     -6.1e-05               1    Hessian modified twice;   infeasible
  21.    17    273          82.93             1     -6.1e-05               1    Hessian modified twice;   infeasible
  22.    18    293          82.93             1     -6.1e-05               1    Hessian modified twice;   infeasible
  23.    19    313          82.93             1     -6.1e-05               1    Hessian modified twice;   infeasible
  24.    20    333          82.93             1     -6.1e-05               1    Hessian modified twice;   infeasible
  25.    21    353          82.93             1     -6.1e-05               1    Hessian modified twice;   infeasible
  26.    22    373          82.93             1     -6.1e-05               1    Hessian modified twice;   infeasible
  27.    23    393          82.93             1     -6.1e-05               1    Hessian modified twice;   infeasible
  28.    24    405          82.94             1       0.0156               1    Hessian modified twice;   infeasible
  29.  
  30. Solver stopped prematurely.
  31.  
  32. fminimax stopped because it exceeded the function evaluation limit,
  33. options.MaxFunctionEvaluations = 4.000000e+02.
  34.  
  35.  
  36. x =
  37.  
  38.     15    15    15
  39.  
  40.  
  41. fx =
  42.  
  43.   列 1 至 13
  44.  
  45.    18.1384   43.2897   39.4462   32.0156   33.0757   12.5698   20.8087   82.7587   26.7021   16.7929    4.4721   34.3074   54.1572
  46.  
  47.   列 14 至 20
  48.  
  49.    41.8927   42.0951   49.9400   28.0891   21.4009   34.7851   17.0294
  50.  
  51.  
  52. maxfx =
  53.  
  54.    82.7587
  55.  
  56.  
  57. exitflag =
  58.  
  59.      0
  60.  
  61.  
  62. output = 
  63.  
  64.   包含以下字段的 struct:
  65.  
  66.          iterations: 24
  67.           funcCount: 405
  68.        lssteplength: 0.0156
  69.            stepsize: 0.0156
  70.           algorithm: 'active-set'
  71.       firstorderopt: []
  72.     constrviolation: 1
  73.             message: '↵Solver stopped prematurely.↵↵fminimax stopped because it exceeded the function evaluation limit,↵options.MaxFunctionEvaluations = 4.000000e+02.↵↵'


4.fminunc——求解无约束多维极值问题

        fminunc的用法同fminsearch相似，也是求多维无约束极值问题，使用方法为：

                [x,fx,exitflag,output]=fminunc(@fun,x0,options)

5.fmincon——约束优化问题

一般约束优化问题的数学模型为 min f(x)

                                                   st.     h[i](x)=0,     i=1,2,...,k

                                                             g[j]<=0,       j=1,2,...,m

fmincon实现约束优化问题：

        [x,fx,exitflag,output]=fmincon(@fun,x0,A,b,Aeq,beq,lb,ub,@nonlcon,options)

输出输入的参数依旧和前面相同

例：min f(s,t)=s^4-4*s-8*t+15

st. 9-s^2-t^2<=0

     2*s+3*t<=2

     t-s<=5

matlab代码实现：

  1. function f=fun(x) 
  2. s=x(1);
  3. t=x(2);
  4. f=s^4-4*s-8*t+15;
  5. end
  1. function [C,Ceq]=nonlcon(x)
  2. C=9-x(1)^2-x(2)^2;
  3. Ceq=[];
  4. end
  1. clear all
  2. clc
  3. x0=[1 3];                            %初始解可以任意取
  4. A=[2,3;1,-1];                        %不等式约束
  5. b=[2,5];
  6. Aeq=[];                              %等式约束
  7. beq=[];
  8. lb=[];                               %解的可行域
  9. ub=[];
  10. options = optimset('Display','iter');%显示迭代过程
  11. options = optimset('PlotFcns',@optimplotfval); %绘制迭代图
  12. [x,fx,exitflag,output]=fmincon(@fun,x0,A,b,Aeq,beq,lb,ub,@nonlcon,options)

运行结果：

  1. x =
  2.  
  3.    -2.1454    2.0969
  4.  
  5.  
  6. fx =
  7.  
  8.    27.9925
  9.  
  10.  
  11. exitflag =
  12.  
  13.      1
  14.  
  15.  
  16. output = 
  17.  
  18.   包含以下字段的 struct:
  19.  
  20.          iterations: 9
  21.           funcCount: 33
  22.     constrviolation: 0
  23.            stepsize: 2.0058e-06
  24.           algorithm: 'interior-point'
  25.       firstorderopt: 3.7132e-05
  26.        cgiterations: 0
  27.             message: '↵Local minimum found that satisfies the constraints.↵↵Optimization completed because the objective function is non-decreasing in ↵feasible directions, to within the value of the optimality tolerance,↵and constraints are satisfied to within the value of the constraint tolerance.↵↵<stopping criteria details>↵↵Optimization completed: The relative first-order optimality measure, 8.535931e-07,↵is less than options.OptimalityTolerance = 1.000000e-06, and the relative maximum constraint↵violation, 0.000000e+00, is less than options.ConstraintTolerance = 1.000000e-06.↵↵'

启发式算法求解非线性函数

        上述介绍的matlab内置函数可以解决连续的优化问题，但遇到离散的优化却无能为力，比如旅行商问题(TSP,traveling salesman problem)，聚类问题(clustering problem)，加工调度问题(scheduling problem)，背包问题(knapsack problem)和着色问题(graph coloring problem)。经典的算法无法解决这些问题，这时就需要一种新的算法来解决这种问题。人们从大自然的运行规律中找到了许多解决实际问题的方法。对于那些受大自然的运行规律或者面向具体问题的经验、规则启发出来的方法，人们称之为启发式算法(heuristic algorithm,HA)。

        Holland模拟达尔文生物进化论的自然选择与遗传学机理的生物进化过程提出了遗传算法(genetic algorithm,GA)，通过模拟自然进化过程搜索最优解。此后，模拟退火算法(SA,Simulated Annealing)，神经网络算法(BP,Back Propagation)，禁忌搜索(TS,Tabu Search)相继出现，接着，进化算法(EA,Evolutionary Algorithms)，蚁群算法(ACO,Ant Clony Optimization)，拟人拟物算法和量子算法等相继出现。

        由于精力有限，我只学习了模拟退火、神经网络，蚁群算法，之后我会再开一个专栏(因为一天实在学不完，呜呜呜)专门介绍这些算法的具体实现，在此我就简单介绍一下算法基本简介。如果后面再学其它算法的话，我会再加上。

1.模拟退火算法(SA,Simulated Annealing)

        模拟退火算法(SA,Simulated Annealing)来源于固体退火原理，是一种基于概率的算法，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温度升高而变得无序，内能增大，而徐徐冷却时的粒子(解)渐趋有序，在每个温度都达到平衡状态(多次内部迭代)，最后在常温(设定)时达到基态，内能减为最小。

        模拟退火算法最早的思想是由Metropolis等人于1953年提出。1983年，Kirkpatrick成功的将退火思想引入到组合优化领域。模拟退火算法是基于Monte-Carto迭代求解策略的一种随机寻优算法。模拟退火算法从某一较高温度出发,伴随温度参数而不断下降，结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即可行解能以一定概率性跳出局部最优，理算法具有概率的全局最优性能。

        

2.神经网络算法(Neural Network NN)

        神经网络是一种类似于人脑神经突触连接的结构进行信息处理的数学模型，它是对人脑的抽象、简化和模拟，反映人脑的基本特性。

        神经网络有大量的节点(也可称之为神经元或单元)和相互之间的加权连接构成，每一个连接都代表一个特定的输出函数，称为激励函数(activation function)。每两个节点间的连接都代表一个对于通过该连接信号的加权值，称之为权重(weight)，这相当于神经网络的记忆。网络的输出则根据网络的连接方式、权重值和激励函数的不同而不同。而神经自身通常都是对自然界某种算法的逼近或者函数的逼近，也可以是对一种逻辑策略的表达。

        神经网络系统涉及的方面太广，神经网络是一种深度的机器学习，感觉用神经网络来解决非线性规划有点杀鸡用牛刀的意思。这个东西以我现在的能力还无法很快很好的理解，估计下次提到它要很久之后了。

PS:看着一本本厚厚的神经网络书籍我就头大。

3.蚁群算法(ACO,Ant Clony Optimization)

        意大利学者Dorigo等研究人员受到自然界中蚁群搜索食物最短路径行为规律的启发。于1991年在法国巴黎召开的第一届欧洲人工生命会议(European Conference on Artificial Life,ECAL)上提出了蚁群优化算法(ACO,Ant Clony Optimization)的核心思想。蚁群算法是一种启发式算法，蚁群学习获得启发式值的解决方案，并且利用启发式信息促使搜索过程向着高质量的近似解发展。

        信息素引导蚂蚁移动轨迹的选择。蚂蚁在寻找食物的途中，一方面在所选择的路径上释放信息素，另一方面也需要分析其它蚂蚁释放的信息素。这样，有许多蚂蚁所组成的蚁群释放的信息素

将蚂蚁关联起来，促成了蚂蚁之间的沟通和互相合作。通过较短路径找到食物的蚂蚁返回巢穴所用的时间较少，在相同时间内其路径上积累的信息素就较多，提高了后续蚂蚁选择这条路径的概率，该路径最终会成为蚁群的最优路径。

        蚁群算法应用于解决优化问题的基本思路为：用蚂蚁的行走路径表示待优化问题的可行解，整个蚂蚁群体的所有路径构成待优化问题的解空间。路径较短的蚂蚁释放的信息素量较多，随着时间的推进，较短的路径上累积的信息素浓度逐渐增高，选择该路径的蚂蚁个数也愈来愈多。最终，整个蚂蚁会在正反馈的作用下集中到最佳的路径上，此时对应的便是待优化问题的最优解。

参考书籍：

1.张德丰.MATLAB R2015b数学建模[M].北京：清华大学出版社，2016

2 孙家泽 王曙燕.群体智能优化算法及其应用[M].北京：科学教育出版社，2017.6

3.朱凯 王正林.精通MATLAB神经网络[M].北京：电子工业出版社，2010.1

本文内容由网友自发贡献，转载请注明出处：https://www.wpsshop.cn/w/小蓝xlanll/article/detail/728770
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号