数据结构----各种排序方法总结_数据结构排序的五种方法

数据结构----各种排序方法总结

提示：数据结构中的排序方法包括插入排序

一、插入排序

插入排序的定义：在有序序列中插入一个元素，保持序列有序，有序长度不断增加

1.直接插入排序

利用图形理清思路

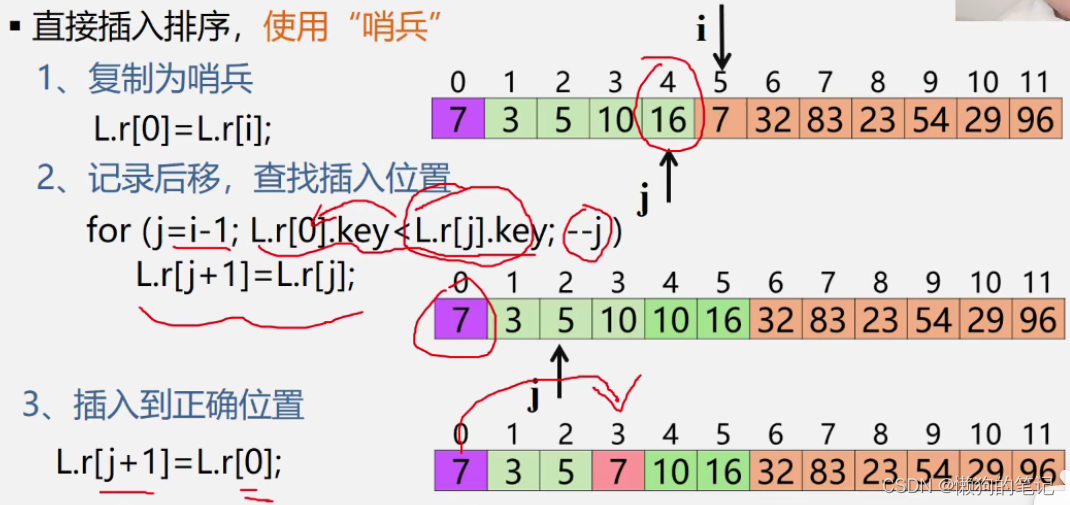
void InsertSort(int a[], int n) {
	//在直接插入排序中，使用0号位置作为哨兵，用于暂时存放当前要插入的元素
	int i, j;
	for (i = 2; i <= n; i++) {
		//当前要插入的元素比前一个元素小时才要进行比较
		if (a[i] < a[i - 1]) {  
			a[0] = a[i];
			for (j = i - 1;a[0]<a[j]; j--) {
				a[j + 1] = a[j];  //数组的长度增加，元素后移
			}
			a[j + 1] = a[0];  //插入到正确的位置
		}
	}
 }
1
2
3
4
5
6
7
8
9
10
11
12
13
14

2.折半插入排序

折半插入排序的思想与直接插入排序的思想是差不多的，只是在查找当前要插入的元素的位置时采用了二分查找的方法，其他部分与直接插入查找一样。

void BinInsertSort(int a[], int n) {
	int low, high,mid;
	int i, j;
	//int temp;
	for (i = 2; i <= n; i++) {
	    a[0]=a[i];
		low = 1;
		high = i - 1;
		//使用二分查找的方法查找当前元素应该在有序序列中的哪一个位置
		while (low <= high) {
			mid = (low + high) / 2;
			if (a[mid] < a[0]) {
				low = mid + 1;
			}
			else {
				high = mid - 1;
			}
		}
		for (j = i-1; j > low; j--) {
			a[j + 1] = a[j];
		}
		a[low] = a[0];
	}
	for (int i = 1; i <= n; i++) {
		cout << a[i] << " ";
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

3.希尔插入排序

希尔插入排序与直接插入排序的方法是一样的，不过希尔插入排序的间隔是变化的，不恒为1，下图可以帮助我们理解希尔插入排序工作的原理：

void ShellSort(int a[], int n, int dk) {
	int i, j;
	//代码的思路都和直接插入排序类似，只不过间隔不恒为1
	for (i = dk + 1; i <= n; i++) {
		a[0] = a[i];
		if (a[i] < a[i - dk]) {
			for (j = i - dk; a[0] < a[j]; j = j - dk) {
				a[j + dk] = a[j];
			}
			a[j + dk] = a[0];
		}
	}	
}

//希尔排序
void ShellInsertSort(int a[], int n, int dlk[], int t) {
   //dlk[]数组表示增量序列，增量序列是不唯一的
	for (int i = 0; i < t; i++) {
		ShellSort(a,n, dlk[i]);
	}	
}

/*
用希尔插入排序的效率是与增量序列的取值有关的，希尔排序也是一种不稳定的排序方法。目前还没有办法获取一个最佳的增量序列，但是可以确定的是增量序列的最后一个元素必须为1，并且所有元素除了1无其他公因子
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

二、交换排序

1.冒泡排序

：

//冒泡排序
void bubble_sort(int a[], int n) {
	int i, j;
	int temp;
	for (i = 1; i <= n-1; i++) {
		for (j = 0;j<= n - i-1; j++) {
			if (a[j] > a[j + 1]) {
				temp = a[j];
				a[j] = a[j + 1];
				a[j + 1] = temp;
			}
		}
	}
	for (int i = 0; i < n; i++) {
		cout << a[i] << " ";
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

改进后的冒泡排序

//改进的冒泡排序
void BubbleSort(int a[], int n) {
	int i, j;
	int temp;
	int flag = 1;  //作为是否有交换的标志
	for (i = 1; i <= n - 1 && flag==1; i++) {
		flag = 0;
		for (j = 0; j <= n - i - 1; j++) {
			if (a[j] > a[j + 1]) {
				temp = a[j];
				a[j] = a[j + 1];
				a[j + 1] = temp;
				flag = 1;   //若发生交换，那么下一趟就要比较；若本趟没有发生交换，则说明数组已经排好了
			}
		}
	}
	for (i = 0; i < n; i++) {
		cout << a[i] << " ";
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

2.快速排序

快速排序不适合有序或者基本有序的序列，序列越乱，那么排序的效率越高。

//快速排序
int Partition(int a[], int n, int low, int high) {
	a[0] = a[low];
	while (low < high) {
		while (low<high && a[high]>=a[0]) {
			high--;
		}
		a[low] = a[high];
		while (low < high && a[low] <= a[0]) {
			low++;
		}
		a[high] = a[low];
	}
	a[low] = a[0];
	return low;
}

void  QuickSort(int a[], int n, int low, int high) {
	if (low >= high) {
		return;
	}
	int mid = Partition(a, n, low, high);
	QuickSort(a, n, low, mid - 1);
	QuickSort(a, n, mid + 1, high);

}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

三、选择排序

1.简单选择排序

图解!

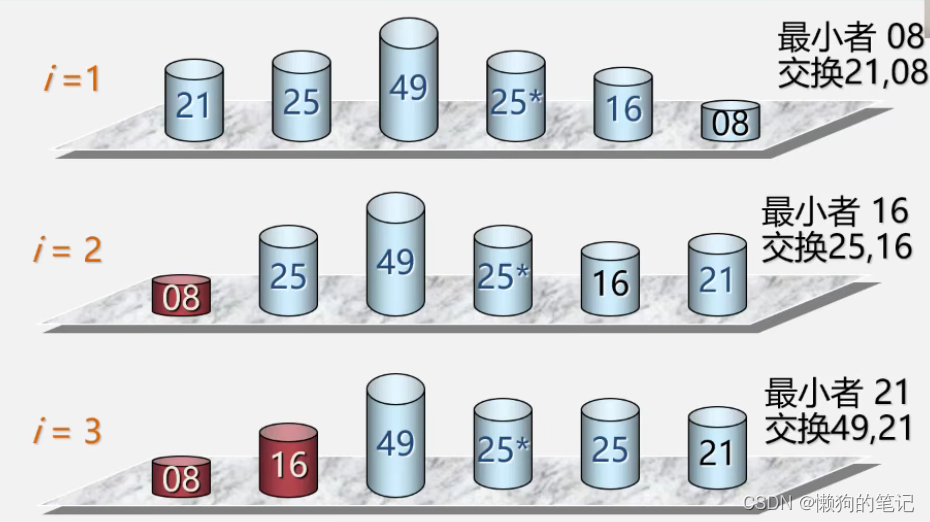
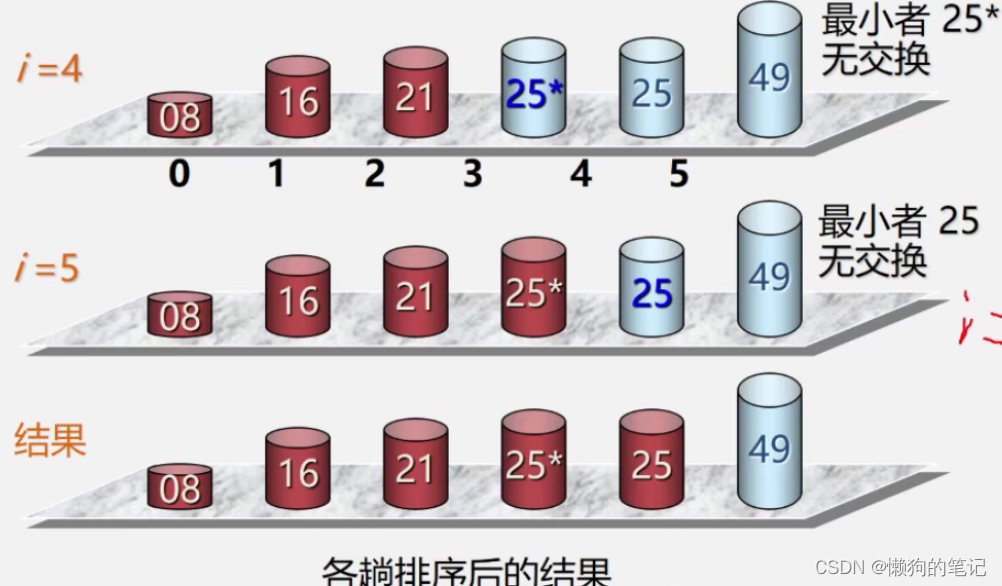
void SelectSort(int a[], int n) {
	int k;
	int x;
	for (int i = 0; i < n-1; i++) {
		k = i;
		for (int j = i+1; j < n; j++) {
			if (a[j] < a[k]) {
				k = j;
			}
		}
		//如果k==i的话就不需要进行交换了
		if (k != i) {
			x = a[i];
			a[i] = a[k];
			a[k] = x;
		}
	}
	for (int i = 0; i < n; i++) {
		cout << a[i] << " ";
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

2.堆排序

堆排序的解题思路：若输出堆顶的最小值（最大值）后，是的剩余的n-1个元素的序列重新建成一个堆，则得到n个元素的次小值（次大值）........如此反复，便能得到一个有序序列，这个过程称之为堆排序。

但是，实现堆排序需要解决两个问题，分别是：
1.如何有一个无序序列建成一个堆？
2.如何在输出堆顶元素后，调整剩余元素为一个新的堆？
下面将逐一解决这两个问题，首先先解决第二个问题，因为第二个问题就相当于第一个问题的子问题
1
2
3
4
5
6

/*
* 如何在输出堆顶元素后，调整剩余元素为一个新的堆？
* 1.输出堆顶之后，以堆中最后一个元素替代
* 2.然后将根结点的值与左右子树的根结点值进行比较，并与其中的大者进行交换；
* 3.重复上述操作，直至叶子结点，将得到新的堆，称这个从堆顶至叶子的调整过程为“筛选”
*/

//将R[s]调整为大根堆
void HeapAdjust(int R[], int s, int m) {
	int rc = R[s];
	//下标从1开始,如果下标从0开始的话，那么j要从2*s+1开始
	for (int j = 2 * s; j <= m; j *= 2) {
		if (R[j] < R[j + 1]) {   //选择左子树与右子树中较小的一个，然后沿着一条路径向下寻找
			j++;
		}
		if (R[j] < rc) {     //如果找到比根结点的值要小的，则停止查找
			break;
		}
		R[s] = R[j];   //否则需要一直查找
		s = j;
	}
	R[s] = rc;   //找到位置后，将此位置的值赋值为根节点的值
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

//如何由一个无序序列建成一个堆？
//下面的例子是建立一个大根堆
void Heap(int R[],int n) {
	//只调整不是叶子结点的结点
	for (int i = n / 2; i >= 1; i--) {
		HeapAdjust(R, i, n);
	}
}
1
2
3
4
5
6
7
8

//堆排序
void HeapSort(int R[], int n) {
	//下标从1开始
	int i;
	int  temp;

	//先建立一个最大堆
	for (i = n / 2; i >= 1; i--) {
		HeapAdjust(R, i, n);
	}
    //每次都使用最后一个结点替代输出堆顶元素后的根结点
	for (i = n; i > 1; i--) {
		temp = R[i];
		R[i] = R[1];
		R[1] = temp;
		//替代后需要重新调整堆
		HeapAdjust(R, 1, i - 1);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

---

四、归并排序

图解：

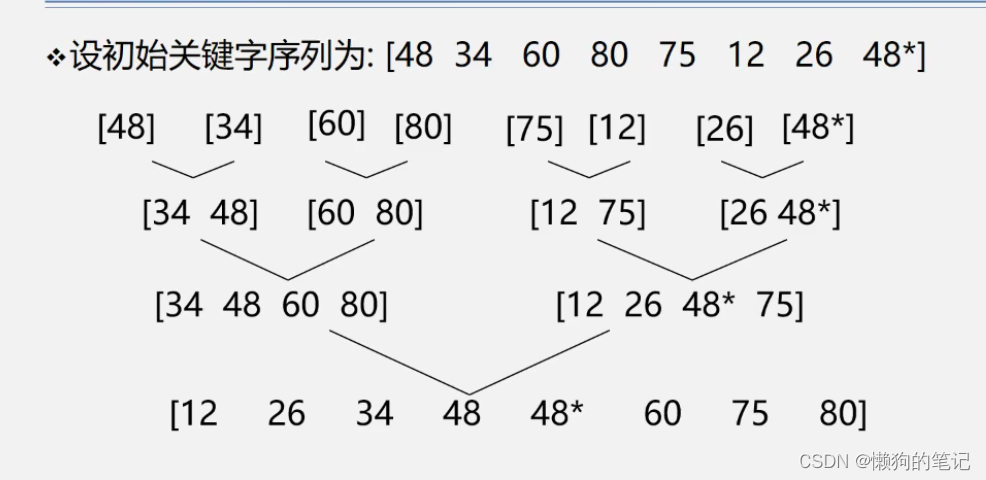
//归并排序
void Merge(int  *a, int start, int mid, int end) {
	int i, j,k=0;
	int* c = new int[end-start+1];
	//a = new int[end - start + 1];
	i = start;
	j = mid + 1;
	while (i <= mid && j <= end) {
		if (a[i] < a[j]) {
			c[k++] = a[i++];
		}
		else {
			c[k++] = a[j++];
		}
	}
	while (i <= mid) {
		c[k++] = a[i++];
	}
	while (j <= end) {
		c[k++] = a[j++];
	}

	for (int s = 0; s < k; s++) {
		a[start + s] = c[s];
	}
	delete[] c;
}
void MergeSort(int a[],int n,int start, int end) {
	if (start >= end) {
		return;
	}
	int mid = (start + end) / 2;

	//下面两个递归是为了将数组进行划分，然后从下往上进行排序
	MergeSort(a, n, start, mid);
	MergeSort(a, n, mid + 1, end);

	Merge(a, start, mid, end);

}


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

五、基数排序

图解

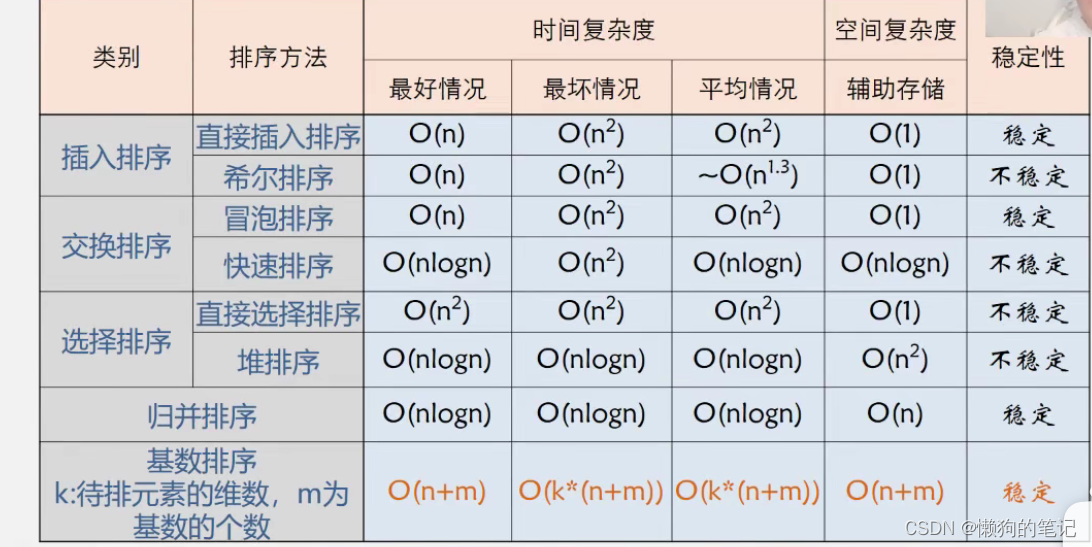
总结

提示：各种排序方法比较