【论文笔记】基于强化学习的机器人手臂仿人运动规划方法_强化学习 机械臂 仿人技能

摘要

【针对问题】人机交互共融环境下仿人机器人的重大需求
【提出方法】一种基于强化学习的机器人手臂仿人运动规划方法
【具体细节】（1）基于结构特征，设计了与人相关的关节角：肩夹角、肘夹角和腕关节；（2）VICON系统对人体运动数据进行分析，获取相关特性；（3）设计不同的回报函数，采用强化学习进行训练（4）搭建仿真平台
【得到效果】仿人运动成功率是$91.25\%$

关键词

1. 人臂运动特性;
2. 仿人运动规划;
3. 强化学习;
4. 运动捕捉系统;

0 引言

机械臂仿人运动的规划主要是从人体手臂出发，分析不同动作状态下的运动特征，并将其应用到机械臂中。

学者研究

阶段一：采集运动数据，分析运动过程特征

阶段二：设计仿人变量、建立仿人标准和约束

【评价】
（1）针对某一类特定任务的仿人运动规划；
（2）仿人变量的设计单一；
（3）仿人参数的选定容易对仿人运动造成影响；

阶段三：用智能算法提升仿人运动机器人性能

【评价】
（1）训练和示教数据不足；
（2）数据模型无法覆盖人体手臂运动模型；
（3）机械臂鲁棒性偏低；

本文工作

1. 采用 VICON 系统获取人臂达点运动数据以保证数据的准确性；
2. 设计肩夹角、肘夹角和腕关节运动角；
3. 正态性和相关性分析获取人体手臂运动特征；
4. 设计不同的回报函数 + 仿人规划（HP）强化学习训练

1 问题描述及方法架构

1.1 人体手臂与机械臂之间的映射关系

将人体手臂运动特征融合到机械臂中是实现机械臂仿人运动的关键
这就要求获取人体手臂与机械臂之间的映射关系

6自由度 Kinova公司 Jaco2机械臂

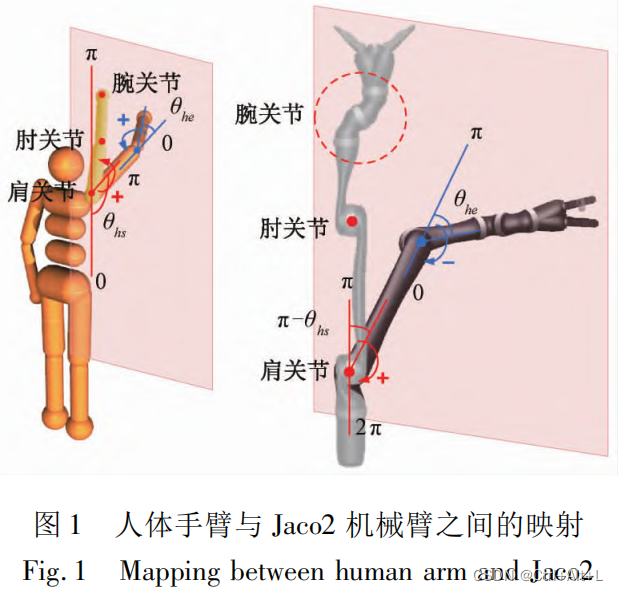
人体手臂肩关节运动了 ${\theta }_{hs}{\theta }_{hs}$ 时，机械臂肩关节对应的角度为 ${\theta }_{js}{\theta }_{js}=(\pi \pi －{\theta }_{hs}{\theta }_{hs})+\pi \pi$。
人体手臂肘关节运动了 ${\theta }_{he}{\theta }_{he}$ 时，机械臂肘关节对应的角度为 ${\theta }_{je}{\theta }_{je}=\pi \pi －{\theta }_{he}{\theta }_{he}$。

仿人运动范围论文：

HU H M，DU J M，HU X H，et al. The experimental research on joint range of motion［M］. Advances in Physical Ergonomics and Human Factors，2016，489: 265-274．
GATES D H，WALTERS L S，COWELEY J，et al. Range of motion requirements for upper-limb activities of daily living［J］. The American Journal of Occupational Therapy，2015，70( 1) : 1-10.

机械臂关节 2 的仿人运动范围为 $[3.438,5.76]rad$
机械臂关节 3 的仿人运动范围为 $[0.559，\pi ]rad$
机械臂关节 1 和腕关节的运动范围为 $[-2\pi ,2\pi ]rad$（本身自身是环转运动）

1.2 整体方法架构

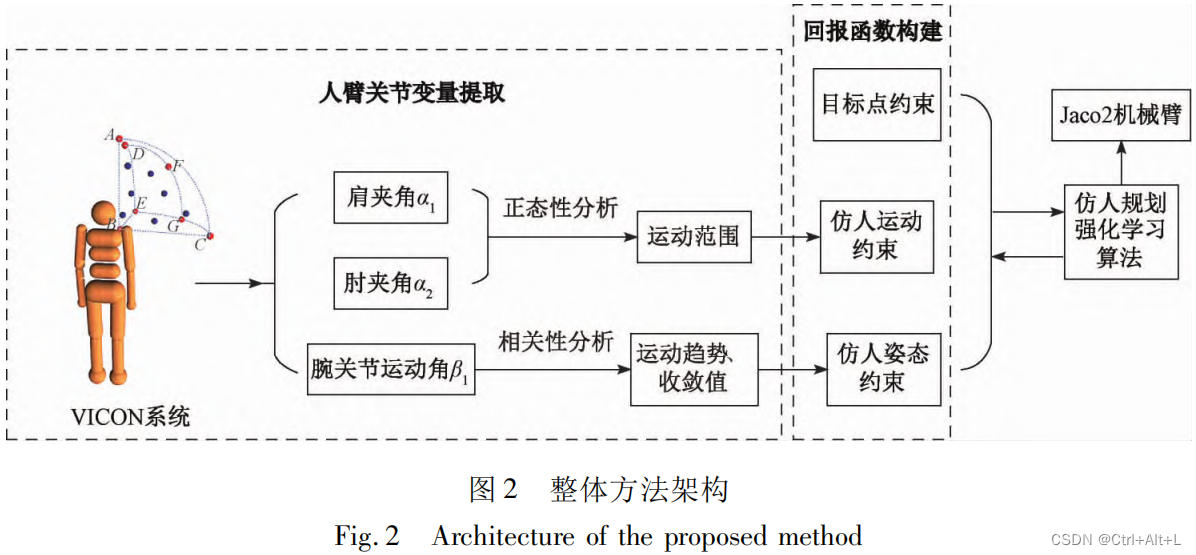
2 手臂运动规律分析与学习

本文采用 VICON 系统采集人体手臂达点运动的数据
获取手臂在达点运动过程中的典型规律和约束。
达点运动：到达目标点的运动。

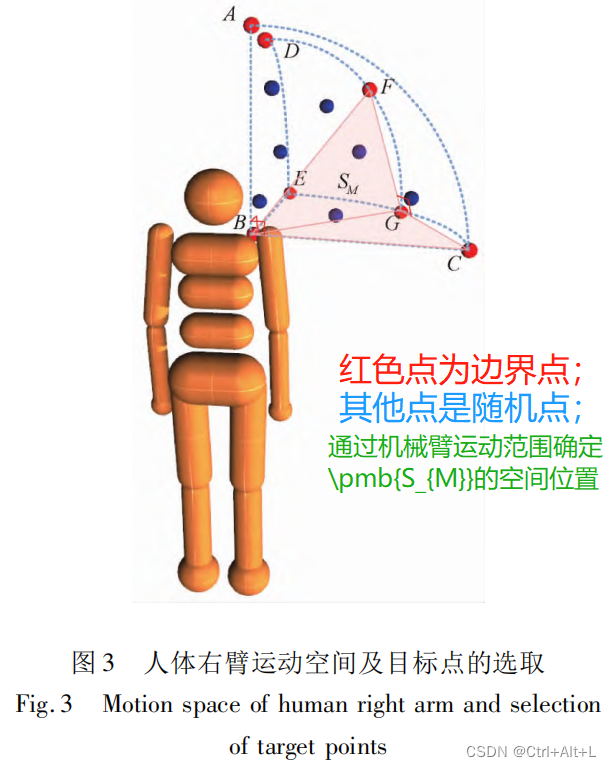
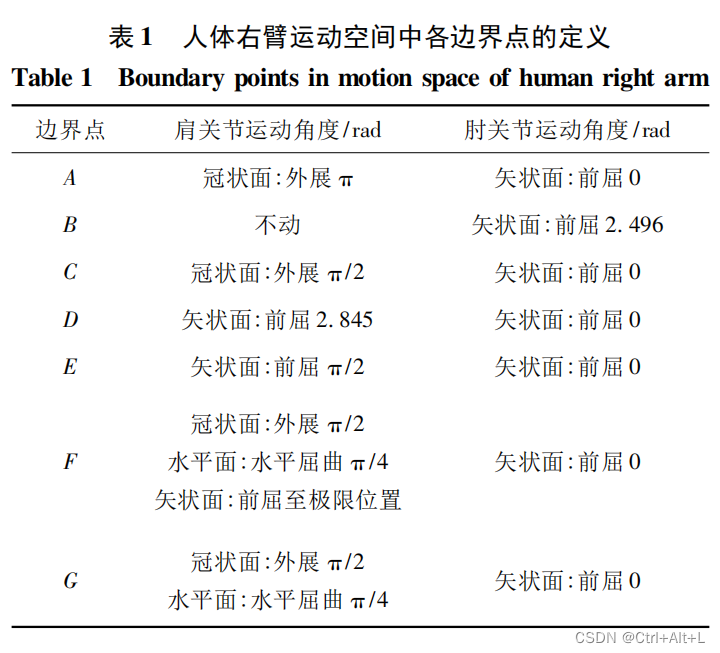
2.1 目标点的选择

本文研究限定范围：人体右臂右半空间中肩关节以上的位置，定义为$S_M{S}_M$

2.2 基于 VICON 的人体手臂运动数据采集方法

1. 设计合适的刚体标志块

设计 3 个刚体标志块（肩膀、上臂和下臂）
由在不同位置下的 4 个相同的反光球构建

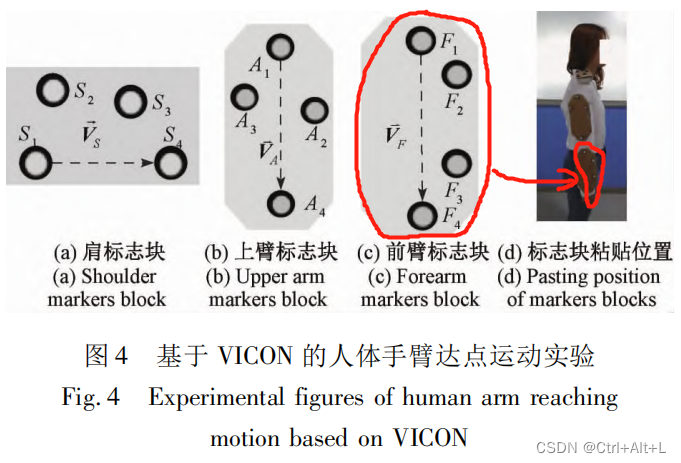
肩向量 $V_S{V}_S$，上臂 $V_A{V}_A$，下臂 $V_F{V}_F$

2. 把各刚体标志块贴于实验者的右臂

3. 收集数据信息

做 100 次达点运动实验，并选用不同的实验者进行实验
手臂的初始位置为自然垂直向下

2.3 人体手臂关节变量构建

1 肩夹角

在人体坐标系 { H } \{ H \} {H}下的坐标
既体现了肩关节的运动情况，还描述了肩部和上臂的运动关系。
{ V S = ( x S 4 − x S 1 , y S 4 − x S 1 , z S 4 − x S 1 ) V A = ( x A 4 − x A 1 , y A 4 − x A 1 , z A 4 − x A 1 ) α 1 = arccos ⁡ ( V S ⋅ V A / ∣ V S ∣ ⋅ ∣ V A ∣ )

$$\begin{cases} \pmb{V_{S}} &= (x_{S4}-x_{S1},y_{S4}-x_{S1},z_{S4}-x_{S1}) \\ \pmb{V_{A}} &= (x_{A4}-x_{A1},y_{A4}-x_{A1},z_{A4}-x_{A1}) \\ \alpha_{1} &= \arccos(\pmb{V_{S}} \cdot \pmb{V_{A}} / |\pmb{V_{S}}|\cdot|\pmb{V_{A}}|) \end{cases}$$ ⎩ ⎨ ⎧​VS​VS​VA​VA​α1​​=(xS4​−xS1​,yS4​−xS1​,zS4​−xS1​)=(xA4​−xA1​,yA4​−xA1​,zA4​−xA1​)=arccos(VS​VS​⋅VA​VA​/∣VS​VS​∣⋅∣VA​VA​∣)​

2 肘夹角

它不仅体现了肘关节的运动情况，还能够描述上臂和前臂的运动关系。
{ V F = ( x F 4 − x F 1 , y F 4 − x F 1 , z F 4 − x F 1 ) α 2 = arccos ⁡ ( V A ⋅ V F / ∣ V A ∣ ⋅ ∣ V F ∣ )

$$\begin{cases} \pmb{V_{F}} &= (x_{F4}-x_{F1},y_{F4}-x_{F1},z_{F4}-x_{F1}) \\ \alpha_{2} &= \arccos(\pmb{V_{A}} \cdot \pmb{V_{F}} / |\pmb{V_{A}}|\cdot|\pmb{V_{F}}|) \\ \end{cases}$$ {VF​VF​α2​​=(xF4​−xF1​,yF4​−xF1​,zF4​−xF1​)=arccos(VA​VA​⋅VF​VF​/∣VA​VA​∣⋅∣VF​VF​∣)​

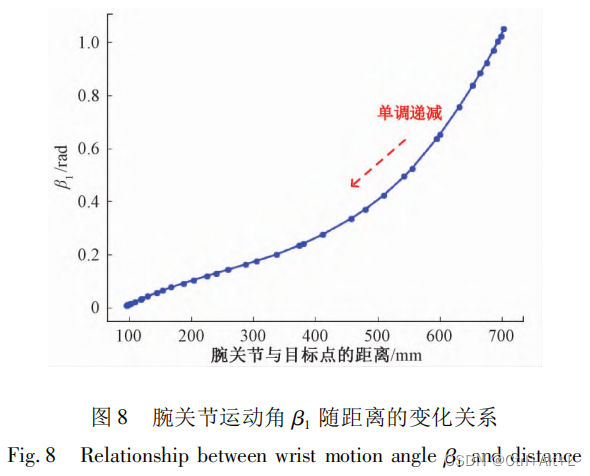
3 腕关节运动角

腕关节与目标点的运动情况。
$${\beta }_1=|\arctan \frac{y_g}{x_g}-\arctan \frac{y_{F4}}{x_{F4}}|$$
${\beta }_w=\arctan \frac{y_{F4}}{x_{F4}}\to$ 腕关节的投影点与坐标原点相连形成的向量和x轴的夹角
${\beta }_g=\arctan \frac{y_g}{x_g}\to$ 目标点$gg=(x_g,y_g,z_g)$与坐标原点相连形成的向量和x轴的夹角

2.4 数据分析与学习

肩夹角 ${\alpha }_1$ 和肘夹角 ${\alpha }_2$ 能够描述人臂运动过程中各部位间的相互关系
因此人臂各部位间的制约关系可以通过 ${\alpha }_1$ 和 ${\alpha }_2$ 的运动范围来体现

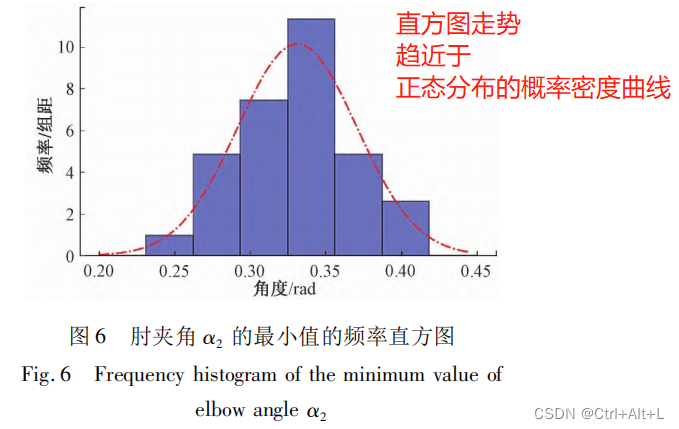
【频率分布直方图】：接近于正态分布

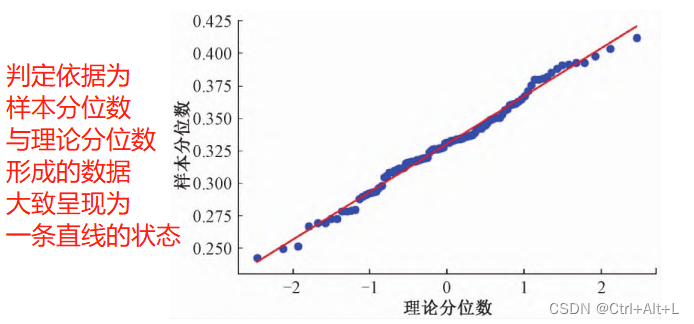
【QQ图】：接近一条直线

QQ图：Quantile-Quantile，接近一条直线说明呈现正态分布的特点

【Shapiro-Wilk 假设检验】

• 一种显著性假设检验方法
• 从统计学意义上将样本分布与正态分布进行比较
• 确定数据是否显示出与正态性的偏离或符合

${\alpha }_2$的最小值是$0.552>0.05=\alpha$（显著性水平）
可以确定与正态分布没有关系

【Spearman 相关系数】

目标点G的斯皮尔曼相关系数为0.996
具备强正相关关系

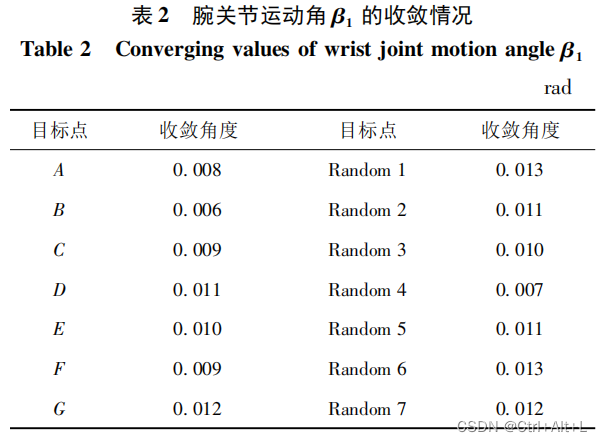
【肩夹角和肘夹角的范围关系确定】

${\alpha }_1\in M_s{M}_s=[0.451,1.385]$ 且 ${\alpha }_2\in M_e{M}_e=[0.138,1.906]$

3 强化学习 HP 算法

Mujoco平台
基于DDPG和HER算法

仿人汇报函数设计

case1：碰撞

若检测到机械臂发生碰撞，则直接结束本回合的训练
将即时回报设置为 $r_t=-100$

case2：机械臂末端的距离

{ d i s = ∣ ∣ ( X E − X G ) × K ∣ ∣ r 1 = { − ln ⁡ ( d i s ) , d i s > 1 0 , d i s ≤ 1

$$\begin{cases} dis &= ||(\pmb{X_{E}-\pmb{X_{G}}})\times\pmb{K}|| \\ r_{1} &= \begin{cases} -\ln(dis)&,dis\gt 1 \\ 0&,dis\le 1 \\ \end{cases}$$ \end{cases} ⎩ ⎨ ⎧​disr1​​=∣∣(XE​−XG​XG​XE​−XG​XG​)×KK∣∣={−ln(dis)0​,dis>1,dis≤1​​
为了避免因单位过大导致的较小的数值变化
将距离信息 $dis$ 的阈值设定为以厘米为单位，即 $KK=100$

cases3：肩夹角和肘夹角是否具备仿人性

$$r_2=-{\omega }_1\cdot \frac{\arctan (\Delta {\alpha }_1)}{\pi /2}-{\omega }_2\cdot \frac{\arctan (\Delta {\alpha }_2)}{\pi /2}$$
$\Delta {\alpha }_1\to$肩夹角范围的偏差
$\Delta {\alpha }_2\to$肘夹角范围的偏差

cases4：腕关节夹角是否具有仿人性

机械臂左右扰动：$r_3=-1$
${\beta }_{1r}\in M_w{M}_w\to$ 具备仿人性 $\to$$r_3=0$
${\beta }_{1r}\notin M_w{M}_w\to$ 不具备仿人性 $\to$$r_3=-\frac{\arctan ({\beta }_{1r})}{\pi /2}$

cases5：都满足上述条件

$r_t=10$

cases6：只有一个不满足

$$\begin{gathered} r_t=\sum _{i=1}^3{\lambda }_i\cdot r_i; \\ {\lambda }_1={\lambda }_2=1; \\ {\lambda }_3=0.5; \end{gathered}$$

归一化措施

4 机械臂仿人运动平台验证及分析

4.1 HP 算法仿真训练

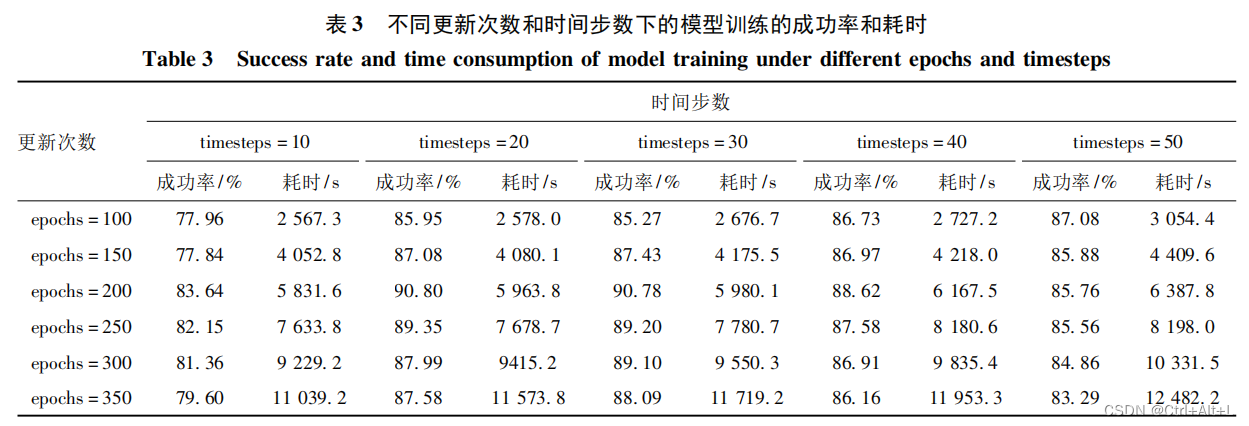
1. 在同一时间步数下，随着更新次数的增加，训练时长明显增加，模型训练的成功率先升高后降低
2. 在同一更新次数下，随着时间步数的增加，训练时长逐渐增加，模型训练的成功率先升高后降低
3. 任务的完成情况受时间步数的影响。（1）过少的时间步数将导致回合内的任务无法完成，从而降低任务的成功率；（2）过多的时间步数则会造成任务的过度拟合，继而产生较差的训练结果。

本文最终将更新次数设为 200，即对应的训练回合数为 10 000，每回合的时间步数设为 20。
随着更新次数的增加，训练的成功率平均为 $90.8\%$ 。

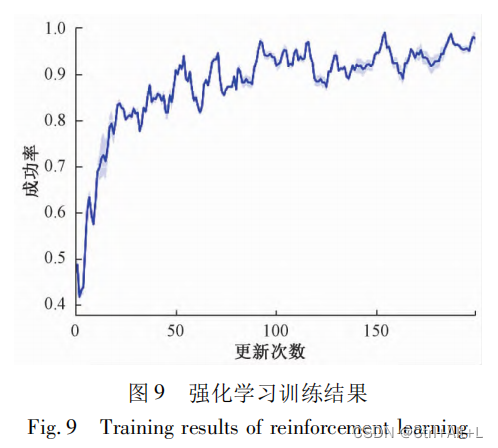
4.2 HP 算法的仿人性验证

通过对比第 1. 1 节中机械臂各关节的仿人运动范围能够发现，在对上述目标点进行达点运动时，机械臂各关节的运动范围均满足仿人运动范围的要求，不存在超过人体手臂运动范围的运动。

根据机械臂的上述各项运动指标，即运动轨迹和关节角变化范围，能够初步判定，通过 HP 算法规划的运动具备仿人性的特征。

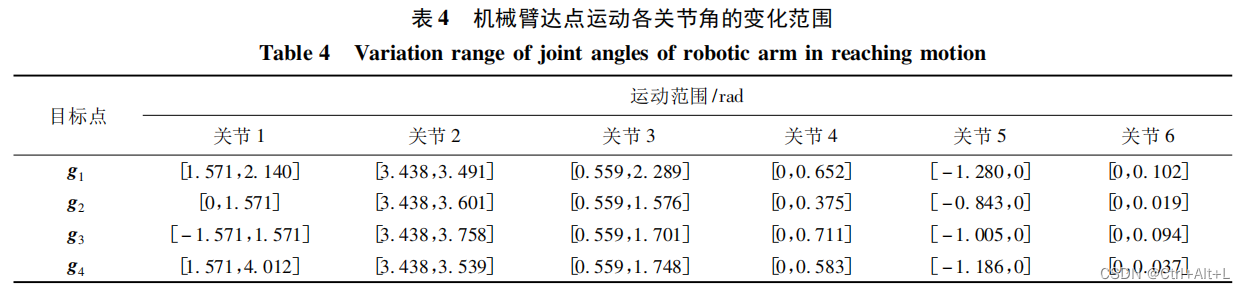
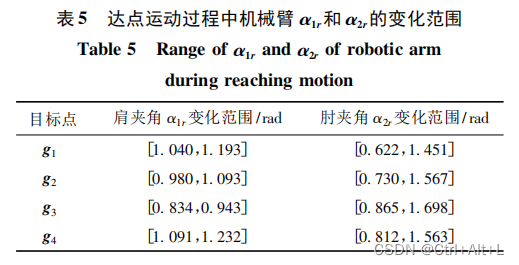
4.3 机械臂仿人运动结果分析

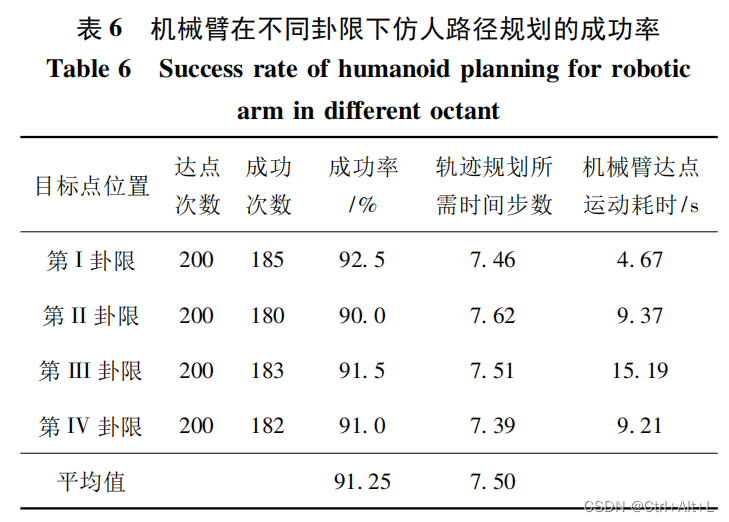
机械臂在每个卦限下的达点运动都具备仿人性
每一卦限下的成功率和仿人轨迹规划耗时的差距并不大

5 结论