- 1java输出的时候出现[Ljava.lang.String是什么意思+解决方法
- 2机器学习中的Encoder和Decoder到底是什么
- 3华为OD机试 - 文件缓存系统(Java & JS & Python & C++)_华为od文件缓存系统
- 4C++ 命名空间(Namespace)
- 5【VScode】Remote-SSH XHR failed无法访问远程服务器_vscode ssh xhr failed
- 6《深度学习入门之PyTorch》书籍阅读笔记
- 7手把手教你使用ChatGPT辅助写论文_利用chatgpt 写文章
- 8Golang开发环境搭建-Vim篇_干净的开发环境 vim
- 9php pdf只能查看不能下载,对于pdf文件不支持浏览器下载如何处理?
- 10各种算法的理论总结_算法理论
各种注意力机制的PyTorch实现_注意力机制代码
赞
踩
一、符号说明
采用和PyTorch官方文档相似的记号:
| 符号 | 描述 |
|---|---|
| d q d_q dq | 查询向量的维度 |
| d k d_k dk | 键向量的维度 |
| d v d_v dv | 值向量的维度 |
| n n n | 查询的个数 |
| m m m | 键-值对的个数 |
| N N N | 批量大小 |
| L L L | 序列长度 |
导入本文所需要的包
import math
import torch
import torch.nn as nn
import torch.nn.functional as F
- 1
- 2
- 3
- 4
二、注意力评分函数
设有查询 q q q 和 m m m 个键-值对 { ( k i , v i ) } i = 1 m \{(k_i,v_i)\}_{i=1}^m {(ki,vi)}i=1m,接下来我们会计算每一个 a ( q , k i ) a(q,k_i) a(q,ki),其中 a ( ⋅ , ⋅ ) a(\cdot,\cdot) a(⋅,⋅) 是注意力评分函数,然后将其扔到softmax里得到 m m m 个注意力权重 α ( q , k i ) \alpha(q,k_i) α(q,ki),于是注意力机制的输出是一个向量:
Attn ( q , { ( k i , v i ) } i = 1 m ) = ∑ i = 1 m α ( q , k i ) v i = ∑ i = 1 m softmax ( a ( q , k i ) ) v i \text{Attn}(q,\{(k_i,v_i)\}_{i=1}^m)=\sum_{i=1}^m\alpha(q,k_i)v_i=\sum_{i=1}^m\text{softmax}(a(q,k_i))v_i Attn(q,{(ki,vi)}i=1m)=i=1∑mα(q,ki)vi=i=1∑msoftmax(a(q,ki))vi
通常来讲, m m m 个键-值对是固定的,但查询 q q q 可能不止一个,有多少个查询注意力机制就会输出多少个向量,即:
Attn ( { q i } i = 1 n , { ( k j , v j ) } j = 1 m ) = { ∑ j = 1 m softmax ( a ( q i , k j ) ) v j } i = 1 n \text{Attn}(\{q_i\}_{i=1}^n,\{(k_j,v_j)\}_{j=1}^m)=\left\{\sum_{j=1}^m\text{softmax}(a(q_i,k_j))v_j\right\}_{i=1}^n Attn({qi}i=1n,{(kj,vj)}j=1m)={j=1∑msoftmax(a(qi,kj))vj}i=1n
下图形象地展示了注意力汇聚的过程
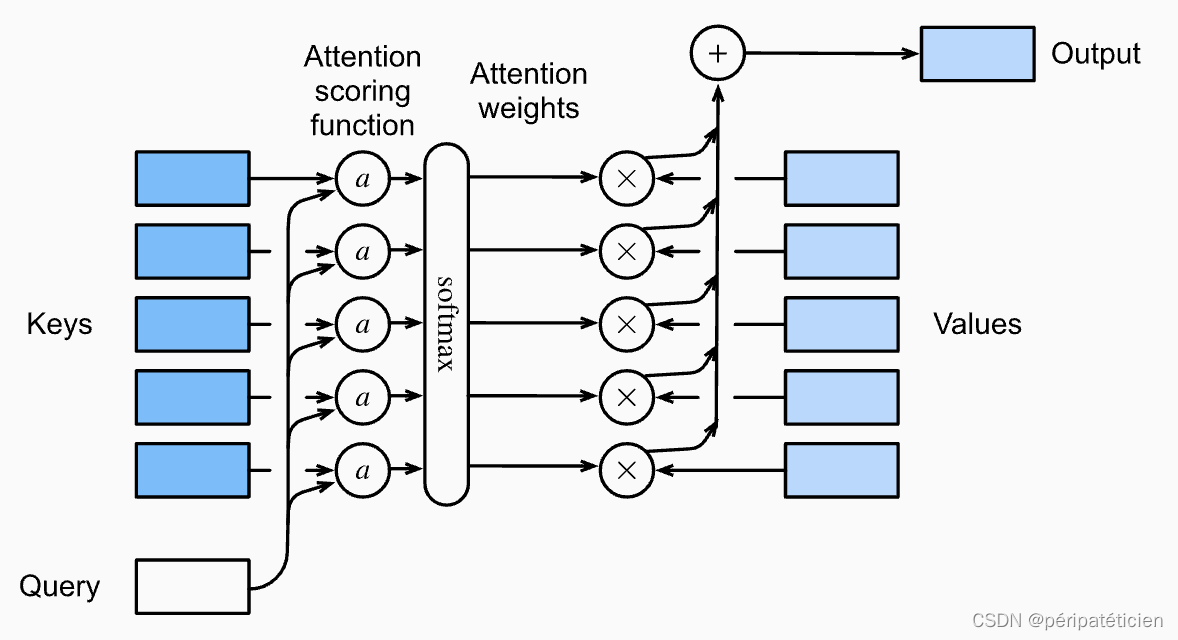
2.1 加性注意力
当 d q ≠ d k d_q\neq d_k dq=dk 时,通常使用加性注意力
a ( Q , K ) = tanh ( Q W q + K W k ) W v T a(Q,K)=\tanh(QW_q+KW_k)W_v^{\mathrm T} a(Q,K)=tanh(QWq+KWk)WvT
其中 Q , K , W v , W q , W k Q,K,W_v,W_q,W_k Q,K,Wv,Wq,Wk 的形状分别为 ( n , d q ) , ( m , d k ) , ( 1 , h ) , ( d q , h ) , ( d k , h ) (n,d_q),(m,d_k),(1,h),(d_q,h),(d_k,h) (n,dq),(m,dk),(1,h),(dq,h),(dk,h)。
因为
Q
W
q
QW_q
QWq 和
K
W
k
KW_k
KWk 的形状分别为
(
n
,
h
)
(n,h)
(n,h) 和
(
m
,
h
)
(m,h)
(m,h),不能直接相加,所以需要先将其形状分别扩展为
(
n
,
1
,
h
)
(n,1,h)
(n,1,h) 和
(
1
,
m
,
h
)
(1,m,h)
(1,m,h),然后再进行广播相加,得到形状为
(
n
,
m
,
h
)
(n,m,h)
(n,m,h) 的张量。乘上
W
v
T
W_v^{\mathrm T}
WvT 后,需要做一个 squeeze 操作,因此
a
(
Q
,
K
)
a(Q,K)
a(Q,K) 的形状为
(
n
,
m
)
(n,m)
(n,m)。
于是可得注意力汇聚函数为
Attn ( Q , K , V ) = softmax ( tanh ( Q W q + K W k ) W v T ) V \text{Attn}(Q,K,V)=\text{softmax}(\tanh(QW_q+KW_k)W_v^{\mathrm T})V Attn(Q,K,V)=softmax(tanh(QWq+KWk)WvT)V
其中 softmax \text{softmax} softmax 操作在 a ( Q , K ) a(Q,K) a(Q,K) 的最后一个维度上进行, V V V 的形状为 ( m , d v ) (m,d_v) (m,dv),最终得到的 Attn ( Q , K , V ) \text{Attn}(Q,K,V) Attn(Q,K,V) 的形状为 ( n , d v ) (n,d_v) (n,dv)。
PyTorch实现如下:
class AdditiveAttention(nn.Module):
def __init__(self, query_size, key_size, hidden_size):
super().__init__()
self.W_q = nn.Linear(query_size, hidden_size, bias=False)
self.W_k = nn.Linear(key_size, hidden_size, bias=False)
self.W_v = nn.Linear(hidden_size, 1, bias=False)
def forward(self, query, key, value):
"""
Args:
query: (N, n, d_q)
key: (N, m, d_k)
value: (N, m, d_v)
"""
query, key = self.W_q(query).unsqueeze(2), self.W_k(key).unsqueeze(1)
attn_weights = F.softmax(self.W_v(torch.tanh(query + key)).squeeze(), dim=-1) # (N, n, m)
return attn_weights @ value # (N, n, d_v)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
这里的 @ 相当于 torch.bmm。
2.2 缩放点积注意力
当 d q = d k ≜ d d_q= d_k\triangleq d dq=dk≜d 时,通常使用缩放点积注意力
a ( Q , K ) = Q K T d a(Q,K)=\frac{QK^{\mathrm T}}{\sqrt{d}} a(Q,K)=d QKT
其中 Q , K Q,K Q,K 的形状分别为 ( n , d ) , ( m , d ) (n,d),(m,d) (n,d),(m,d), a ( Q , K ) a(Q,K) a(Q,K) 的形状为 ( n , m ) (n,m) (n,m)。
于是可得注意力汇聚函数为
Attn ( Q , K , V ) = softmax ( Q K T d ) V \text{Attn}(Q,K,V)=\text{softmax}\Big(\frac{QK^{\mathrm T}}{\sqrt{d}}\Big)V Attn(Q,K,V)=softmax(d QKT)V
其中 softmax \text{softmax} softmax 操作在 a ( Q , K ) a(Q,K) a(Q,K) 的最后一个维度上进行, V V V 的形状为 ( m , d v ) (m,d_v) (m,dv),最终得到的 Attn ( Q , K , V ) \text{Attn}(Q,K,V) Attn(Q,K,V) 的形状为 ( n , d v ) (n,d_v) (n,dv)。
PyTorch实现如下:
class ScaledDotProductAttention(nn.Module):
def __init__(self):
super().__init__()
def forward(self, query, key, value):
"""
Args:
query: (N, n, d)
key: (N, m, d)
value: (N, m, d_v)
"""
return F.softmax(query @ key.transpose(1, 2) / math.sqrt(query.size(2)), dim=-1) @ value
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
2.3 mask与dropout
先前我们实现的注意力评分函数为了简便起见没有引入掩码机制,一般而言我们会在注意力机制中加入mask和dropout,对于前者,具体会用到 masked_fill 方法,例如
a = torch.randn(4, 4)
print(a)
# tensor([[ 0.9105, 0.1080, -0.2465, 1.8417],
# [ 0.2210, 0.3447, -2.0660, 0.7162],
# [-0.0277, -0.0303, -0.4582, -0.6497],
# [-0.1733, 0.9065, 0.5338, 1.0596]])
mask = torch.tensor([
[False, False, False, True],
[False, False, True, True],
[False, True, True, True],
[True, True, True, True]
]) # mask不一定要与a的形状相同,只要能广播成a的形状即可
b = a.masked_fill(mask, 0)
print(b)
# tensor([[ 0.9105, 0.1080, -0.2465, 0.0000],
# [ 0.2210, 0.3447, 0.0000, 0.0000],
# [-0.0277, 0.0000, 0.0000, 0.0000],
# [ 0.0000, 0.0000, 0.0000, 0.0000]])
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
对于后者,仅需调用 nn.Dropout 即可。
在引入mask和dropout后,两种注意力评分函数变为
class AdditiveAttention(nn.Module):
def __init__(self, query_size, key_size, hidden_size, drouput=0):
super().__init__()
self.W_q = nn.Linear(query_size, hidden_size, bias=False)
self.W_k = nn.Linear(key_size, hidden_size, bias=False)
self.W_v = nn.Linear(hidden_size, 1, bias=False)
self.dropout = nn.Dropout(drouput)
def forward(self, query, key, value, attn_mask=None):
"""
Args:
query: (N, n, d_q)
key: (N, m, d_k)
value: (N, m, d_v)
attn_mask: (N, n, m)
"""
query, key = self.W_q(query).unsqueeze(2), self.W_k(key).unsqueeze(1)
scores = self.W_v(torch.tanh(query + key)).squeeze() # (N, n, m)
if attn_mask is not None:
scores = scores.masked_fill(attn_mask, float('-inf')) # 经过softmax后负无穷的地方会变成0
attn_weights = F.softmax(scores, dim=-1) # (N, n, m)
return self.dropout(attn_weights) @ value # (N, n, d_v)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
class ScaledDotProductAttention(nn.Module):
def __init__(self, dropout=0):
super().__init__()
self.dropout = nn.Dropout(dropout)
def forward(self, query, key, value, attn_mask=None):
"""
Args:
query: (N, n, d_k)
key: (N, m, d_k)
value: (N, m, d_v)
attn_mask: (N, n, m)
"""
assert query.size(2) == key.size(2)
scores = query @ key.transpose(1, 2) / math.sqrt(query.size(2))
if attn_mask is not None:
scores = scores.masked_fill(attn_mask, float('-inf'))
attn_weights = F.softmax(scores, dim=-1)
return self.dropout(attn_weights) @ value
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/小丑西瓜9/article/detail/347921
Copyright © 2003-2013 www.wpsshop.cn 版权所有,并保留所有权利。


