自适应滤波器原理——最小均方算法（LMS）_lms算法原理

1959年由Widrow和Hoff提出了最小均方（Least Mean Square，LMS）算法，LMS基于维纳滤波理论，采用瞬时值估计梯度矢量的算法，通过最小化误差信号的能量来更新自适应滤波器权值系数。

设计一个N 阶滤波器，它的参数为w(n)，则滤波器输出为

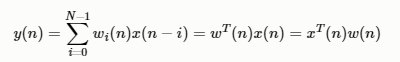
 期望输出为d(n)，则误差信号可以定义为：

我们的目标就是将误差e(n)最小化，采用最小均方误差（MMSE ）准则，最小化目标函数：J(w)

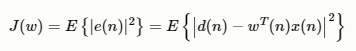
计算目标函数J(w)对w的导数，令导数为0：

 

 则滤波器系数的更新公式可以写为：

 上式中的μ为步长因子。μ值越大，算法收敛越快，但稳态误差也越大；μ值越小，算法收敛越慢，但稳态误差也越小。为保证算法稳态收敛，应使μ在以下范围取值：

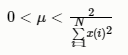
• 优点：算法简单，易于实现，算法复杂度低(LMS<RLS)，能够抑制旁瓣效应
• 缺点：
  • 收敛速率较慢(LMS<RLS)，因为LMS滤波器系数更新是逐点的（每来一个新的x(n)和d(n)，滤波器系数就更新一次）,每一次采样点梯度的估计对于真实梯度会存在误差，导致滤波器系数的每次更新不会严格按照真实梯度方向更新，而是有一定的偏差
  • 跟踪性能较差，并且随着滤波器阶数(步长参数)升高，系统的稳定性下降
  • LMS要求不同时刻的输入向量x(n)线性无关——LMS 的独立性假设。如果输入信号存在相关性，会导致前一次迭代产生的梯度噪声传播到下一次迭代，造成误差的反复传播，收敛速度变慢，跟踪性能变差。

所以，理论上，LMS 算法对白噪声的效果最好。为了降低输入信号的相关性，出现了一类“解相关LMS”算法。

在现实场景中，常常会遇到以下两种情况：

一、我们往往是无法事先得到期望信号（干净信号），假如我们已经得到了干净信号了，那么我们干嘛还要滤波呢。因此，在仅知道带噪信号:这种情况下，带噪信号作为参考信号，然后对带噪信号进行延迟处理，延迟的信号作为输入信号。这样做的目的是假定在延迟的时间段内，信号仍是相关的，但噪声却不相关。通过去相关来去除噪声分量，一次延迟的时间需要设置合理，如自适应线谱增强器（ALE）。

二、我们已知带噪信号和噪声，可以把带噪信号作为输入信号，噪声为参考信号。

MATLAB代码如下：

function [e, y, w] = myLMS(d, x, mu, M)
% Inputs:
% d  - 麦克风语音
% x  - 远端语音
% mu - 步长，0.05
% M  - 滤波器阶数，也称为抽头数
%
% Outputs:
% e - 输出误差，近端语音估计
% y  - 输出系数，远端回声估计
% w - 滤波器参数
 
    d_length = length(d);
    if (d_length <= M)  
        print('error: 信号长度小于滤波器阶数！');
        return; 
    end
    if (d_length ~= length(x))  
        print('error: 输入信号和参考信号长度不同！');
        return; 
    end
 
    xx = zeros(M,1);
    w1 = zeros(M,1);    % 滤波器权重
    y = zeros(d_length,1);  % 远端回声估计
    e = zeros(d_length,1);  % 近端语音估计
 
    % for n = 1:Ns
    %     xx = [xx(2:M);x(n)];    % 纵向拼接
    %     xx(2~40)+x(1)-->xx(2~40)+x(2)-->xx(2~40)+x(3)...
    %     y(n) = w1' * xx;        % 远端回声估计(40,1)'*(40,1)=1; (73113,1)
    %     e(n) = d(n) - y(n);     % 近端语音估计
    %     w1 = w1 + mu * e(n) * xx;   % (40,1)
    %     w(:,n) = w1;        % (40, 73113)
    % end
    % 和上面类似
    for n = M:d_length
        xx = x(n:-1:n-M+1);    % 纵向拼接  (40~1)-->(41~2)-->(42~3)....
        y(n) = w1' * xx;        % 远端回声估计 (40,1)'*(40,1)=1; (73113,1)
        e(n) = d(n) - y(n);     % 近端语音估计
        w1 = w1 + mu * e(n) * xx;   % (40,1)
        w(:,n) = w1;        % (40, 73113)
    end
end

参考链接：

https://www.cnblogs.com/LXP-Never/p/11773190.html