热门标签
当前位置: article > 正文
[Algorithm][动态规划][01背包问题][目标和][最后一块石头的重量Ⅱ]详细讲解
作者:从前慢现在也慢 | 2024-07-05 02:33:16
赞
踩
[Algorithm][动态规划][01背包问题][目标和][最后一块石头的重量Ⅱ]详细讲解
1.目标和
1.题目链接
2.算法原理详解
-
问题转化:在数组中选择一些数,让这些数的和等于
a,一共有多少种选法?–> 01背包
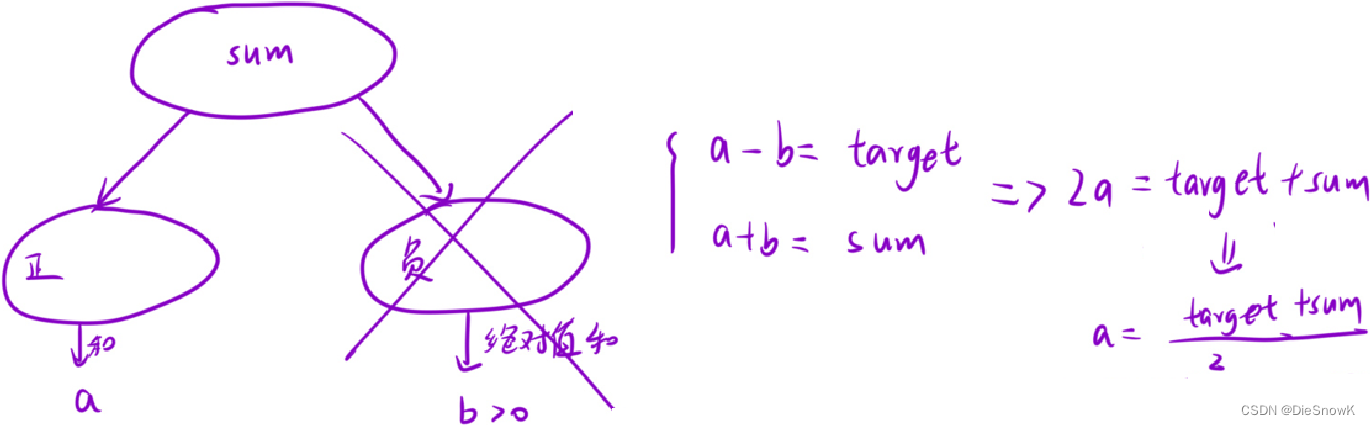
-
思路:
-
确定状态表示 ->
dp[i][j]的含义dp[i]j]:从前i个数中**选**,总和正好等于j,一共有多少种选法
-
推导状态转移方程:根据最后一个位置的情况,分情况讨论
dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]]

-
初始化:
- 多开一行及一列虚拟结点
- 第一列除
[0, 0],其余无需初始化- 这里第一列不会越界访问,可以交给DP阶段处理
- 因为只有
dp[i - 1][j - nums[i]]可能越界访问- 但是在判定后,只有
j == nums[i] == 0的情况,才会进入第一列,此时又不会越界 - 如果不符合条件,就不会进来,也不会触发越界访问

- 但是在判定后,只有
-
确定填表顺序:从上往下
-
确定返回值:
dp[n][a]
-
-
滚动数字优化同[模板] 背包
3.代码实现
// v1.0 int findTargetSumWays(vector<int>& nums, int target) { // 问题转换 int sum = 0; for(auto& x : nums) { sum += x; } int aim = (sum + target) / 2; // 边界处理 if(aim < 0 || (sum + target) % 2) return 0; int n = nums.size(); vector<vector<int>> dp(n + 1, vector<int>(aim + 1)); dp[0][0] = 1; for(int i = 1; i <= n; i++) { for(int j = 0; j <= aim; j++) // 第一列没有初始化,也在DP阶段处理 { dp[i][j] = dp[i - 1][j]; if(j >= nums[i - 1]) { dp[i][j] += dp[i - 1][j - nums[i - 1]]; } } } return dp[n][aim]; } ----------------------------------------------------------------------- // v2.0 滚动数组优化 int findTargetSumWays(vector<int>& nums, int target) { // 问题转换 int sum = 0; for(auto& x : nums) { sum += x; } int aim = (sum + target) / 2; // 边界处理 if(aim < 0 || (sum + target) % 2) return 0; int n = nums.size(); vector<int> dp(aim + 1); dp[0] = 1; for(int i = 1; i <= n; i++) { for(int j = aim; j >= nums[i - 1]; j--) { dp[j] += dp[j - nums[i - 1]]; } } return dp[aim]; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
2.最后一块石头的重量 II
1.题目链接
2.算法原理详解
-
问题转化:在数组中选择一些数,让这些数的和尽可能接近
sum / 2- 问题转化成了目标和–> 01背包
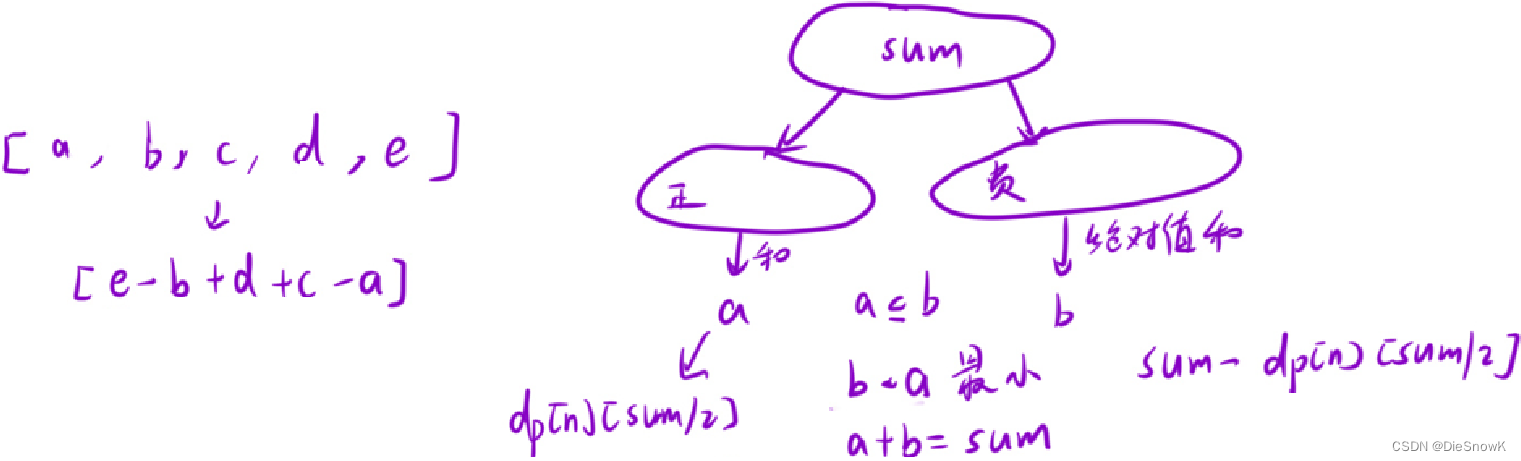
- 问题转化成了目标和–> 01背包
-
思路:
-
确定状态表示 ->
dp[i][j]的含义dp[i]j]:从前i个数中**选**,总和不超过j,此时的最大和
-
推导状态转移方程:根据最后一个位置的情况,分情况讨论
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - nums[i]] + nums[i])
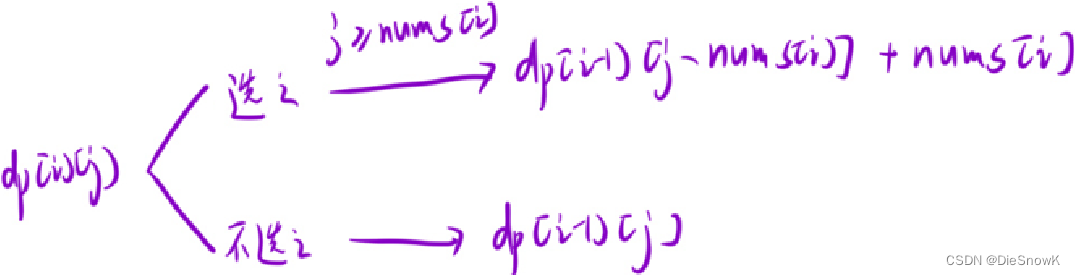
-
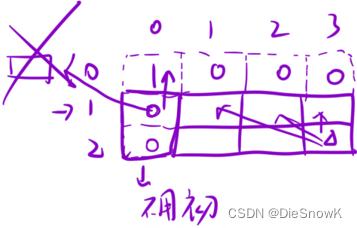
初始化:
- 多开一行及一列虚拟结点
- 第一列除
[0, 0],其余无需初始化- 这里第一列不会越界访问,可以交给DP阶段处理
- 因为只有
dp[i - 1][j - stones[i - 1]]可能越界访问- 但是在判定后,只有
j == stones[i - 1] == 0的情况,才会进入第一列,此时又不会越界 - 如果不符合条件,就不会进来,也不会触发越界访问
- 但是在判定后,只有
-
确定填表顺序:从上往下
-
确定返回值:
sum - 2 * dp[n][sum / 2]
-
-
滚动数字优化同[模板] 背包
3.代码实现
// v1.0 int lastStoneWeightII(vector<int>& stones) { int sum = 0; for(auto& x : stones) { sum += x; } int n = stones.size(), m = sum / 2; vector<vector<int>> dp(n + 1, vector<int>(m + 1)); for(int i = 1; i <= n; i++) { for(int j = 0; j <= m; j++) { dp[i][j] = dp[i - 1][j]; if(j >= stones[i - 1]) { dp[i][j] = max(dp[i][j], dp[i - 1][j - stones[i - 1]] + stones[i - 1]); } } } return sum - 2 * dp[n][m]; } ----------------------------------------------------------------------- // v2.0 滚动数组优化 int lastStoneWeightII(vector<int>& stones) { int sum = 0; for(auto& x : stones) { sum += x; } int n = stones.size(), m = sum / 2; vector<int> dp(m + 1); for(int i = 1; i <= n; i++) { for(int j = m; j >= stones[i - 1]; j--) { dp[j] = max(dp[j], dp[j - stones[i - 1]] + stones[i - 1]); } } return sum - 2 * dp[m]; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/从前慢现在也慢/article/detail/788927
推荐阅读
相关标签



