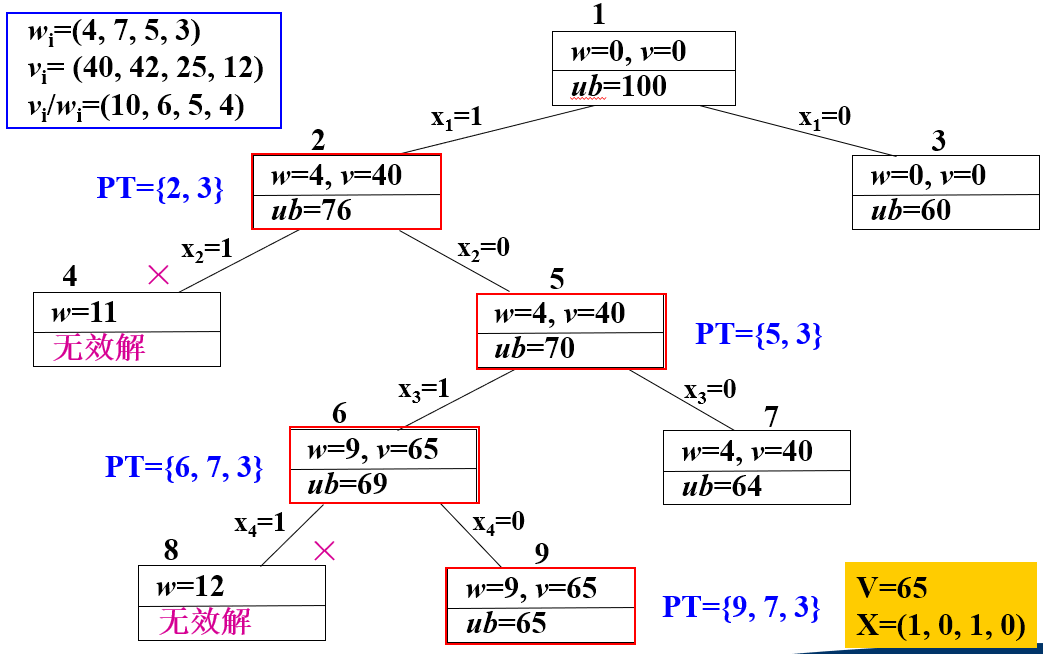
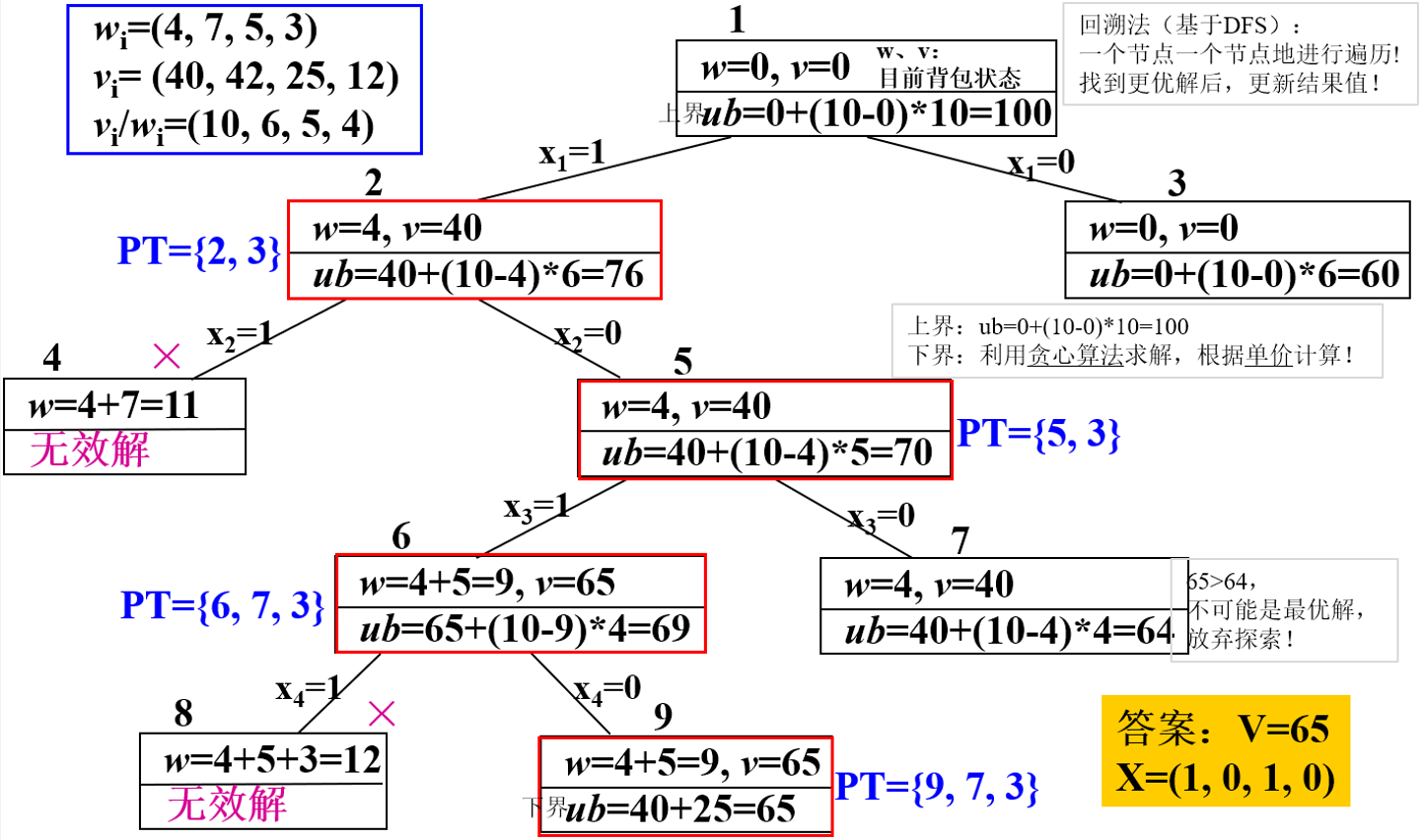
分支界限算法【0-1背包问题】按照优先队列式（LC）分支限界法求解0-1背包问题， 并给出限界函数，并画出该实例的状态空间树。_0/1背包问题的lc分支限界法状态空间树

目   录

回溯算法【0-1背包问题】

分支界限算法【0-1背包问题】

作业题（期末考试必考）

小结

---

回溯算法【0-1背包问题】

分支界限算法【0-1背包问题】

解决思路：采用优先队列式分支限界

Ø 确定 目标函数上、下界；

Ø 确定 目标函数的计算方法；

一般情况下，假设当前已对前i个物品进行了某种特定的选择，且背包中已装入物品的重量是w，获得的价值是v，计算该结点的目标函数上界的一个简单方法是，将背包中剩余容量全部装入第i+1个物品，并可以将背包装满，于是，得到限界函数：

Ø 依 上计算从 根结点到叶子结点的目标函数值 直到 表 PT （待处理活结点列表）中 取得极大值 。

分支限界法求解0/1背包问题算法用伪代码描述如下：

算法7.1：分枝限界法求解0/1背包问题

输入：n个物品的重量w[n]，价值v[n]，背包容量W

输出：背包获得的最大价值和装入背包的物品

1. 根据限界函数计算目标函数的上界up；采用贪心法得到下界down；

2. 计算根结点的目标函数值并加入待处理结点表PT；

3. 循环直到某个叶子结点的目标函数值在表PT中取极大值

   3.1  i = 表PT中具有最大值的结点；

   3.2 对结点i的每个孩子结点x执行下列操作：

         3.2.1 如果结点x不满足约束条件，则丢弃该结点；

         3.2.2 否则，估算结点x的目标函数值lb，

                  将结点x加入表PT中；

4. 将叶子结点对应的最优值输出，回溯求得最优解的各个分量。

作业题（期末考试必考）

按照优先队列式（LC）分支限界法求解0-1背包问题， 并给出限界函数，并画出该实例的状态空间树。

老师讲解此题的板书：

博主课堂笔记（仅供参考）：

背包容量下界的计算：

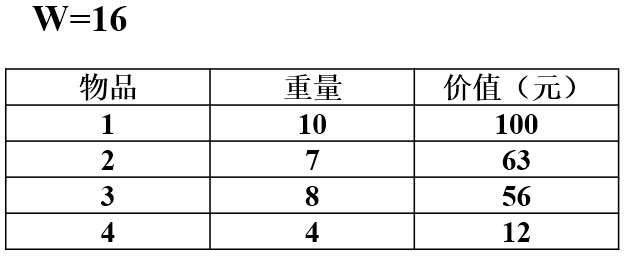
背包容量W=16。
①放入物品1(w1=10;v1=100)和物品4(w4=4;v4=12)，背包物品总重量w=14，v=112；
②放入物品2(w1=  7;v1=63  )和物品4(w4=4;v4=12)，背包物品总重量w=11，v= 75；
③放入物品3(w1=  8;v1=56  )和物品4(w4=4;v4=12)，背包物品总重量w=12，v= 68。
下界取最大值，即下界w=112。

小结

回溯算法和分支限界算法在最坏情况下需要遍历所有的节点，因此其最坏的算法时间效率也是指数级的。