5. ＜tag-数组模拟矩阵＞-lt.48- 旋转图像(全部解法) + lt.59-螺旋矩阵 II 1.5_tag矩阵

lt. 48 旋转图像 (同面试题 01.07. 旋转矩阵)

[案例需求]

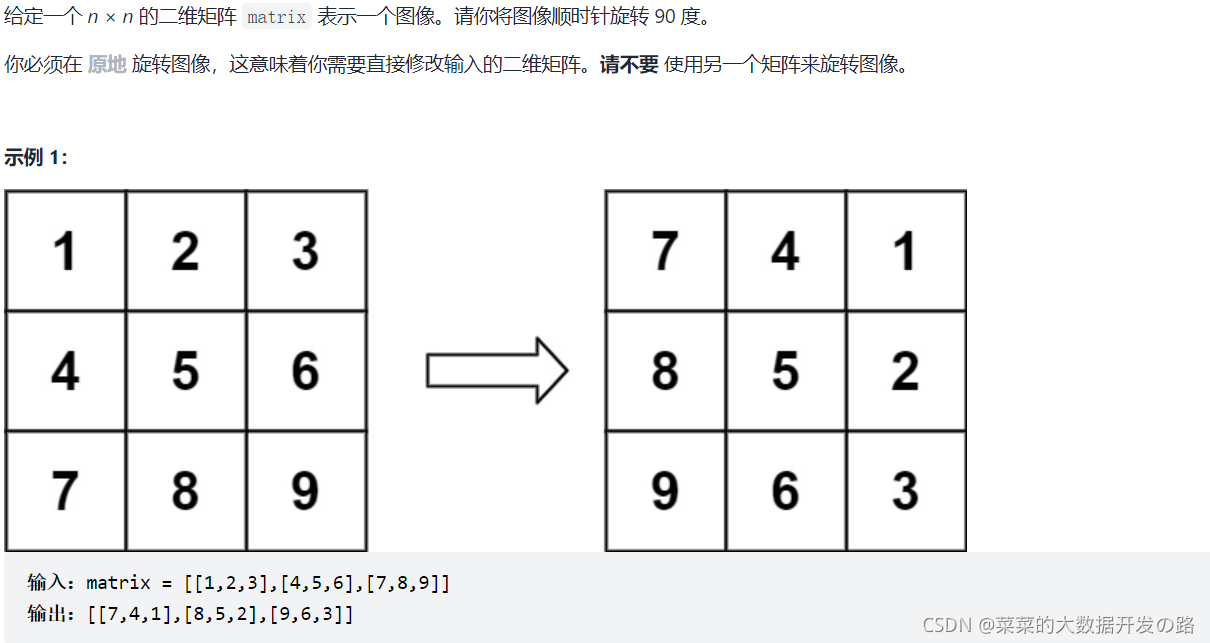
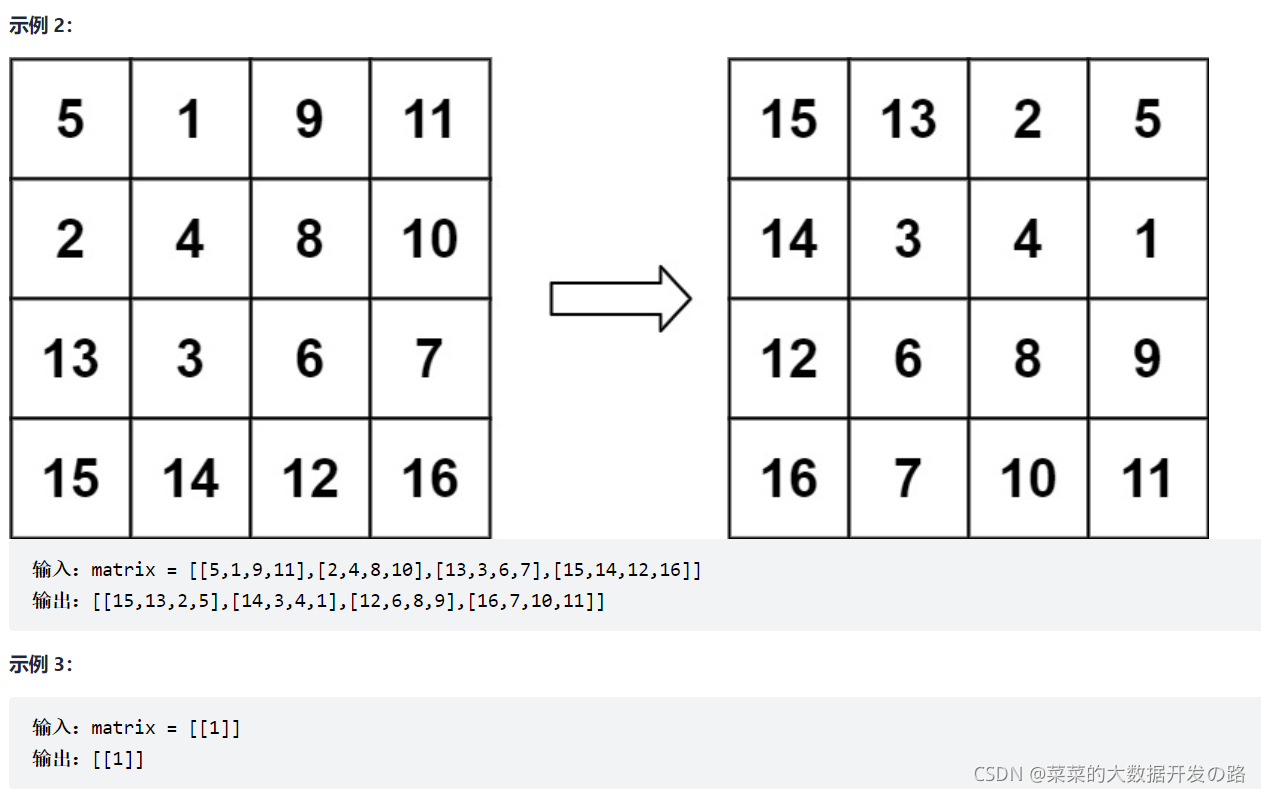
[思路一, 转置+翻转, 时间复杂度 N<sup>2</sup>, 空间复杂度 1]

1. 没啥可说的, 对于旋转图像即旋转矩阵的问题, 我们首先考虑数学解法, 本题可以得出: 为了90°旋转矩阵, 我们可以先对矩阵转置, 再把转置后的矩阵进行翻转 (我们也可以进行列交换, (第一列和最后一列, 第二列和倒数第二列交换…))

[代码实现]

class Solution {
    public void rotate(int[][] matrix) { 
	// 二维数组模拟矩阵, 对矩阵进行转置;
		for(int i = 0; i < matrix.length; i++){
		//为什么j=i?  因为每一次转置都会有一列元素转置完成, 而j控制列, 
        //每一次行往下遍历时, j都要增大 一次, 把j设置为i正好符合这种需求
			for(int j = i; j < matrix[i].length; j++){
						int temp  = matrix[i][j];
                        matrix[i][j] = matrix[j][i];
                        matrix[j][i] = temp;
			}
        }
            //转置完成后, 对每一行进行反转
            for(int i = 0; i < matrix.length; i++){

                int start = 0;
                int end = matrix[i].length - 1;
                
                while(start < end){
                
                    int temp1 = matrix[i][start];
                    matrix[i][start] = matrix[i][end];
                    matrix[i][end] = temp1;

                    start++;
                    end--;
                }   
            }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

[思路二, 找规律, 时间复杂度 N<sup>2</sup>, 空间复杂度 1]

lt. 59 旋转矩阵 II

[案例需求]

[思路分析]

• //其实跟螺旋数组I的思路基本一致, 只不过之前是遍历螺旋矩阵, 这次是写入螺旋矩阵,
• //所以我们可以模仿前面螺旋矩阵的遍历方式,并同时插入规定的数 1–>n*n

[代码实现]

class Solution {
    public int[][] generateMatrix(int n) {
       

        //指定四个角(数组的索引)
        int left = 0;
        int right = n -1;
        int top = 0;
        int bottom = n - 1;

        // n*n的最大数以及得到的结果数组
        int maxNum = n * n;
        int[][] res = new int[n][n];
        int index = 0; //数组的索引
        int num = 1; //起始的写入数组数

        //遍历
        //老样子, left和right控制列. top和bottom控制行
        while(left < right && top < bottom){
            //由左到右遍历,不是, 是写入
            for(int i = left; i < right; i++){
                res[top][i] = num++;
            }

            //由上到下写入
            for(int i = top; i < bottom; i++){
                res[i][right] = num++;
            }

            //由右向左写入
            for(int i = right; i > left; i--){
                res[bottom][i] = num++;
            }

            //由下向上写入
            for(int i = bottom; i > top; i--){
                res[i][left] = num++;
            }

            ++left;
            --right;
            ++top;
            --bottom;
        }

        // 当只剩最后一列,或者最后一行数据,或最后一个数字需要写到martix中
        if(left == right){
            for(int i = top; i <=bottom; i++){res[i][left] = num++;}
        }else if(top == bottom){
            for(int i = left; i <= right; i++){res[top][i] = num++;}
        }

        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55