回溯法-01背包问题之一：递归模式_01背包递归

一、回溯法

回溯法是一个既带有系统性又带有跳跃性的搜索算法。它在包含问题的所有解的解空间树中按照深度优先的策略，从根节点出发搜索解空间树。算法搜索至解空间树的任一节点时，总是先判断该节点是否肯定不包含问题的解。如果肯定不包含，则跳过对以该节点为根的子树的系统搜索，逐层向其原先节点回溯。否则，进入该子树，继续按深度优先的策略进行搜索。

运用回溯法解题通常包含以下三个步骤：

· 针对所给问题，定义问题的解空间；

· 确定易于搜索的解空间结构；

· 以深度优先的方式搜索解空间，并且在搜索过程中用剪枝函数避免无效搜索；

二、01背包问题描述

01背包问题，即向容量为M的背包装载物品，要么放入要么不放入。从n个物品中选取装入背包的物品，物品i的重量为Wi，价值为Pi。最佳装载指装入的物品价值最高，即∑PiXi(i=1..n)取最大值。约束条件为∑WiXi≤M且Xi∈[0,1](1≤i≤n)。

在这个表达式中，需求出Xi的值。Xi=1表示物品i装入背包，Xi＝0表示物品i不装入背包。

· 即判断可行解的约束条件是：∑WiXi≤M（i=0..n），Wi>0,Xi∈[0,1](1≤i≤n)

· 目标最大值：max∑PiXi（i=0..n-1）,Pi>0,Xi=0或1（0≤i<n）

0/1背包问题是一个自己选取问题，适合于用子集树表示0／1背包问题的解空间。在搜索解空间树时，只要左儿子节点是一个可行节点，搜索就进入左子树，在右子树中有可能包含最优解才进入右子树搜索，否则将右子树剪去。

三、关于剪枝函数

设当前剩余物品价值总和为r，当前结点x价值为cp，当前x结点上界函数值为bp。L为当前已搜索到的答案结点中受益的最大值，当cp+r=bp<L时可剪去以X为根的子树。

计算右子树中解上界方法是将剩余物品按单位重量价值排序，一次放入物品直至装不下为止，再装入部分未装入物品直至装满背包，由此得到的价值是右子树解上界。

四、递归实现

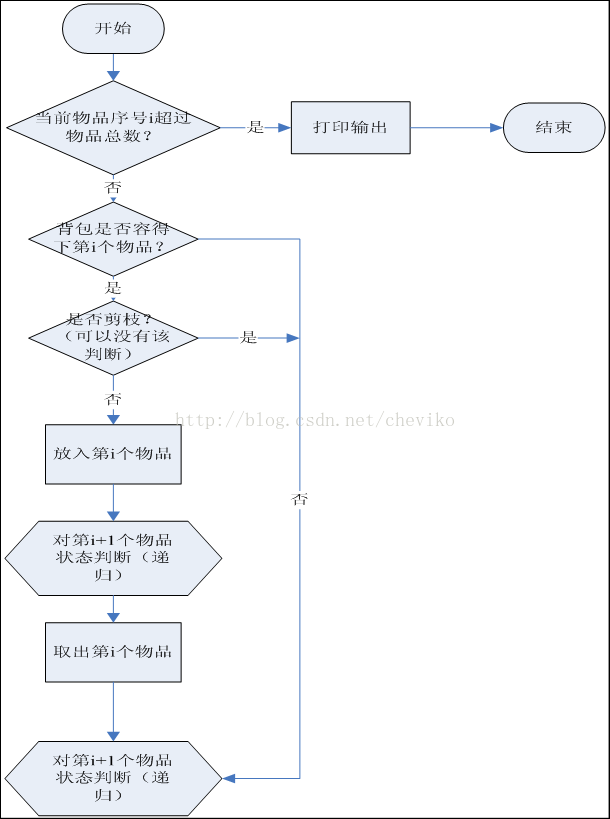
如下图1所示为01背包问题递归实现的示意图，图2是01背包问题递归实现的流程图，描述了代码实现方案。

                                 

图1 01背包问题递归描述图                                     图2 01背包问题递归实现流程图

图1比较容易理解，是否已拿完物品也就是i<n(i是当前物品序号，n是物品总数目)是否成立，如果成立则递归结束并打印输出路径。如果i<n则判断第i个物品能否放入背包，如果不能放入，则考虑放置i+1个物品，如果能放入还存在当前第i个放入和不放入两种情形后对第i+1个的影响。注意在“放入还是不放入”的部分可考虑加入剪枝函数。

五、递归的代码实现

代码1 Main函数测试代码：

public static void Main (string[] args)
		{
            Obj[] objs = new Obj[4];
            objs[0] = new Obj() { Weight = 7, Price = 42 };
            objs[1] = new Obj() { Weight = 3, Price = 12 };
            objs[2] = new Obj() { Weight = 4, Price = 40 };
            objs[3] = new Obj() { Weight = 5, Price = 25 };
 
            Backtracking_Recursion1 r = new Backtracking_Recursion1();
            r.W = 10;
            r.objs = objs;
            r.Backtracking(0);
 
            Console.Read();
		}

代码2Obj物品代码

public class Obj
    {
        /// <summary>
        /// 物品重量
        /// </summary>
        public int Weight
        {
            get;
            set;
        }
        /// <summary>
        /// 物品价值
        /// </summary>
        public int Price
        {
            get;
            set;
        }
        /// <summary>
        /// 该物品是否放入包内
        /// </summary>
        internal bool Selected
        {
            get;
            set;
        }
    }

代码3递归实现01背包问题

class Backtracking_Recursion1
    {
        #region field
        protected int m_currentWeight = 0;
        protected int m_currentPrice = 0;
        #endregion
        #region property
        /// <summary>
        /// 背包容量
        /// </summary>
        /// <value>默认20</value>
        public int W
        {
            get;
            set;
        }
 
        public int n
        {
            get
            {
                return objs == null ? 0 : objs.Length;
            }
        }
 
        /// <summary>
        /// 物品，包括重量／价值和数量
        /// </summary>
        /// <value>The objects.</value>
        public Obj[] objs
        {
            get;
            set;
        }
        #endregion
        public void Backtracking(int i)
        {
            if (i >= n)
            {
                Printing();
                return;
            }
 
            if (objs[i].Weight + m_currentWeight <= W)
            {
                m_currentWeight += objs[i].Weight;
                m_currentPrice += objs[i].Price;
                objs[i].Selected = true;
 
                Backtracking(i + 1);
 
                m_currentPrice -= objs[i].Price;
                m_currentWeight -= objs[i].Weight;
            }
            objs[i].Selected = false;
            Backtracking(i + 1);
        }
 
        /// <summary>
        /// 输出路径
        /// </summary>
        protected void Printing()
        {
            Console.Write("<");
            for (int i = 0; i < objs.Length; i++)
            {
                Console.Write(objs[i].Selected ? "1 " : "0 ");
 
            }
            Console.WriteLine(">, price: " + m_currentPrice.ToString()
                               + "\t weight: " + m_currentWeight.ToString());
        }
    }

六运行结果

注：

1 代码3中Printing()函数调用后可判断并记录最优路径；

2 下文将讲述01背包问题回溯法的顺序执行方法，并通过模板模式整合两种不同的实现方案。