知新_RL

这个屌丝很懒，什么也没留下！

热门标签

栈：01背包问题(带价值) 栈解法/回溯算法递归算法【C语言，数据结构】（内含源代码）_背包问题递归算法

作者：知新_RL | 2024-03-29 01:43:32

踩

背包问题递归算法

题目：

背包问题（Knappsack Problem).

分别设计背包问题的递归算法，和利用栈解决背包问题的非递归算法，分析比较两种算法的时间复杂度和空间复杂度。

需求分析：

1.用递归算法解决背包问题

2.用栈解决背包问题

3.输入两个数代表背包容量与物品个数。然后分两行输入物品重量和价值

例如：


1 2
1 2
2 1

表示，背包容量为1，有两个物品，物品重量是：1和2。物品价值是：2和1。

4.程序执行命令包括：(1)收集输入 (2)用递归计算 (3)用栈计算

5.测试数据：

概要设计：

1.输入数据用两个数组存储。

2.主程序模块：

void main(){

接收输入；

递归处理；

栈处理；

输出；

}

详细设计：

用递归和栈的思想都一样，那就是要试过商品的所有排列组合，找到价值最大的一组。

大概思路就是，模拟用背包去装物品的过程，一个一个遍历物品，如果装得下就装，装不下就跳过这个物品看下一个，装满了就判断，这一种排列组合的商品价值如果大于上一组，就改变记录的最大价值，然后把包里最后一个物品拿出来，选择不装他，接着往下遍历。

递归解法：

递归的核心思想与上述描述也没有太大区别，递归使用一个数组，来保存截止上一个物品，前面的物品能装多大价值，通过前面的结果，计算出第i个物品的结果。

用一个i来表示，截止计算到第i件物品，这个背包对前i件物品的最佳选择，然后传入下一个递归r(i+1)。

最佳选择结果怎么来的？这个也不是什么智能选择，通过比较，背包里装第i件物品，和不装第i件物品，选出价值最大的，就是最佳选择。

为什么不装第i件物品会更好？因为背包空间是有限的，这里指的装意思是，为了一定装下这件物品，我要找到前面背包空间刚好能装下第i件物品的状态，然后把这件物品装进去。不装的意思是，保留前一次最佳的状态，不装该物品。


int GetMaxVR(int sum, int nowWeight, int step, int *w, int *v, int n, int bag) {
	//背包，递归
	int max = 0;
	int maxb = 0;
	if(nowWeight > bag) //超出重量 则回退
		return max;
	if(step == n) { //已经完成n件物品的选择
		if(sum > max)
			max = sum;	// 更新最大价值
		return max;
	}
	max = GetMaxVR(sum + v[step], nowWeight + w[step], step + 1, w, v, n, bag); //选这件物品
	maxb = GetMaxVR(sum, nowWeight, step + 1, w, v, n, bag);					//不选这件物品
	if(max > maxb) {	//结果返回
		return max;
	} else {
		return maxb;
	}
}

如果看代码也不清楚可以看一下这篇博客：

http://t.csdn.cn/U960r

栈解法（回溯算法）：

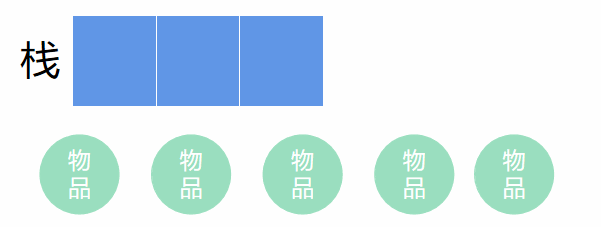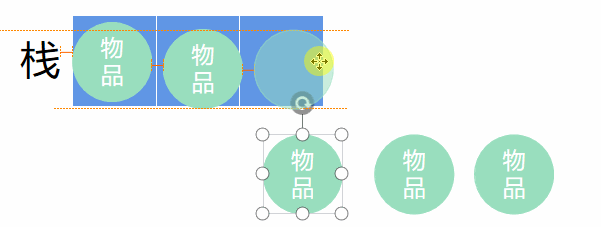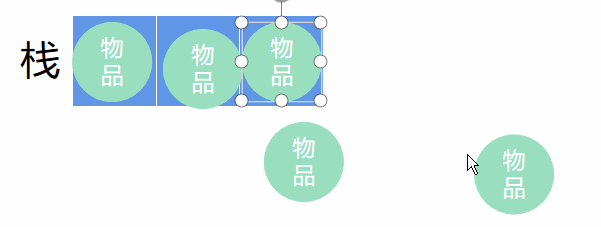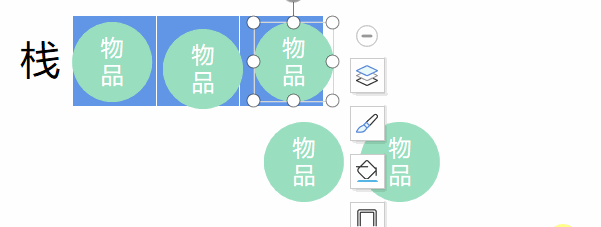
栈的解法就相对更简单了，栈就是我们的背包。

从一开始，把第i件物品放入栈里，如果背包还能装，则装下第i件物品，在判断下一件。

当背包满的时候，就计算背包里的物品价值，大于则记录新最大价值，然后最后一件出栈，把指针i指向弹出的最后一件的下一个物品，这里就代表不装弹出的那一件物品，继续上述操作。

当然还有特殊情况，就是到最后一件了，还没有装满栈。依然重复出栈操作，最后一件出栈，把指针i指向弹出的最后一件的下一个物品，继续向下重复入栈操作。

用图来掩饰就是这样的。


int GetMaxVS(int *w, int *v, int n, int bag) {
	//背包，栈,回溯
	int bagw = 0, bagv = 0, MValue = 0;
	SqStack bagi;
	InitStack(&bagi);
	for(int i = 0; StackEmpty(bagi) != OK || i < n; i++) {
		if(bagw == bag || i >= n) {	//背包满或遍历完，则计算结果，并回溯
			if(bagv > MValue) {
				MValue = bagv;
			}
			Pop(&bagi, &i);
			bagw -= w[i];
			bagv -= v[i];
		} else if(bag >= bagw + w[i]) {	//不满则继续遍历
			Push(&bagi, i);
			bagw += w[i];
			bagv += v[i];
		}
	}
	return MValue;
}

总结：

递归方法还有一种思路，用f[n]个数组来存储选择到第i件物品时的最优价值，这样虽然空间复杂度大了，但更利于人来理解递归是怎么工作的。在这里，我们选用的是机器效率最高的一种递归。

用户手册：

1.本程序为DOS环境。

2.进入后，根据提示输入背包容量、物品个数、物品价值和重量后回车。

3.根据输入，程序会显示两种方法计算到的最大价值结果

（两种方法计算的最大价值应该相同）

测试结果：

源代码：

头文件：


#include <stdio.h>
#include <stdlib.h>
#include <conio.h>
#include <malloc.h>
 
#define TRUE 1	//函数结果状态码
#define FALSE 0
#define ERROR 0
#define OK 1
#define EQUAL 1
#define OVERFLOW -1
#define INFEASIBLE -2
#define STACK_INIT_SIZE 100	//存储空间初始分配量
#define STACKINCREMENT 10	//存储空间分配增量
 
typedef int Status;	//Status 为函数返回值类型，其值为函数结果状态代码
 
typedef int SElemType;	//栈中数据元素类型为int型
 
typedef struct {	//栈的顺序存储表示
	SElemType *base;	//栈构造之前和销毁之后，其值为NULL
	SElemType *top;	//栈顶指针
	int stacksize;	//当前已分配的存储空间
} SqStack;
 
Status InitStack(SqStack *);			//栈初始化
Status DestroyStack(SqStack *);		//销毁栈
Status StackEmpty(SqStack);			//栈判空
Status GetTop(SqStack, SElemType *);	//取栈顶元素
Status Push(SqStack *, SElemType);	//入栈
Status Pop(SqStack *, SElemType *);	//出栈
Status StackTraverse(SqStack);		//遍历栈，输出每个数据元素
 
Status InitStack(SqStack *S) {
	//构造一个空栈Ss
	S->base = (SElemType *)malloc(STACK_INIT_SIZE * sizeof(SElemType));
	if(!S->base) {
		//存储分配失败
		exit(OVERFLOW);
	}
	S->top = S->base;
	S->stacksize = STACK_INIT_SIZE;
	return OK;
}//InitStack
 
Status GetTop(SqStack S, SElemType *e) {
	//若栈不空，则用e返回S的栈顶元素，并返回OK；否则返回ERROR
	if(S.top == S.base) {
		return ERROR;
	}
	*e = *(S.top - 1);
	return OK;
}//GetTop
 
Status Push(SqStack *S, SElemType e) {
	//插入元素e为新的栈顶元素
	if(S->top - S->base >= S->stacksize) {
		//栈满，追加存储空间
		S->base = (SElemType *)realloc(S->base, (S->stacksize + STACKINCREMENT) * sizeof(SElemType));
		if(!S->base) {
			//存储分配失败
			exit(OVERFLOW);
		}
		S->top = S->base + S->stacksize;
		S->stacksize += STACKINCREMENT;
	}
	*S->top++ = e;
	return OK;
}//Push
 
Status Pop(SqStack *S, SElemType *e) {
	//若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK；否则返回ERROE
	if(S->top == S->base) {
		return ERROR;
	}
	*e = *(--S->top);
	return OK;
}//Pop
 
Status DestoryStack(SqStack *S) {
	//销毁栈S
	if(S->base) {
		free(S->base);
	}
	S->top = S->base = NULL;
	return OK;
}//DestroyStack
 
Status StackEmpty(SqStack S) {
	//栈判空
	if(S.base == S.top) {
		return OK;
	}
	return ERROR;
}
 
Status StackTraverse(SqStack S) {
	//遍历栈，输出每一个数据元素
	SElemType *p = S.base;
	int i = 0;
	if(S.base == S.top) {
		printf("Stack is Empty.\n");
		return OK;
	}
	while(p < S.top) {
		printf("[%d:%d]\n", ++i, *p++);
	}
	return OK;
}//StackTraverse

主程序：


#include "SqStack.h"
 
Status input(int **, int **, int *, int *);	//输入程序
int GetMaxVR(int, int, int, int *, int *, int, int);	//背包，递归
int GetMaxVS(int *, int *, int, int);	//背包，栈,回溯
 
int main() {
	int *w, *v;
	int n, bag;
	int maxR, maxS;
	input(&w, &v, &n, &bag);
 
	maxR = GetMaxVR(0, 0, 0, w, v, n, bag);
	maxS = GetMaxVS(w, v, n, bag);
 
	printf("Max value is: %d(stack) and %d(recursion)", maxS, maxR);
	return 0;
}//main
 
Status input(int **w, int **v, int *n, int *bag) {
	//输入程序
	printf("How much can the backpack hold?\n");
	scanf("%d", bag);
	printf("How many objects will there be?\n");
	scanf("%d", n);
	*w = (int *)malloc(sizeof(int) * (*n));
	*v = (int *)malloc(sizeof(int) * (*n));
	printf("Enter weights in order:\n");
	for(int i = 0; i < *n; i++) {
		scanf("%d", *w + i);
	}
	printf("Enter value in order:\n");
	for(int i = 0; i < *n; i++) {
		scanf("%d", *v + i);
	}
	return OK;
}
 
int GetMaxVR(int sum, int nowWeight, int step, int *w, int *v, int n, int bag) {
	//背包，递归
	int max = 0;
	int maxb = 0;
	if(nowWeight > bag) //超出重量 则回退
		return max;
	if(step == n) { //已经完成n件物品的选择
		if(sum > max)
			max = sum;	// 更新最大价值
		return max;
	}
	max = GetMaxVR(sum + v[step], nowWeight + w[step], step + 1, w, v, n, bag); //选这件物品
	maxb = GetMaxVR(sum, nowWeight, step + 1, w, v, n, bag);					//不选这件物品
	if(max > maxb) {	//结果返回
		return max;
	} else {
		return maxb;
	}
}
 
int GetMaxVS(int *w, int *v, int n, int bag) {
	//背包，栈,回溯
	int bagw = 0, bagv = 0, MValue = 0;
	SqStack bagi;
	InitStack(&bagi);
	for(int i = 0; StackEmpty(bagi) != OK || i < n; i++) {
		if(bagw == bag || i >= n) {	//背包满或遍历完，则计算结果，并回溯
			if(bagv > MValue) {
				MValue = bagv;
			}
			Pop(&bagi, &i);
			bagw -= w[i];
			bagv -= v[i];
		} else if(bag >= bagw + w[i]) {	//不满则继续遍历
			Push(&bagi, i);
			bagw += w[i];
			bagv += v[i];
		}
	}
	return MValue;
}

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/知新_RL/article/detail/332929

栈：01背包问题(带价值) 栈解法/回溯算法 递归算法【C语言，数据结构】（内含源代码）_背包问题递归算法

题目：

需求分析：

概要设计：

详细设计：

递归解法：

栈解法（回溯算法）：

总结：

用户手册：

测试结果：

源代码：

栈：01背包问题(带价值) 栈解法/回溯算法递归算法【C语言，数据结构】（内含源代码）_背包问题递归算法