Incorporating Knowledge Graph Embeddings into Topic Modeling_vmf分布

---

---

   DF-LDA(Dirichlet Forest LDA)模型能以必须链接和不能链接用户输入的形式合并知识。 必须链接表示两个单词应该共享同一主题，而不能链接表示两个单词不应该出现在同一主题中。(2011)提出了两种贝叶斯正则化方法来提高话题连贯性。 这两种方法都利用了额外的单词共现数据来提高学习主题的可解释性。

    (基于常识的LDA)GK-LDA可以使用来自多个领域的必须链接知识。(2015)通过建立马尔可夫随机场正则化将单词相关性纳入LDA。 为了自动学习单词相关知识，提出了AMC（具有自动生成的Must-link和Cannot-links的主题建模）。AMC可以从多个域中自动学习必须链接或不能链接的知识，以改善每个域中的主题建模。

    ②单词语义类别知识

    (2009)提出了主题固定的知识，该知识将单词的主题分配限制为主题的子集。 同样，(2008)提出了Concepttopic模型，通过利用具有层次结构的人类定义概念来分配单词的主题。(2011)提出了一个框架，允许用户强制一组单词必须同时出现在同一主题中的约束来迭代地优化主题。(2012)建议通过设置一组用户认为可以代表某些主题的种子词来指导主题建模。 最近,（2015年）提出了一种通过利用受控的结构化词汇来实现可解释性的方法，在该结构化词汇中，单词被组织成树状结构的层次结构。

    ③其他知识形式

    （2011)通过结合由一阶逻辑指定的一般知识来扩展集合中的主题知识。 最近，ProbaseLDA(2015)，提出了一种将主题模型和概率知识库相结合的方法。 该方法可以在考虑概率知识库的情况下对文本内容进行建模，以发现更好的主题。（2015)将LDA与从文档相对相似性得出的约束联系起来。 (2016)首次将统计主题表示与结构实体分类相结合，为准确归纳基础语义提供了一种有用的方案。

最近的一些作品使用了单词嵌入(Mikolov2013)来编码语义规则。(2015)用词嵌入空间上的多元高斯分布取代了LDA对“主题”的参数化，将其作为词上的范畴分布，其中语义相似度是通过 词向量的欧几里德距离来衡量的。 最近，(Batmanghelich2016)提出使用von Mises-Fisher分布 对非参数主题模型中的词向量之间的余弦距离进行建模。 这些方法启发我们将先验知识以知识图的形式嵌入到主题建模中。

    尽管上述基于知识的主题模型在很多方面利用了知识，但 它们不能处理大规模面向事实的三元知识图中的知识。 在这项工作中，我们关注的是这种被广泛使用的知识形式。

  【基于知识的主题模型】

    一个典型的知识图通常将知识描述为多关系数据，并将知识表示为三个事实(头实体、关系实体、尾实体)，这表明了两个实体之间的关系。

知识图嵌入的目标是将知识图的实体和关系嵌入到向量空间中。 将知识图嵌入到低维连续向量空间中，同时保留了图的某些性质。 通常，每个实体被视为向量空间中的一个点，每个关系被视为实体嵌入上的操作。 例如，Transe(2013)将关系解释为从头实体到尾实体的转换。 嵌入向量通常通过最小化所有实体和关系的全局损失函数来获得，从而使每个实体向量同时捕获原始知识图的全局和局部结构模式，从而可以利用实体嵌入对主题建模的先验知识进行编码。

    

    

2.方法

---

    在这一部分中，我们介绍了KGE-LDA模型、Gibbs抽样推理和参数学习方法。

    我们通过扩展两个经典的实体主题模型将实体嵌入到主题建模中，这两个模型分别是CI-LDA和Corr-LDA。 这两个模型可以处理同一主题空间中的词和实体，但它们只考虑在文本中识别的命名实体。 为了在知识图中利用三元组，我们可以直接使用实体嵌入来编码知识图结构，而不是只对实体进行编码。

    由于余弦距离通常用于度量实体嵌入之间的相似性，并且一些知识图嵌入位于单位球面上，我们使用von Mises-Fisher(VMF)分布对它们进行建模。 VMF是定义单位球面上的点上的概率密度的分布。 vmf分布的概率密度函数是

 其中在一维球面上，即。μ是平均值参数，(κ>0)k是浓度参数，前者定义平均值的方向，后者决定平均值周围概率质量的分布.。是阶为ν，变元为a的第一类修正的贝塞尔函数。是x与均值μ之间的余弦相似度，κ的作用是方差的倒数。

(1)表征与生成过程

    我们将基于CI-LDA的模型命名为KGE-LDA(A)，将基于Corr-LDA的模型命名为KGE-LDA(B)

   设D是文档的个数，其中每个文档d有词，实体通过现有的实体链接工具链接到现有的知识图，是d文档中的第n个词，是d中第m个实体的L维实体嵌入，这是本文通过横截(一维面)得到的。 我们选择Transe是因为它简单有效，并且在编码知识方面达到了最先进的性能。 而且，横截面的实体向量自然具有单位范数，不需要进行后处理。 分别是和的潜在主题分配。 设K是主题的个数，φk是主题的V维主题词多项式，其中V是词汇表大小，θd是d的K维文档主题多项式。由于我们的实体是单位球面上的连续向量，我们将每个实体主题表征为具有参数的vmf分布。 α和β分别是θd和φk上的Dirichlet先验的超参数。 μ0，C0是μk的先前vmf分布的超参数。 是的先前对数正态分布的均值和标准差。

    ①KGE-LDA(a)

    

    ②KGE-LDA(b)

                                                                        

(2)推理与参数学习

    我们使用Gibbs抽样来推断潜在主题赋值和。的Gibbs抽样方程定义为：

        

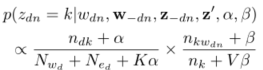
    其中k是主题，w−dn是除wdn之外的所有单词，z−dn是除wdn之外的所有单词的主题分配，z' 是所有实体的主题分配，是主题k被分配给文档d中的词或实体的次数，是wdn被分配给主题k的次数，是所有词被分配给主题k的总次数。

    的Gibbs抽样方程类似中的Gibbs抽样。 我们可以利用vMF分布是共轭来抽样。 这使我们能够完全集成μk并仅通过维护主题赋值变量来更新模型。KGE-LDA(a)推断等式：

    

其中是除edm之外的所有实体的主题分配，是除edm之外的所有实体的嵌入，z是所有单词的主题分配，是任何实体被分配给主题k的次数。如果我们将L和κk替换为l和κ，则C1(κk)的含义与等式(1)中的C1(κ)相同。 由于κk来自对数正态分布，我们首先从κk样本中抽取一些κk样本(在我们的实验中

  KGE-LDA(b)如下：

    

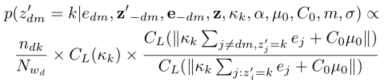
    通过吉布斯抽样，我们可以使用公式(2)中的两个因子来估计θd和φk。

    

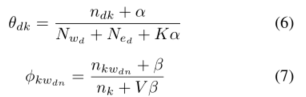
是100个样本，我们也尝试了其他的数字，但没有发现太大的差别)，然后使用公式(4)从这些样本中抽取最终的Log k样本。

 

3.总结

---

    本文提出了一种将主题模型和知识图嵌入相结合的KGE-LDA，特别是LDA模型和TRASE。 该方法利用自动从外部知识图学习到的实体向量编码的知识对文档级词语共现进行建模，可以提取更连贯的主题和更好的主题表示。 在三个数据集上的实验结果表明了该方法的有效性。 我们计划在未来的工作中探索更有效的方法来整合实体嵌入和试验更多的知识图。