程序员算法趣味题：落单的男女_程序员趣味问答

题目

暴力解法

大概需要运行个一两分钟

#include<bits/stdc++.h>
using namespace std;
bool check(vector<int>&v,int l,int r);
bool dfs(vector<int>&v,int k){
    if(k==v.size()-1) return true;
    if(check(v,0,k)||check(v,k+1,(int)v.size()-1))
        return false;
    return dfs(v,k+1);
}
bool check(vector<int>&v,int l,int r){
    int cnt1 = 0,cnt2 = 0;
    for(int i=l;i<=r;i++) {
        if(v[i]==1)
            cnt1++;
        else if(v[i]==0)
            cnt2++;
    }
    return cnt1==cnt2;
}
int main(){
    int n,m;
    cin>>n>>m;
    int res = 0;
    vector<int> v(m+n);
    for(int i=0;i<n;i++)v[i]=0;
    for(int i=n;i<m+n;i++)v[i]=1;
    if(dfs(v,0))
        res++;
    while(next_permutation(v.begin(),v.end())){
        if(dfs(v,0))
            res++;
    }
    cout<<res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

方块走步模拟人员到来

• 用数组坐标的移动模拟男女出席的过程。
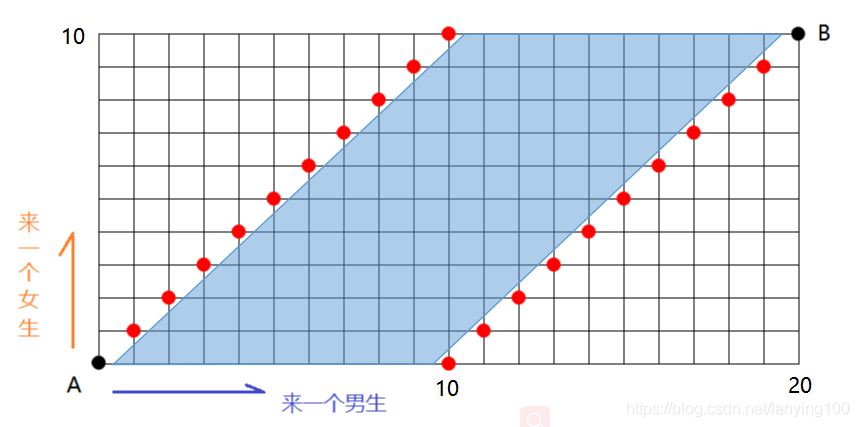
  • 这个动态规划解法的含义就是：用网格来代替男女的入场顺序，从起点（0,0）此时还没有任何人到场，如果y轴+1则代表此时来了一个女生，相对的如果x轴+1则代表来了个男生，就这样从起点每次走一步，只能x+1或者y+1，相当于只能往上或者往右走动，一直移动到男女人数都来齐了这就是一个先后组合，从图上来看的话，就是从起点到终点的路径条数。当然增加人数的过程中不允许出现人数相等的情况(一旦出现则说明可以分出男女相同的组)。
  • 由于每一个到达的点位是当前所到达的状态(就是当前来了多少人)，所以有以下两种情况会出现男女相同的组：
  1. x = y.
  2. n-x = m-y,这种情况说明所有人到达后，我们在这个点进行分割，则剩余的那部分男女是相等的。

有了以上解析做铺垫，则解答本题只需要转换为计算(0,0)到(n,m)的所有路径条数中不经过相等点的路径条数。就是下面图中的阴影区域了(在阴影区域外则必会经过相等点)。

1ms解决…

#include<bits/stdc++.h>
using namespace std;
int main(){
    int n,m;
    //大的数字作为横轴(x轴=>列)，小的数字作为纵轴(y轴=>行)
//    cin>>n>>m;
    n = 10;m = 20;
    int dp[n+1][m+1];
    memset(dp,0,sizeof dp);
//更新阴影区域的第一行。
    for(int i=0;i<m-n;i++)dp[0][i] = 1;
    //只更新阴影区域
    for(int i=1;i<=n;i++){
        for(int j=i+1;j<m-n+i;j++){
            dp[i][j] += dp[i-1][j];
            dp[i][j] += dp[i][j-1];
        }
    }
    cout<<dp[n][m-1];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

对路径问题的一些认识

实际上路径问题就是排列问题，很多情况下两者可以互换。

横向 4 步、纵向 3 步地移动也就是“7 步中有 4 步为横向移动”，数学上就是 C^7_4 计算可得 35 种情况。本题用的是通过反复统计从最左列和最下列到达各个交叉点的情况，得到最终解的方法。对于复杂图形而言，这是一种行之有效的方法。