Guff_9hys

这个屌丝很懒，什么也没留下！

热门标签

Matlab：线性规划_linprog(f,a,b)

作者：Guff_9hys | 2024-07-18 07:18:12

踩

linprog(f,a,b)

注：

1、x = linprog(f,A,b) ;求解 min f'*x，满足 A*x ≤ b;

例：

$x_{1}+2x_{2}\leqslant 6$

$2x_{1}-\frac{1}{2}x_{2}\leq 3$

$-x_{1}-x_{2}\leq 3$

$f=x_{2}$


A=[1,2;2,-1/2;-1,-1];
b=[6,3,3];
f=[0,1];
x=linprog(f,A,b)

2、x = linprog(f,A,b,Aeq,beq) ;包括等式约束 Aeq*x = beq。如果不存在不等式，设置 A = [] 和 b = [];

例：

$x_{1}+x_{2}\leqslant \frac{1}{4}$

$x_{2}+x_{3}\leqslant \frac{1}{2}$

$x_{1}+x_{2}-x_{3}\leqslant \frac{1}{3}$

$x_{1}+x_{2}+x_{3}=1$

$f=-x_{2}+x_{3}$


A=[1,1,0;0,1,1;1,1,-1];
b=[1/4,1/2,1/3];
Aeq=[1,1,1];
beq=1;
f=[0,-1,1];
x=linprog(f,A,b,Aeq,beq)

3、x = linprog(f,A,b,Aeq,beq,lb,ub) ;定义变量 x 的一组下界和上界，使解始终在 lb ≤ x ≤ ub 范围内。如果不存在等式，设置 Aeq = [] 和 beq = []。

例：

$x_{1}+x_{2}+x_{3}\leqslant 2$

$x_{1}+4x_{2}\leqslant 4$

$3x_{2}-x_{3}\leq 3$

$f=-x_{2}+x_{3}$

$-2\leqslant x_{1}\leqslant 5$

$-1\leqslant x_{2}\leqslant 4$

$-3\leqslant x_{3}\leqslant 4$


A=[1,1,1;1,4,0;0,3,-1];
b=[2,4,3];
f=[0,-1,1];
lb=[-2,-1,-3];
ub=[5,4,4];
x=linprog(f,A,b,[],[],lb,ub)

4、[x,fval] = linprog(f,A,b)；求解问题并返回函数值。

options = optimoptions('linprog','Algorithm','dual-simplex');设置选项以使用 'dual-simplex' 算法。

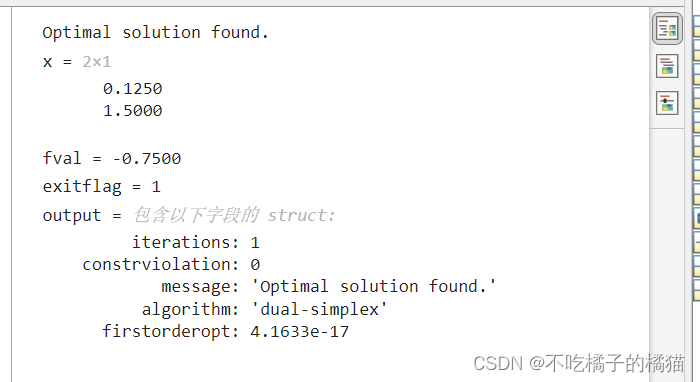
[x,fval,exitflag,output] = linprog(f,A,b,Aeq,beq,lb,ub,options);求解线性规划并请求返回函数值、退出标志和输出结构体。

注：

（1）exitflag = 1 表示解可靠；

（2）output.iterations = 0 表示 linprog 在预求解过程中即找到解，根本不必进行迭代。

例：

$x_{1}+x_{2}\leqslant 2$

$x_{1}+0.25x_{2}\leqslant 1$

$x_{1}-x_{2}\leqslant 2$

$-0.25x_{1}-x_{2}\leqslant 1$

$-x_{1}-x_{2}\leqslant -1$

$-x_{1}+x_{2}\leqslant 2$

$x_{1}+0.25x_{2}=0.5$

$-1.5\leqslant x_{1}\leqslant 1.75$

$-1\leqslant -x_{2}\leqslant 1.5$

$f=-1.2x_{1}-0.4x_{2}$


A=[1,1;1,0.25;1,-1;-0.25,-1;-1,-1;-1,1];
b=[2,1,2,1,-1,2];
Aeq=[1 0.25];
beq=0.5;
lb=[-1.5,-1];
ub=[1.75,1.5];
f=[-1.2 -0.4];
options=optimoptions('linprog','Algorithm','dual-simplex');
[x,fval,exitflag,output]=linprog(f,A,b,Aeq,beq,lb,ub,options)

5、拉格朗日乘数

例：

$f=-5x_{1}-4x_{2}-3x_{3}$

$x_{1}-2x_{2}+x_{3}\leqslant 20$

$3x_{1}+2x_{2}+4x_{3}\leqslant 42$

$3x_{1}+2x_{2}\leqslant 31$

$x_{1}\geqslant 0$

$x_{2}\geqslant 0$

$x_{3}\geqslant 0$


f=[-5;-4;-3];
A=[1,-2,1;3,2,4;3,2,0];
b=[20;42;31];
lb = zeros(3,1);  %把三个变量均约束为正值
Aeq=[];           
beq=[];           %没有线性等式约束
[x,fval,exitflag,output,lambda] = linprog(f,A,b,Aeq,beq,lb); %调用linprog，获取拉格朗日乘数
x,lambda.ineqlin,lambda.lower   %检查解和拉格朗日乘数
A*x             %检查这是否属实

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/Guff_9hys/article/detail/844219