机器学习 KNN算法_最近邻思想

参考B站简博士

一、KNN基本概念

最近邻（k-Nearest Neighbors, KNN）算法是一种分类算法，该算法的思想是：一个样本与数据集中的k个样本最相似，如果这k个样本中的大多数属于某一个类别，则该样本也属于这个类别。

二、距离度量

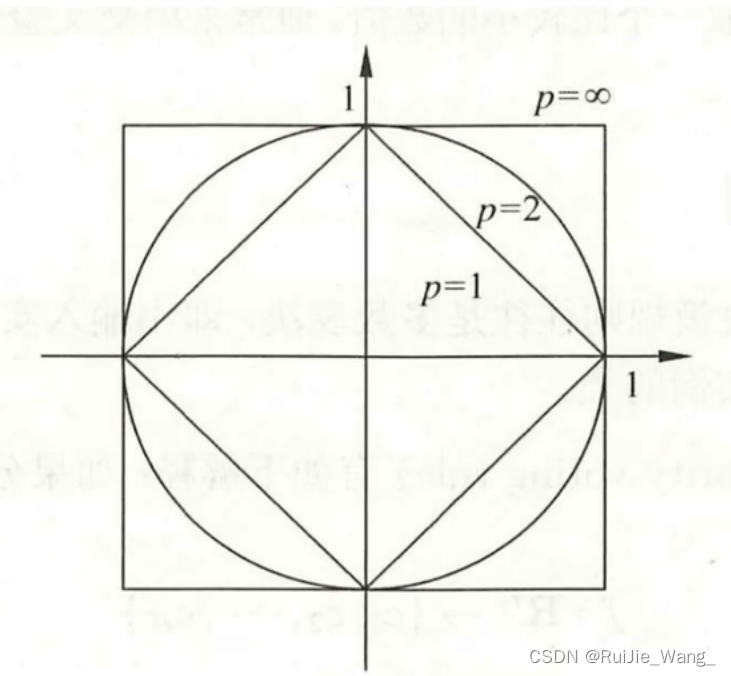
一般使用欧式距离来衡量两个实例点的相似性。

Lp距离：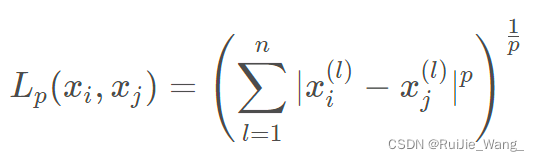                

欧式距离：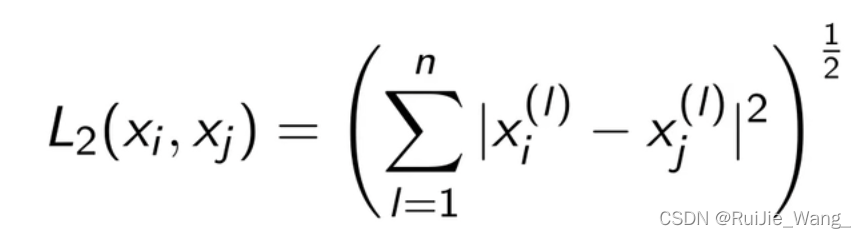 

 

 曼哈顿距离：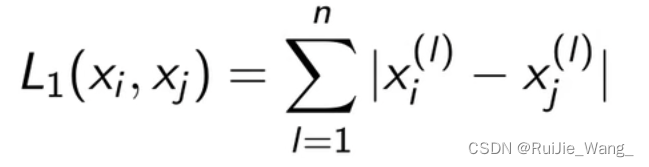

切比雪夫距离：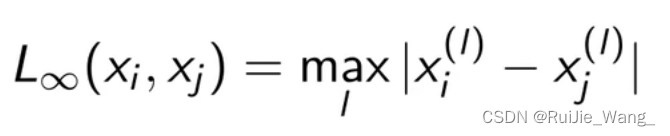 

 

三、K值选择

如果选择较小的K值，训练误差会减小，但测试误差可能会增大，因为预测结果会对近邻的实例点成分敏感，如果邻近的实例点是噪声，预测就会错。K值减小导致模型变复杂，容易过拟合。

如果选择较大的K值，可以减小测试误差，但模型可能过于简单。

四、分类决策规则

多数表决规则：由输入实例的k个邻近的训练实例中的多数类决定输入实例的类。

五、构造kd树

1.构造kd树：算法

输入：k维空间数据集：

其中，

输出：kd树

（1）开始：构造根节点。

选取第一个特征为坐标轴，以训练集中的所有数据x(1)坐标中的中位数作为切分点，将超矩形区域切割成两个子区域，将该切分点作为根节点。

由根结点生出深度为1的左右子节点，左节点对应坐标小于切分点，右节点对应坐标大于切分点。

 （2）重复：

对深度为j的节点，选择x(L)为切分坐标轴，L=j(mod k) + 1, 以该节点区域中所有实例X(L)坐标的中位数作为切分点，将区域分为两个子区域。

生成深度为j + 1的左、右子节点。左节点对应坐标小于切分点，右节点对应坐标大于切分点。

 （3）直到两个子区域没有实例时停止。

2、例子

输入：训练集：

输出：kd树

 

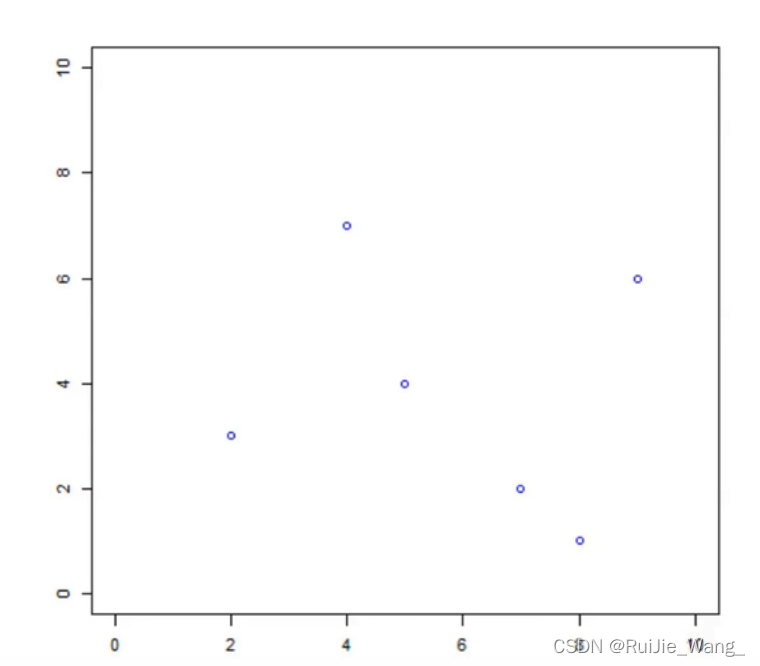
 x(1) : 2, 4, 5, 7, 8, 9

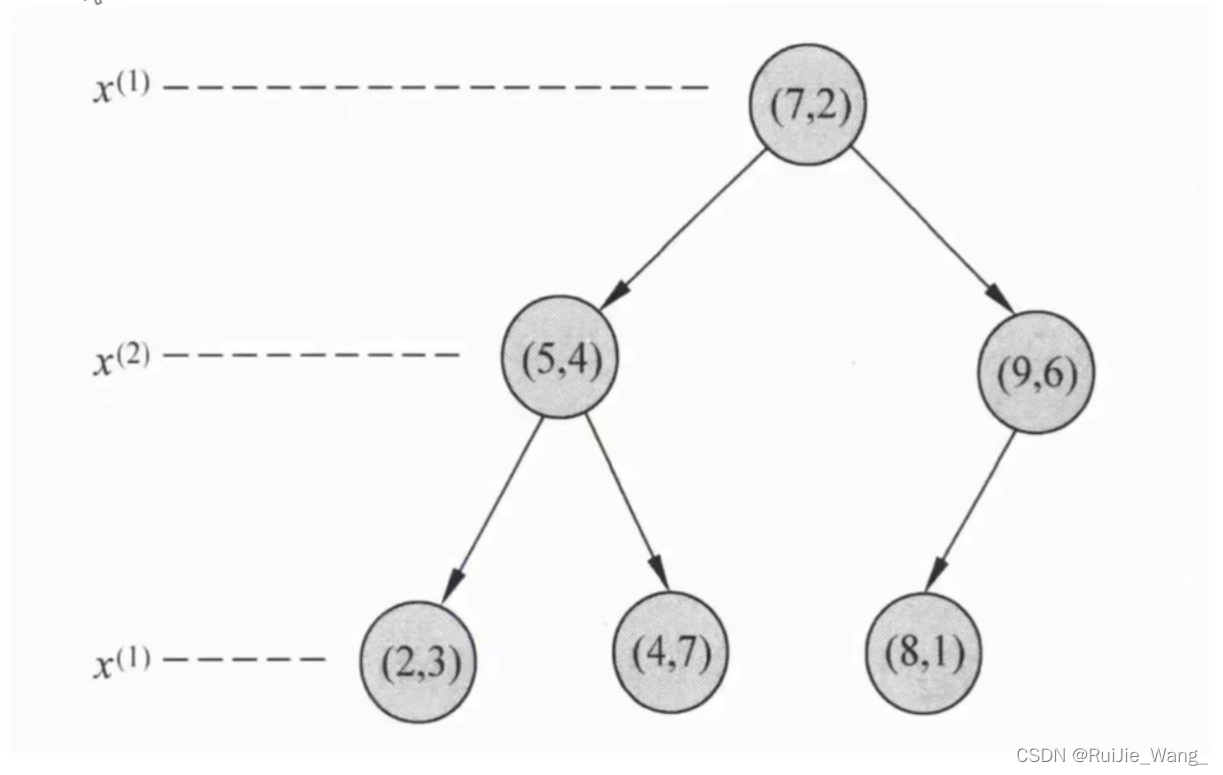
开始：选择x(1)为坐标轴，中位数为7，即(7,2)为切分点，切分整个区域。

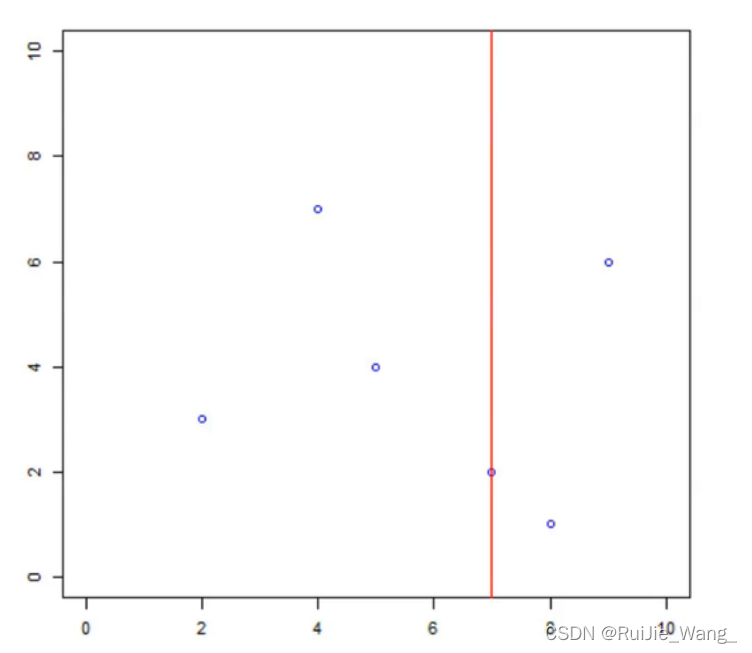
 再次划分区域：

以x(2)为坐标轴，选择中位数，左边区域为4，右边区域为6。因此左边区域切分点为（5，4），右边区域切分点为（9， 6）

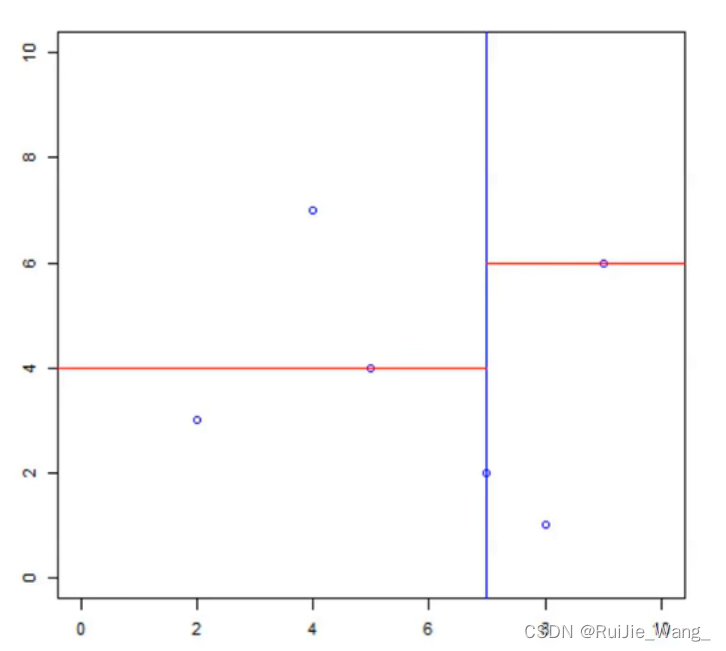
划分左边区域：

 以x(1)为坐标轴，选择中位数，上边区域为4，下边区域为2。故上边区域切分点为(4, 7), 下边区域切分点为（2，3）

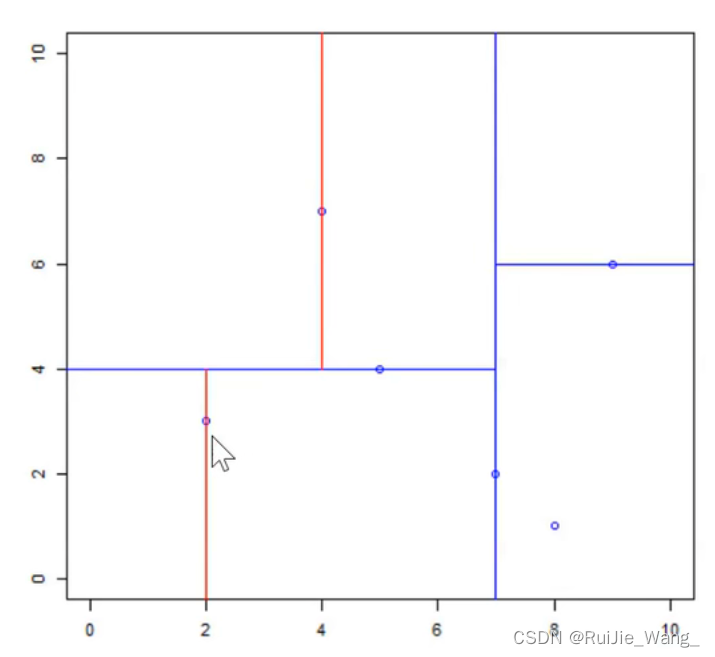
 划分右边区域：

以x(1)为坐标轴，选择中位数，上边区域无实例点，下边区域为8。故下边区域划分点坐标为（8,1 ）

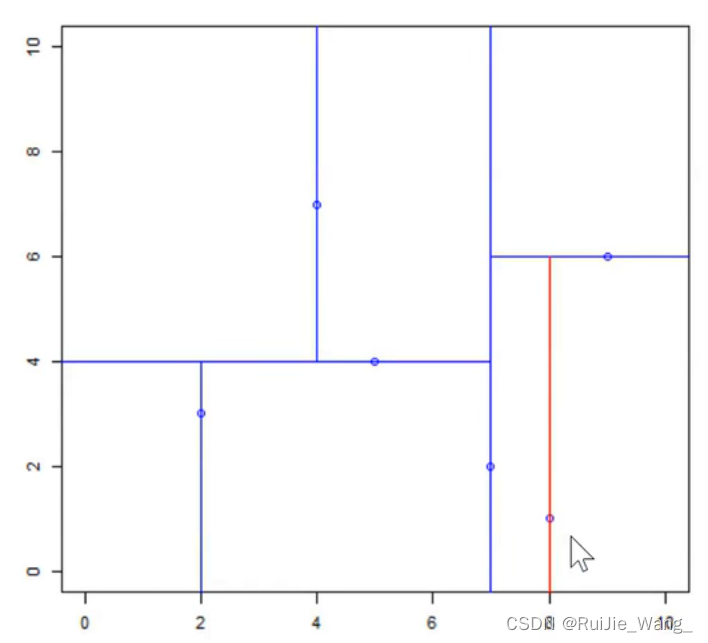
输入：训练集：

输出：kd树

 六、搜索kd树

1、最近邻搜索：算法

输入：已构造的kd树， 目标点x

输出：x的最近邻

寻找“当前最近点”

        -从根节点触发，递归访问kd树，找出包含x的叶节点；

        -以此叶节点为“当前最近点”；

回溯

        -若该节点比“当前最近点”距离目标点更近，更新“当前最近点”；

        -当前最近点一定存在于该节点一个子节点对应的区域，检查子节点的父节点的另一子   节点对应的区域是否有更近的点。

当回退到根节点时，搜索结束，最后的“当前最近点”即为x的最近邻点。

        

2、例题

输入：kd树(下图所示）， 目标点x=(2.1, 4.5);

输出：最近邻点

最近邻点（4，7），第一次回溯，这里的圆圈就是实例点和当前最近邻点的欧式距离作为半径。

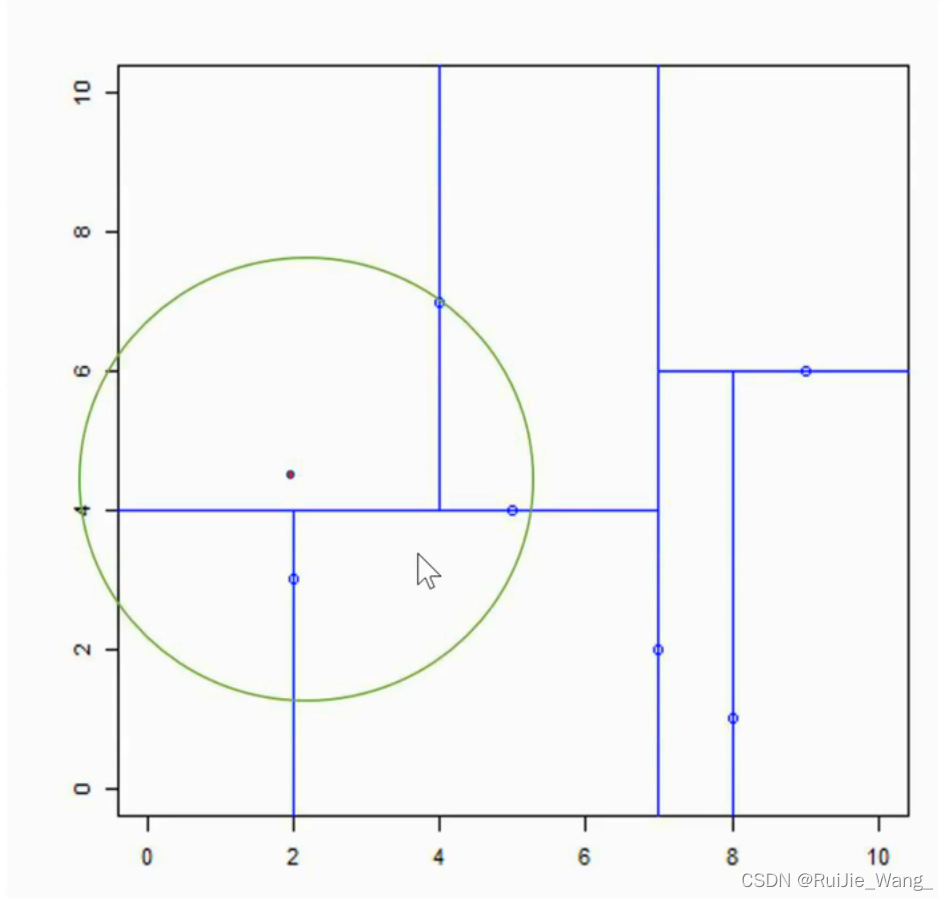
 回溯的过程就是从子节点到父节点，再到父节点的父节点，在这个过程中，检查这个圆圈里的点和实例点的距离，更新最近邻点为（2， 3）

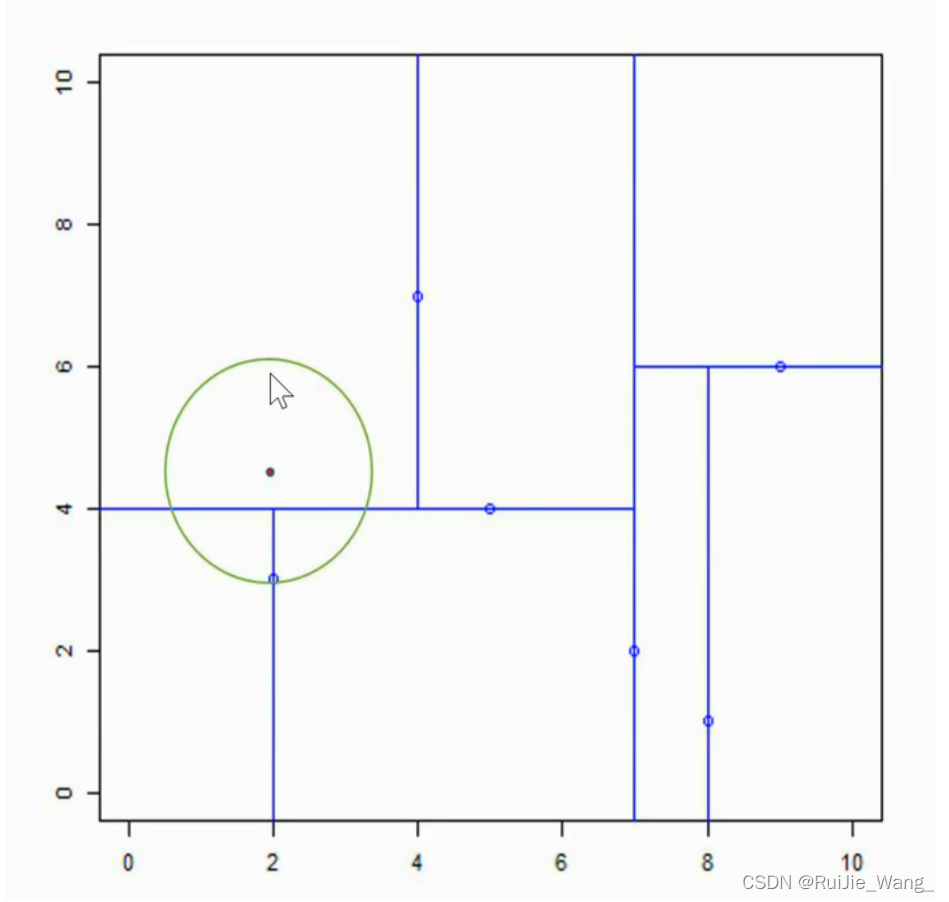
 没有交集了，那么最近邻点就是（2, 3）