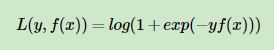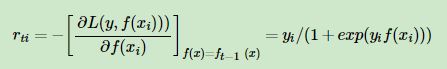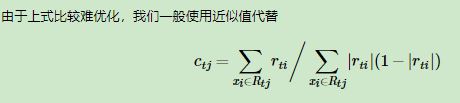- 1IntenLM2-三-《“茴香豆“:零代码搭建你的 RAG 智能助理》
- 2springboot集成mqtt(emqx)_springboot emqx
- 3Spring Boot 和 Spring Cloud 的区别及选型_spring boot和cloud
- 4mysql表连接和子查询效率_mysql left join 与子查询的性能比较 例子
- 5python入门3数学功能函数_round(x,y)方法返回保留y位小数的x值
- 6ADRV9009的JESD204接口传输_serdout
- 7RabbitMQ 6种应用场景_rabbitmq 使用场景
- 8基于深度学习的知识图谱构建(简要综述)_webnlg数据集介绍
- 9[ELK实战] Elasticsearch 聚合查询二: Bucketing/桶聚合_elk es查询时间查询
- 10使用div+css实现表格布局_div实现表格布局
Gradient Boosting Decision Tree (GBDT)
赞
踩
GBDT也是集成学习Boosting家族的成员,Boosting是各个基学习器之间有很强的依赖关系,即串行。
Boosting可以分为两类:
- Adaboost: 改变样本的权重
- Gradient Boosting: 用负梯度做残差的估计
GBDT是一个加法模型,采用前向分步算法进行求解。假设前一轮得到的模型是 f t − 1 ( x ) f_{t-1}(x) ft−1(x),损失函数是 L ( y , f t − 1 ( x ) ) L(y, f_{t-1}(x)) L(y,ft−1(x)),本轮迭代的目标是 min L ( y , f t ( x ) ) \min L(y,f_t(x)) minL(y,ft(x)),其中 f t ( x ) = f t − 1 ( x ) + h t ( x ) f_t(x)=f_{t-1}(x)+h_t(x) ft(x)=ft−1(x)+ht(x)。
Freidman提出用损失函数的负梯度作为残差的估计。
GBDT回归算法如下:
GBDT用的是CART回归树,因此GBDT如何做分类变成了CART回归树如何做分类。
二元GBDT分类算法
对数似然损失函数如下:(y为1或-1)
注意和logistic regression损失函数(y为1或0)本质是一样的
负梯度:
用第m棵回归树去拟合负梯度:
预测的时候, 1 1 + e x p ( − f ( x ) ) \frac{1}{1+exp(-f(x))} 1+exp(−f(x))1,其中 f ( x ) 为 多 颗 决 策 树 的 和 f(x)为多颗决策树的和 f(x)为多颗决策树的和
多元GBDT分类算法
K分类,那么每次迭代要生成K棵树。
[1] https://www.cnblogs.com/ModifyRong/p/7744987.html
[2] https://blog.csdn.net/Liangjun_Feng/article/details/80668461