基础算法之——【动态规划之路径问题】1_动态规划寻找所有路径

今天更新动态规划路径问题1，后续会继续更新其他有关动态规划的问题！动态规划的路径问题，顾名思义，就是和路径相关的问题。当然，我们是从最简单的找路径开始！

• 动态规划的使用方法：
  1.确定状态并定义状态数组：（i，j）代表什么意思？dp[i][j]又是什么意思？
  2.确定状态转移方程，即递推公式
  3.确定边界条件并初始化
  4.确定遍历顺序
  5.状态转移
  6.输出结果

---

---

一、LC 62 不同路径

LC 62 不同路径
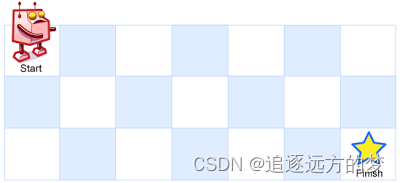
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

---

方法一：深度优先搜索

代码如下：

class Solution {
private:
    int dfs(int m,int n,int i,int j){

        //行或列有至少一个越界
        if(i>m||j>n) return 0;

        //到达终点(在竖直方向达到m，水平方向达到n，也即坐标达到（m,n))
        if(i==m && j==n) return 1;

        //递归搜索（左子树和右子树）
        return dfs(m,n,i+1,j)+dfs(m,n,i,j+1);
    }
public:
    int uniquePaths(int m, int n) {
        
        //从根节点开始遍历
        int cnt=dfs(m,n,1,1);
        return cnt;

    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

---

方法二：动态规划（二维）

代码如下：

/*动态规划的使用方法：
1.确定状态并定义状态数组：（i，j）代表什么意思？dp[i][j]又是什么意思？
2.确定状态转移方程，即递推公式
3.确定边界条件并初始化
4.确定遍历顺序
5.状态转移
6.输出结果
*/
class Solution {

public:
    int uniquePaths(int m, int n) {
        //定义一个状态数组，用来存方法数      
        int dp[101][101]={0};

        //初始化状态数组
        for(int i=0;i<m;i++){
            dp[i][0]=1;
        }
        for(int j=0;j<n;j++){
            dp[0][j]=1;
        }

        //遍历
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                //状态转移
                dp[i][j]=dp[i][j-1]+dp[i-1][j];
            }
        }

        //返回结果
        return dp[m-1][n-1];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

---

方法三：动态规划（一维）

代码如下：

class Solution {
public:
    int uniquePaths(int m, int n) {
          
        //定义一维状态数组  
        int dp[101]={0};

        //初始化数组值为1，即相对于二维数组第一行全是1
        for(int i=0;i<n;i++){
            dp[i]=1;
        }

        //遍历
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                
                //状态转移：dp[j]指的是上一行的j,dp[j-1]指的是当前行左边的j；
                //每次状态转移都相当于先将上一行的运算拷贝过来，再加上从左面来的方案数
                dp[j]=dp[j-1]+dp[j];
            }
        }

        return dp[n-1];
      
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

---

方法四：排列组合

代码如下：

class Solution {
public:
    int uniquePaths(int m, int n) {
        long long numerator = 1; // 初始化分子

        int denominator = m - 1; // 初始化分母

        int count = m - 1;//定义分子的乘积项的个数

        int t = m + n - 2;//定义分子的最大乘积项

        while (count--) {//分子累乘count项

            numerator *= (t--);
            while (denominator != 0 && numerator % denominator == 0) {

                //约分（也即除以公因数）
                numerator /= denominator;

                //约去一个公因数
                denominator--;
            }
        }
        return numerator;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

---

二、LC 63 不同路径II

LC 63 不同路径II
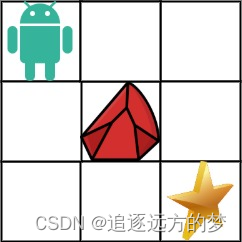
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

---

---

方法一：动态规划（二维）

代码如下：

 class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {

        //求出二维动态数组的行数
        int m=obstacleGrid.size();

        //求出二维动态数组的列数
        int n=obstacleGrid[0].size();

        //定义状态数组
        int dp[101][101]={0};
        
        //边界判断
        if(obstacleGrid[0][0]==1 || obstacleGrid[m-1][n-1]==1) return 0;

        //初始化状态数组
        dp[0][0]=1;

        //遍历
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                
                //如果是障碍物，则此路不通，路径数归零
                if(obstacleGrid[i][j]==1){
                     dp[i][j]=0;
                     continue;
                }

                //状态转移，此处和上面的一样
               if(i>0 && j>0) dp[i][j]=dp[i-1][j]+dp[i][j-1];
               else if(i>0) dp[i][j]=dp[i-1][j];
               else if(j>0) dp[i][j]=dp[i][j-1];

//也可以这样写
/*
 if(obstacleGrid[i][j]==0){
                      //状态转移，此处和上面的一样
               if(i>0 && j>0) dp[i][j]=dp[i-1][j]+dp[i][j-1];
               else if(i>0) dp[i][j]=dp[i-1][j];
               else if(j>0) dp[i][j]=dp[i][j-1];

                }
              
            }
            else continue;
*/
            }
        }
        return dp[m-1][n-1];

    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

---

方法二：动态规划（一维）

代码如下：

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        if (obstacleGrid[0][0] == 1)
            return 0;
        vector<int> dp(obstacleGrid[0].size(),0);
        
        //初始化一维状态数组（第一行）
        for (int j = 0; j < dp.size() && obstacleGrid[0][j] == 0 ; ++j)
            if (j == 0)
                dp[j] = 1;
            else
                dp[j] = dp[j-1];

        //
        for (int i = 1; i < obstacleGrid.size(); ++i)//行
            for (int j = 0; j < dp.size(); ++j){//列

                if (obstacleGrid[i][j] == 1)
                    dp[j] = 0;

                else if (j != 0)
                    dp[j] = dp[j] + dp[j-1];
            }
        return dp.back();//返回最后一个状态对应值
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

---

方法三：记忆化搜索

代码如下：

class Solution {
public:
    int m,n;
    vector<vector<int>>memo;
    vector<pair<int,int>>dir{{0,1},{1,0}};
    int uniquePathsWithObstacles(vector<vector<int>>& ob) {
            n=ob.size();
            m=ob[0].size();
            if(ob[0][0]==1||ob[n-1][m-1]==1){
                return 0;
            }
            memo.resize(n,vector<int>(m,0));
            return dfs(ob,0,0);
    }
    int dfs(vector<vector<int>>&ob,int i,int j){
        if(memo[i][j]!=0){
            return memo[i][j];
        }
        if(i==n-1&&j==m-1){
            memo[i][j]=1;
            return 1;
        }
        int cur=0;
        for(auto &d:dir){
            int x=i+d.first;
            int y=j+d.second;
            if(x>=0&&x<n&&y>=0&&y<m&&ob[x][y]==0){
                cur+=dfs(ob,x,y);
            }
        }
        memo[i][j]=cur;
        return memo[i][j];
    }
};

作者：Gallant MurdockrFZ
链接：https://leetcode.cn/problems/unique-paths-ii/solutions/2466610/dfsji-yi-hua-sou-suo-by-gallant-murdockr-e882/
来源：力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

---

三、LC 64 最小路径和

LC 64 最小路径和
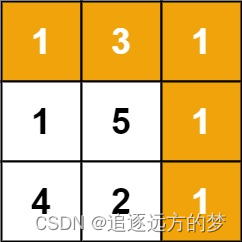
给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

---

方法一：动态规划（二维）

代码如下：

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {

        //定义一个二维状态数组
        int dp[201][201]={0};

        //初始化状态数组
        dp[0][0]=grid[0][0];

        //获得行数和列数
        int m=grid.size();
        int n=grid[0].size();

        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){

                //正常情况
                if(i>0 && j>0){
                    dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j];
                }

                //边界条件
                else if(i>0) dp[i][j]=dp[i-1][j]+grid[i][j];
                else if(j>0) dp[i][j]=dp[i][j-1]+grid[i][j];

            }
        }
        return dp[m-1][n-1];

    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

---

方法二：动态规划（一维）

代码如下：

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {

        //获取行数和列数
       int m=grid.size();
       int n=grid[0].size();

        //定义一维状态数组
       int dp[201]={0};

       //初始化第一行
       dp[0]=grid[0][0];
       for(int i=1;i<n;i++){
           dp[i]=grid[0][i]+dp[i-1];
       }

        //状态转移（配合滚动数组优化）
       for(int i=1;i<m;i++){
           for(int j=0;j<n;j++){
               //左边界
               if(j==0) dp[j]+=grid[i][j];

               //其他情况
               else dp[j]=min(dp[j-1],dp[j])+grid[i][j];
           }
       }
       return dp[n-1];

    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

---

我以前没怎么接触过动态规划，目前就是每天有空看看题，想想解题思路啥的，但愿有效果吧！