- 1RabbitMQ入门_rabbitmq 开启mqtt后没有15675端口
- 2uniapp保存修改个人信息后,使用uni.navigateBack(),返回上一页,没有消息提示,但是已经写过消息提示代码
- 3Stable Diffusion教程:4000字说清楚图生图_stable diffusion拉伸、裁剪、填充
- 4工控安全工具集
- 5java并发编程的艺术和并发编程这一篇就够了_java并发编程的艺术和java并发编程之美
- 6语义分割综述_语义分割多通道数据
- 7寒假集训一期总结
- 8MySQL的四个事务隔离级别有哪些?各自存在哪些问题?_mysql事物的隔离级别
- 9LangChain曝关键漏洞,数百万AI应用面临攻击风险_langchain 漏洞
- 10[转](21条消息) Pico Neo 3教程☀️ 三、SDK 的进阶功能_pico3怎么转换场景
机器学习(西瓜书)学习笔记3——模型评估与选择_traing error
赞
踩
一、经验误差和过拟合
1.经验误差:学习器在训练集上的误差称为“训练误差”(traing error)或“经验误差”(empirical error)。
2.泛化误差:学习器在新样本上的误差称为泛化误差(generalization error)。
泛化误差小的学习器是我们想要的。
3、过拟合:当学习器把训练样本学的太好,很可能把训练数据的特征作为所有数据都具有的特征,这样会导致学习器在测试集上效果变差,泛化性能下降,这种现象叫做过拟合(overfitting)。过拟合无法避免,只能缓解算法中的过拟合。
4、欠拟合:由于学习器的学习能力太弱,然后数据复杂度较高,使得学习器没有学到数据的一般特征,导致学习器泛化能力减弱。
二、评估方法
1.留出法:直接将数据D分为两个互斥的集合,其中一个集合作为训练集S,另一个作为测试集T。
留出法在对数据进行划分时要保持数据分布一致,避免因数据划分过程引入额外的偏差对最终结果造成影响。常见的做法是将2/3~4/5的样本用于训练,剩余样本用于测试。
2.交叉验证:先将数据集D划分为k个大小相似的互斥子集,每个子集 都尽可能保持数据分布一致,然后,每次用k-1个子集的并集作为训练集,余下的那个子集作为测试集。这样可以得到k组训练/测试集,从而进行k次训练和测试,最终返回这k个测试结果的均值。交叉验证法评估结果的稳定性和保真性由k值决定。为了强调这一点,交叉验证也称为k折交叉验证,k通常取值为10,此时称为十折交叉验证。
都尽可能保持数据分布一致,然后,每次用k-1个子集的并集作为训练集,余下的那个子集作为测试集。这样可以得到k组训练/测试集,从而进行k次训练和测试,最终返回这k个测试结果的均值。交叉验证法评估结果的稳定性和保真性由k值决定。为了强调这一点,交叉验证也称为k折交叉验证,k通常取值为10,此时称为十折交叉验证。
由于留出法和交叉验证法保留了一部分样本用于测试,因此实际评估的模型所使用的训练集比D小,这必然会引入一些因训练样本规模不同而导致的估计偏差。基于以上分析,我们有自助法解决以下问题。
3.自助法:给定包含m个样本的数据集D,每次从数据集D中随机抽取一个样本放入数据集D'中,然后再将此样本放入D中。将此过程重复m次,得到含有m个样本的数据集D',这就是自主抽样的结果。显然,D中有一部分样本会在D'中重复出现,而另一部分样本不出现。样本在m次采样中始终不被采到的概率是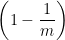 ,取极限得:
,取极限得:
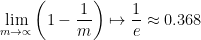
由此可知,数据集D中有36.8%的数据未出现在采样数据集D'中。于是可将D'作为训练集,D\D'作为测试集。自助法在数据集小,难以有效划分训练集和测试集时很有用,这对集成学习等方法有很大的好处。然而,自助法产生的数据集改变了初始数据集的分布,这会引入估计偏差。因此,在数据量足够时,留出法和交叉验证更常用。
三、性能度量
1.均方误差:在预测任务中,给定样例集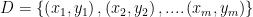 ,其中,
,其中, 是
是 的真实标记。要评估学习器的性能,就要把学习器的预测结果
的真实标记。要评估学习器的性能,就要把学习器的预测结果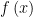 与真实标记
与真实标记 进行比较。
进行比较。
回归任务最常用的性能度量是“均方误差”(mean squared error):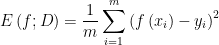
2、查准率、查全率
查准率:学习器在测试过程找出的数据中正确的比率。
查全率:学习器在测试过程中找出的数据占总测试数据的比率。
对于二分类问题,可将样例根据其真实类别与学习器预测类别的组合划分为真正例(true positive,TP)、假正例(false positive,FP)、真反例(true negative,TN)、假反例(false negative,FN)。TP+FP+TN+FN=样例总数。
分类结果的混淆矩阵如下表所示:
| 真实情况 | 预测结果 | |
| 正例 | 反例 | |
| 正例 | TP | FN |
| 反例 | FP | TN |
查准率的计算公式: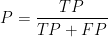 。查全率的计算公式:
。查全率的计算公式: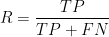
查准率和查全率是相互矛盾的,“你高我低”,如果尽可能选对好瓜,那肯定只挑选出了最有把握的瓜,这导致查准率高、查全率低。如果尽可能把好瓜都挑出来,那么所有好瓜必然都选上了,这样查全率就高,但是查准率就低了。
3、P-R曲线
将学习器的预测结果进行排序,按照可能性大到可能性小进行排序,每次可以计算出当前的查全率和查准率,以查准率为纵轴、查全率为横轴作图,就得到了P-R曲线。如果一个学习器A的P-R曲线在学习器B的PR曲线之上,那么,学习器A的性能优于学习器B的性能。
4、ROC和AUC
ROC(Receiver Operation Characteristic):我们根据学习器的预测结果对样例进行排序,按此顺序逐个把样本作为正例进行预测,每次计算出真正例率(True Positive Rate,TPR)和假正例率(False Positive Rate,TPR),分别以他们为横(假正例率)、纵(真正例率)坐标作图,从而得ROC曲线。
真正例率: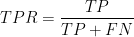 假正例率:
假正例率: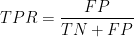
AUC(Area Under ROC Curve)ROC曲线与横纵坐标轴围成的区域称为AUC


