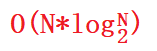C语言（插入、选择、冒泡、快速）排序_c语言插入算法的动图

目录

 

前言

一、插入排序

二.选择排序

三.冒泡排序

四、快速排序

hoare版本(左右指针法)

时间复杂度、稳定性表

---

 

前言

这里实现几种常见的排序算法：

一、插入排序

1.1直接插入

把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列

步骤：

1.从第一个元素开始，该元素可以认为已经被排序
2.取下一个元素tem，从已排序的元素序列从后往前扫描
3.如果该元素大于tem，则将该元素移到下一位
4.重复步骤3，直到找到已排序元素中小于等于tem的元素
5.tem插入到该元素的后面，如果已排序所有元素都大于tem，则将tem插入到下标为0的位置
6.重复步骤2~5

动图演示如下：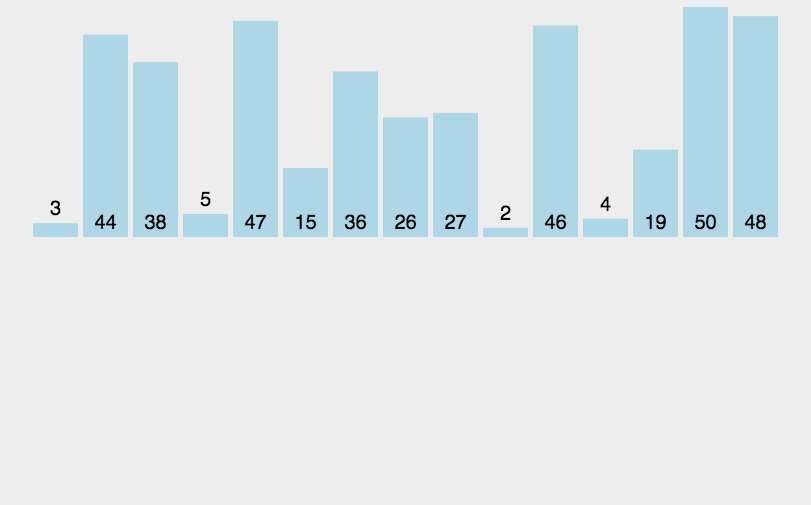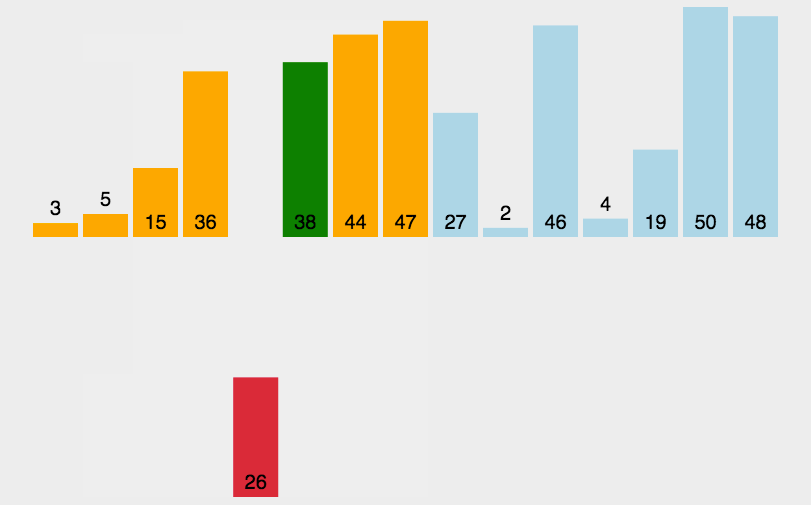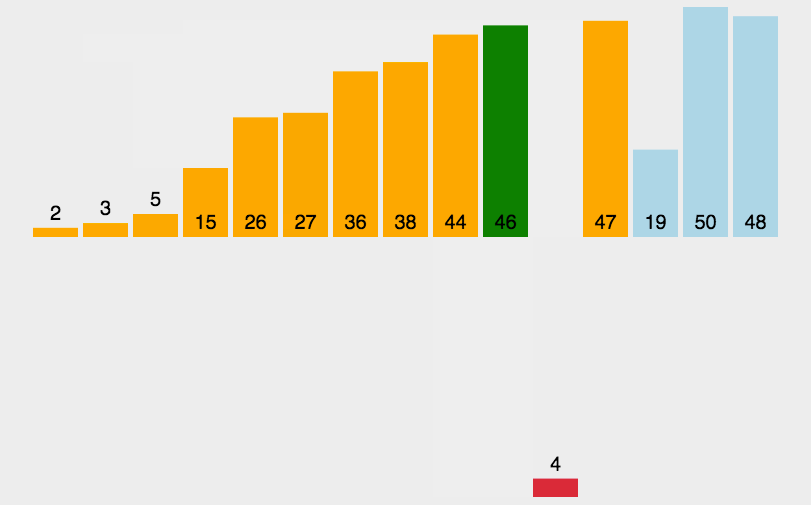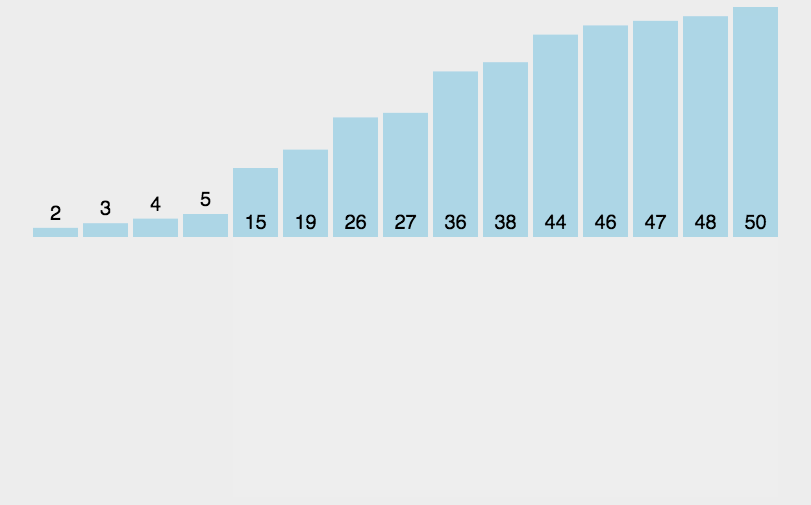

思路：
  在待排序的元素中，假设前n-1个元素已有序，现将第n个元素插入到前面已经排好的序列中，使得前n个元素有序。按照此法对所有元素进行插入，直到整个序列有序。

但我们并不能确定待排元素中究竟哪一部分是有序的，所以我们一开始只能认为第一个元素是有序的，依次将其后面的元素插入到这个有序序列中来，直到整个序列有序为止。 

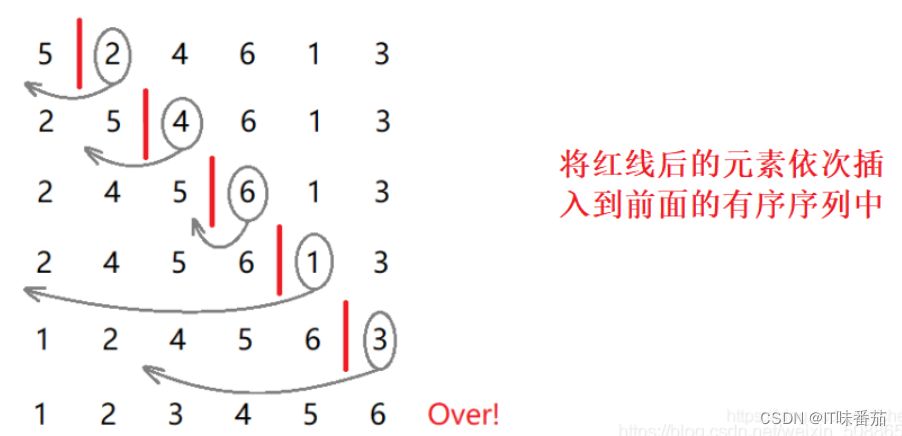
代码如下：

void InsertSort(int* arr, int n)
{
	for(int i=0;i<n-1;i++){
		
		int end = i;
		int temp = arr[i+1];
		
		while(end >= 0){
			if(arr[end] > temp){
				arr[end+1] = arr[end];
				end--;
			}else{
				break;
			}
		}
		
		arr[end+1] = temp;
	}
}

 时间复杂度：最坏情况下为O(N*N)，此时待排序列为逆序，或者说接近逆序
      最好情况下为O(N)，此时待排序列为升序，或者说接近升序。
空间复杂度：O(1)

1.2希尔排序

基本思想：
希尔排序也是插入排序中的一种，因为其本质就是使用了插入排序，我们从插入排序的结论中可以得出，越接近有序的数组使用插入排序的效率越高。希尔排序的思想，就是使一个数组先部分有序，最后在全局有序。那么如何实现部分有序呢，我们可以对数组的元素按照某种规律进行分组，分组后，对组内的记录进行排序，如何重复进行分组和排序，当最终每组的成员只剩一个时，在进行排序的时候，就是使用了插入排序。 

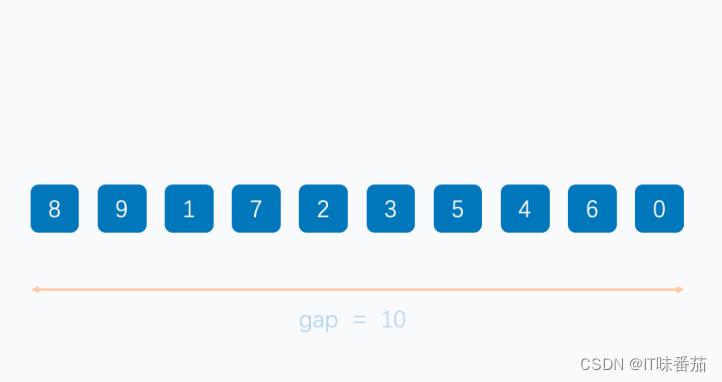
代码实现 

// 希尔排序
void ShellSort(int* a, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;
 
		for (int i = 0; i < n - gap; ++i)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}

我们定义了一个gap变量，这个变量是用来进行分组的，当gap大于1的时候，每次排序其实都是在预排序，也就是对分组内的成员进行排序，gap是间隔，也就是将i，i+gap，i+2*gap...依次进行排序，之后，gap/2或者gap/3+1，按照某种规律，最终gap=1的时候，在进行排序，就是进行了一次直接插入排序。

算法分析 

希尔排序的时间复杂度是一个复杂的问题，在Kunth所著的《计算机程序设计技巧》第3卷中，利用大量的实验统计资料得出，平均复杂度为O(N^1.25)到O(1.6 * N^1.25)。这里的就暂且不讨论该结果具体得出的方式。

希尔排序是否是稳定的算法呢？答案是不稳定的，因为我们在预排序的过程中，我们会进行大量的跳动式的移动元素的值，因此会导致不能按照原先的序列进行排序。

希尔排序中的gap是如何取值的呢？当成Shell，也就是该算法的原作者，提出取gap= gap/2，然后向下取整，直到gap=1时。后来Kunth提出取gap = gap/3 + 1 ，gap/3向下取整的方式，直到gap=1时。这两种方式没有说哪个好，哪个坏，因此，使用其中一个即可。
 

二、选择排序

思路：
每次从待排序列中选出一个最小值，然后放在序列的起始位置，直到全部待排数据排完即可。
实际上，我们可以一趟选出两个值，一个最大值一个最小值，然后将其放在序列开头和末尾，这样可以使选择排序的效率快一倍。

动图如下：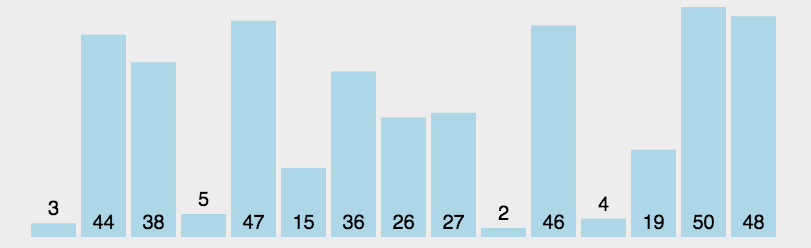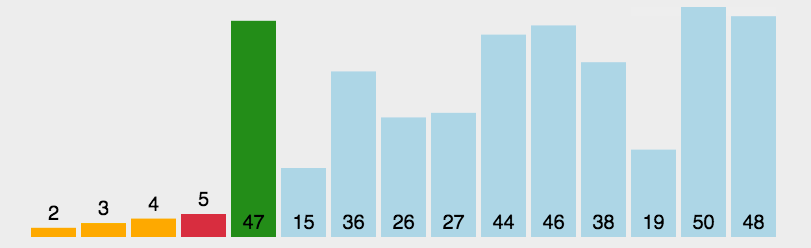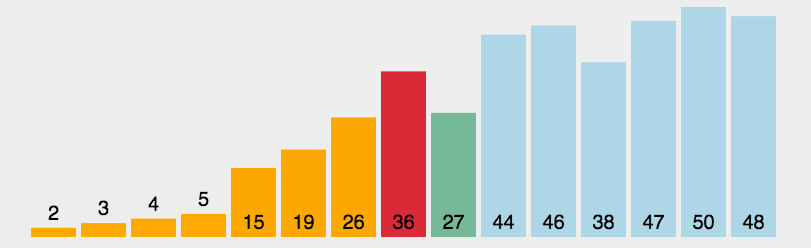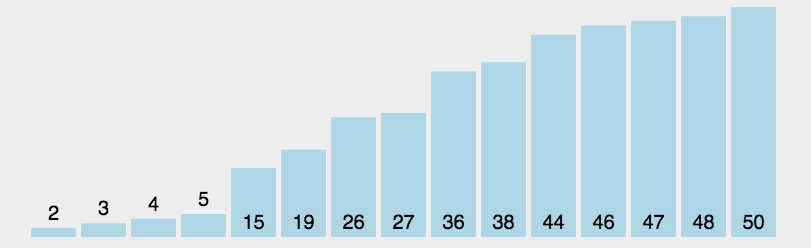

代码如下：

void SelectSort(int* arr, int n)
{
	for(int i=0;i<n-1;i++){
		
		int max = arr[i];
		int tip = 0;
		int j = 0;
		for(j=i+1;j<n;j++){
			if(max < arr[j]){
				max = arr[j];
				tip = j;
			}
		}
		if(max > arr[i]){
			int temp = arr[i];
			arr[i] = max;
			arr[tip] = temp;
		}
	}
}

 时间复杂度：最坏情况：O(N^2)
      最好情况：O(N^2)
空间复杂度：O(1)

三、交换排序

3.1冒泡排序

思路：
左边大于右边交换一趟排下来最大的在右边

动图如下：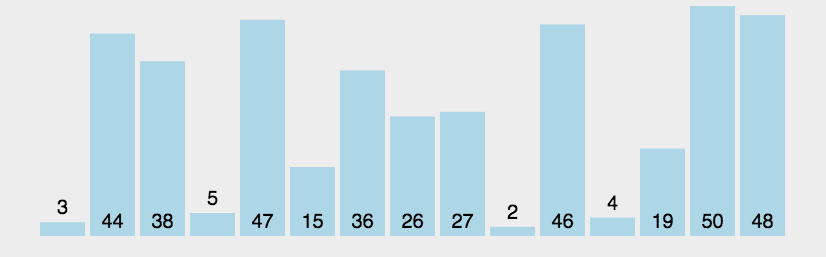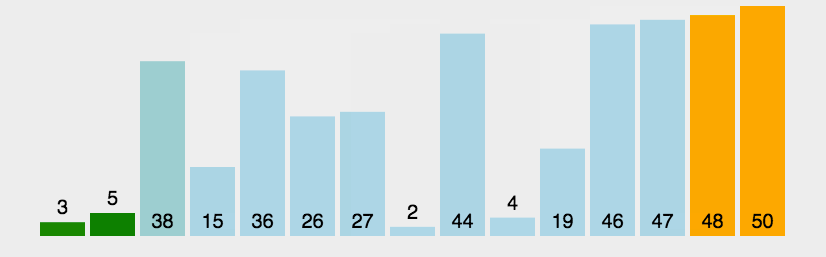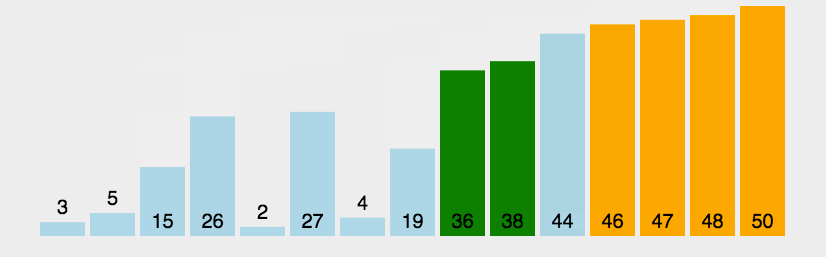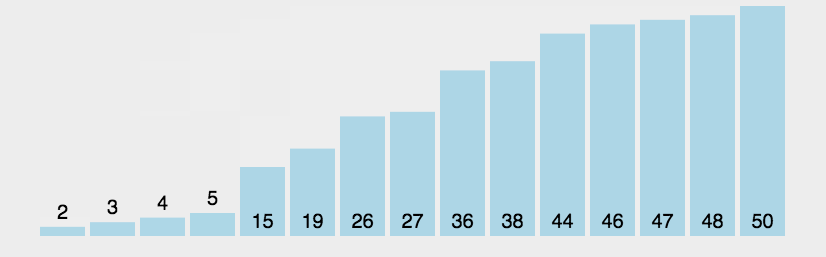

代码如下：

void BubbleSort(int* arr, int n)
{
	for (int i = 0; i < n - 1; i++)
	{
		for (int j = 0; j < n - i -1 ; j++)
		{
			if (arr[j] > arr[j + 1])
			{
				int temp = arr[j + 1];
				arr[j + 1] = arr[j];
				arr[j] = temp;
			}
		}
	}
}

 时间复杂度：最坏情况：O(N^2)
      最好情况：O(N)
空间复杂度：O(1)

3.2、快速排序

hoare版本(左右指针法)

思路：
1、选出一个key，一般是最左边或是最右边的。
2、定义一个begin和一个end，begin从左向右走，end从右向左走。（需要注意的是：若选择最左边的数据作为key，则需要end先走；若选择最右边的数据作为key，则需要bengin先走）。

3、在走的过程中，若end遇到小于key的数，则停下，begin开始走，直到begin遇到一个大于key的数时，将begin和right的内容交换，end再次开始走，如此进行下去，直到begin和end最终相遇，此时将相遇点的内容与key交换即可。（选取最左边的值作为key）
4.此时key的左边都是小于key的数，key的右边都是大于key的数

5.将key的左序列和右序列再次进行这种单趟排序，如此反复操作下去，直到左右序列只有一个数据，或是左右序列不存在时，便停止操作，此时此部分已有序

单趟动图如下：

代码如下：

void swap(int* a, int* b)
{
	int tem = *a;
	*a = *b;
	*b = tem;
}
//快速排序左右指针
void QuickSort(int* arr, int begin, int end)
{
	if(begin >= end){
		return;
	}
	int left = begin;
	int right = end;
	int key = begin;
	
	while(begin < end){
		
		//右边选小  等号防止和key值相等    防止顺序begin和end越界
		while(arr[end] >= arr[key] && begin < end){
			end--;
		}
		//左边选大
		while(arr[begin] <= arr[key] && begin < end){
			begin++;
		}
		//大的换到右边，小的换到左边
		swap(&arr[begin],&arr[end]);
	}
	swap(&arr[key],&arr[end]);
	key = end;
	QuickSort(arr,left,key-1);
	QuickSort(arr,key+1,right);
}
 
int main()
{
	int nums[] = { 3,5,26,2,27,2,46,4,19,50,48 };
	int size = sizeof(nums) / sizeof(nums[0]);
	QuickSort(nums,0, size-1);
	for (int i = 0; i < size; i++)
	{
		printf("%d ", nums[i]);
	}
	return 0;
}

时间复杂度:

四、归并排序

 基本思想 

归并排序是建立在归并操作上的一种有效的排序算法，该算法采用的是分治法。其思想就是将序列分成n个子序列，再使用子序列有序，之后，将其合并为一个新的有序表，如果两个有序表合并为一个有序表，称为二路归并。

 

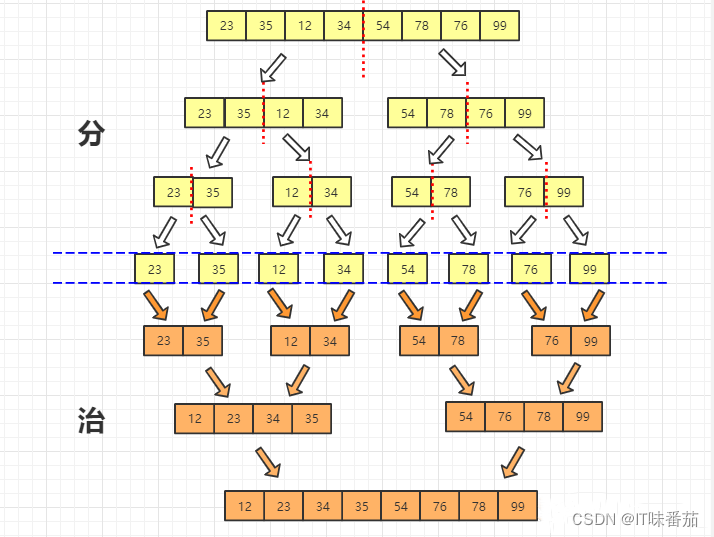
代码实现 

​​​​​​​递归版本：

void _MergeSort(int* a, int begin, int end, int* tmp)
{
	if (begin >= end)
		return;
 
	int mid = (begin + end) / 2;
 
	// [begin, mid] [mid+1, end] 分治递归，让子区间有序
	_MergeSort(a, begin, mid, tmp);
	_MergeSort(a, mid + 1, end, tmp);
 
	//归并 [begin, mid] [mid+1, end]
	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;
	int i = begin1;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}
 
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
 
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}
 
	// 把归并数据拷贝回原数组
	memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
 
void MergeSort(int* a, int n)
{
	// 借助一个新的辅助空间来帮助合并
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
 
	_MergeSort(a, 0, n - 1, tmp);
 
	free(tmp);
}

首先，要知道这个算法的实现，要先要理解分治，分就是将数组分成n个子序列，治就是合并的意思，这里采用的是二路归并排序，将两个子序列进行比较，然后在拷贝为原数组中。最后将同时划分的序列合并。

非递归版本：

非递归实现的思想与递归实现的思想是类似的。

不同的是，这里的序列划分过程和递归是相反的，不是一次一分为二，而是先1个元素一组，再2个元素一组，4个元素一组…直到将所有的元素归并完。

void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
 
	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
 
			// end1越界或者begin2越界，则可以不归并了
			if (end1 >= n || begin2 >= n)
			{
				break;
			}
			else if (end2 >= n)
			{
				end2 = n - 1;
			}
 
			int m = end2 - begin1 + 1;
			int j = begin1;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}
 
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
 
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
 
			memcpy(a + i, tmp + i, sizeof(int) * m);
		}
 
		gap *= 2;
	}
 
	free(tmp);
}

时间复杂度、稳定性表

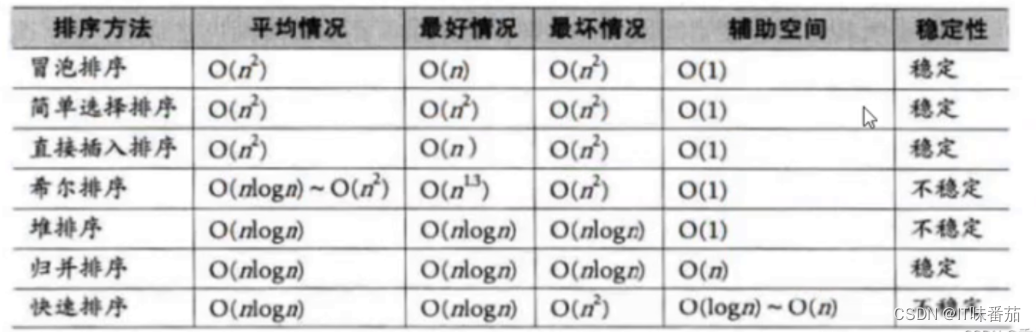
稳定性： 是指数组中相同的值，排完序以后，相对顺序不变，就是稳定的，否则就是不稳定的