【代码随想录】【算法训练营】【第39天】 [62]不同路径 [63]不同路径II [343]整数拆分 [96]不同的二叉搜索树

前言

思路及算法思维，指路 代码随想录。
题目来自 LeetCode。

day 39，周六，坚持不住了~

题目详情

[62] 不同路径

题目描述

62 不同路径

解题思路

前提：每次只能向下或者向右移动一步
思路：动态规划， dp[i][j]: 到达(i, j)位置的路径数量， dp[i][j] = dp[i-1][j] + dp[i][j-1] 。
重点：dp数组的定义，以及 推导公式。

代码实现

C语言

动态规划dp[i][j]

动态规划 dp[i][j]: 到达(i, j)位置的路径数量, dp[i][j] = dp[i-1][j] + dp[i][j-1];

// dp[i][j]: 到达(i, j)位置的路径数量, dp[i][j] = dp[i-1][j] + dp[i][j-1];
int uniquePaths(int m, int n) {
    int dp[m][n];
    // 动态数组初始化
    for (int i = 0; i < m; i++) {
        dp[i][0] = 1;
    }
    for (int j = 0; j < n; j++) {
        dp[0][j] = 1;
    }
    // 从前到后，遍历其余位置
    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        }
    }
    return dp[m - 1][n - 1];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

动态规划dp[i]

动态规划 dp[i][j]压缩空间为dp[i], dp[i] = dp[i] + dp[i-1]

// dp[i][j]: 到达(i, j)位置的路径数量, dp[i][j] = dp[i-1][j] + dp[i][j-1];
// 压缩空间为dp[i], dp[i] = dp[i] + dp[i-1]
int uniquePaths(int m, int n) {
    int dp[n];
    // 动态数组初始化
    for (int j = 0; j < n; j++) {
        dp[j] = 1;
    }
    // 从前到后，按行更新数组
    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            dp[j] = dp[j - 1] + dp[j];
        }
    }
    return dp[n - 1];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

[63] 不同路径II

题目描述

63 不同路径II

解题思路

前提：每次只能向下或者向右移动一步，且可能有障碍
思路：动态规划：d[i][j]: 到达(i, j)位置的路径数量, dp[i][j] = dp[i-1][j] + dp[i][j-1] 。
重点：dp数组的定义，以及 推导公式。

代码实现

C语言

动态规划dp[i][j]

动态规划：d[i][j]: 到达(i, j)位置的路径数量, dp[i][j] = dp[i-1][j] + dp[i][j-1]

// d[i][j]: 到达(i, j)位置的路径数量, dp[i][j] = dp[i-1][j] + dp[i][j-1]
int uniquePathsWithObstacles(int** obstacleGrid, int obstacleGridSize, int* obstacleGridColSize) {
    //定义dp数组
    int dp[obstacleGridSize][*obstacleGridColSize];
    //初始化dp数组
    int found = false;
    for (int i = 0; i < obstacleGridSize; i++) {
        if ((found != true) && (obstacleGrid[i][0] != 1)) {
            dp[i][0] = 1;
        } else {
            found = true;
            dp[i][0] = 0;
        }
        
    }
    found = false;
    for (int j = 0; j < *obstacleGridColSize; j++) {
        if ((found != true) && (obstacleGrid[0][j] != 1)) {
            dp[0][j] = 1;
        } else {
            found = true;
            dp[0][j] = 0;
        }
    }
    // 从上到下，从左到右，遍历
    for (int i = 1; i < obstacleGridSize; i++) {
        for (int j = 1; j < *obstacleGridColSize; j++) {
            // 判断是否为障碍
            if (obstacleGrid[i][j] != 1) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            } else {
                dp[i][j] = 0;
            }
        } 
    }
    return dp[obstacleGridSize - 1][*obstacleGridColSize - 1];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

动态规划dp[i]

d[i][j]压缩为d[i], dp[i] = dp[i-1] + dp[i]

// d[i][j]: 到达(i, j)位置的路径数量, dp[i][j] = dp[i-1][j] + dp[i][j-1]
// 压缩为d[i], dp[i] = dp[i-1] + dp[i]
int uniquePathsWithObstacles(int** obstacleGrid, int obstacleGridSize, int* obstacleGridColSize) {
    //定义dp数组
    int dp[*obstacleGridColSize];
    //初始化dp数组
    int found = false;
    for (int j = 0; j < *obstacleGridColSize; j++) {
        if ((found != true) && (obstacleGrid[0][j] != 1)) {
            dp[j] = 1;
        } else {
            found = true;
            dp[j] = 0;
        }
    }
    // 从上到下，从左到右，遍历
    for (int i = 1; i < obstacleGridSize; i++) {
        for (int j = 0; j < *obstacleGridColSize; j++) {
            // 判断是否为障碍
            if (obstacleGrid[i][j] == 1) {
                dp[j] = 0;
            } else if (j > 0) {
                dp[j] = dp[j - 1] + dp[j];
            }
        } 
    }
    return dp[*obstacleGridColSize - 1];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

[343] 整数拆分

题目描述

343 整数拆分

解题思路

前提：拆分为 k 个 正整数 的和（ k >= 2 ）
思路：动态规划， dp[i]: i的最大乘积, 拆分为两数或者多数之积, d[i] = max(j*(i-j), jdp[i-j]); 遍历j时, 取各个dp[i]的最大值, 故dp[i] = max(dp[i], j(i-j), j*dp[i-j])。
重点：dp数组的定义，以及 推导公式。

代码实现

C语言

动态规划

// dp[i]: i的最大乘积, 拆分为两数或者多数之积, d[i] = max(j*(i-j), j*dp[i-j])
// 遍历j时, 取各个dp[i]的最大值
// 故dp[i] = max(dp[i], j*(i-j), j*dp[i-j])

int max(int p1, int p2)
{
    return p1 > p2 ? p1 : p2;
}

int integerBreak(int n) {
    // 定义dp数组
    int dp[n + 1];
    // 初始化
    for (int i = 0; i < (n + 1); i++) {
        dp[i] = 0;
    }
    dp[1] = 1;
    // 从小到大遍历整数
    for (int i = 2; i <= n; i++) {
        for (int j = 1; j < i; j++) {
            dp[i] = max(dp[i], max((j * dp[i - j]), j * (i - j)));
        }
    }
    return dp[n];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

动态规划 优化遍历

// dp[i]: i的最大乘积, 拆分为两数或者多数之积, d[i] = max(j*(i-j), j*dp[i-j])
// 遍历j时, 取各个dp[i]的最大值
// 故dp[i] = max(dp[i], j*(i-j), j*dp[i-j])

int max(int p1, int p2)
{
    return p1 > p2 ? p1 : p2;
}

int integerBreak(int n) {
    // 定义dp数组
    int dp[n + 1];
    // 初始化
    for (int i = 0; i < (n + 1); i++) {
        dp[i] = 0;
    }
    dp[1] = 1;
    // 从小到大遍历整数
    for (int i = 2; i <= n; i++) {
        // 优化遍历
        for (int j = 1; j <= i / 2; j++) {
            dp[i] = max(dp[i], max((j * dp[i - j]), j * (i - j)));
        }
    }
    return dp[n];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

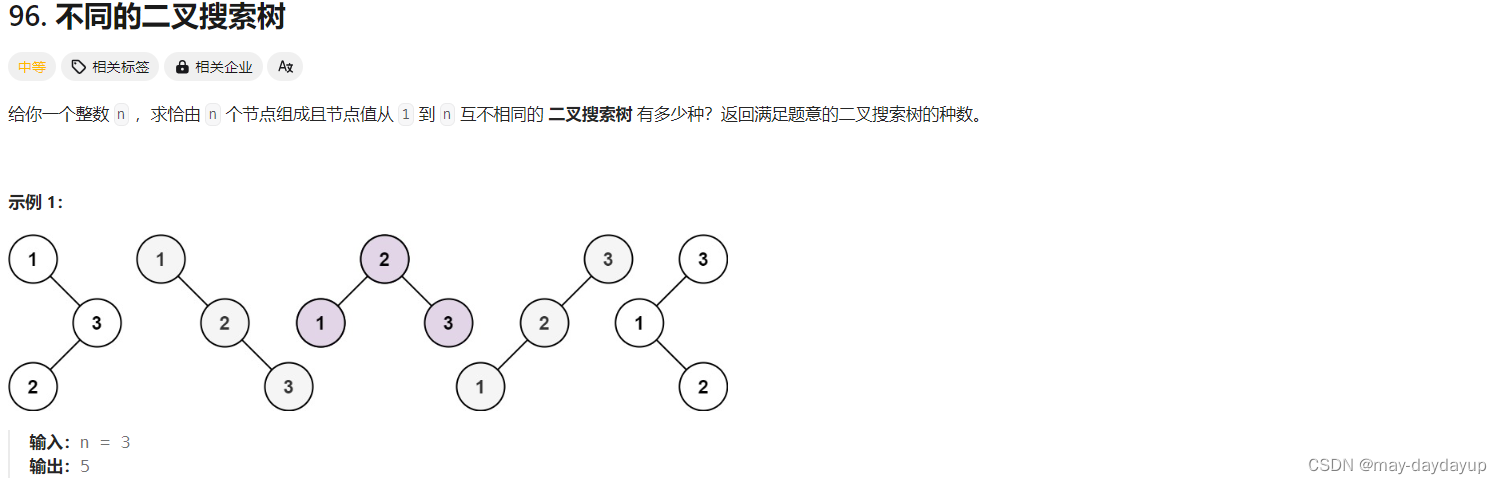
[96] 不同的二叉搜索树

题目描述

96 不同的二叉搜索树

解题思路

前提：查分二叉树的形态，观察联系
思路：动态规划， dp[i]表示i个结点的二叉搜索树的种数, dp[i] += dp[j] * dp[i - j - 1]，其中左子树结点数为j, 右子树结点数为i-j-1。
重点：观察二叉树结点数量之间形态的联系，dp数组的定义，以及 推导公式。

代码实现

C语言

动态规划

// dp[i]表示i个结点的二叉搜索树的种数, dp[i] += dp[j] * dp[i - j - 1]
// 左子树结点数为j, 右子树结点数为i-j-1
int numTrees(int n) {
    // 定义dp数组
    int dp[n + 1];
    // 初始化
    for (int i = 0; i <= n; i++) {
        dp[i] = 0;
    }
    dp[0] = 1;
    // 从小到大遍历n
    for (int i = 1; i <= n; i++) {
        for (int j = 0; j < i; j++) {
            dp[i] += dp[j] * dp[i - j - 1];
        }
    }
    return dp[n];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

今日收获

1. 动态规划五步曲：确定dp数组（dp table）以及下标的含义；确定递推公式；dp数组如何初始化；确定遍历顺序；举例推导dp数组。