红黑树结构_红黑树如何构造出来

更多内容，前往 IT-BLOG

AVL （平衡二叉树：追求"完全平衡"）树的另一种变种是红黑树（Red-Black-Tree：只要求部分达到平衡）其就是一个二叉查找树。对红黑树的操作在最坏情形下花费 时间。红黑树是具有下列着色性质的二叉查找树：
【1】每个节点或者是黑色，或者是红色。
【2】根是黑色的；
【3】每个叶子节点（NIL）是黑色。 [注意：这里叶子节点，是指为空(NIL或NULL)的叶子节点！]；
【4】如果一个节点是红色的，则它的子节点必须是黑色的；
【5】从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点；
 

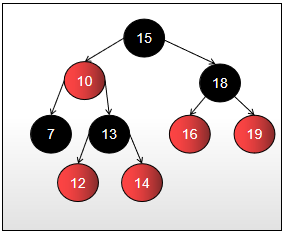
有了上面的几个性质作为限制，即可避免二叉查找树退化成单链表的情况。但是，仅仅避免这种情况还不够，这里还要考虑某个节点到其每个叶子节点路径长度的问题。如果某些路径长度过长，那么，在对这些路径上的结点进行增删查操作时，效率也会大大降低。这个时候性质3和性质4用途就凸显了，有了这两个性质作为约束，即可保证任意节点到其每个叶子节点路径最长不会超过最短路径的2倍。红黑树法则的一个结论是，红黑树的高度最多是2log(N+1)，因此查找操作保证是一种对树的操作。和往常一样，困难在于将一个新节点插入到树中。如何继续维持树的平衡，通常使用改变树的颜色和树的旋转。默认插入的节点都为红色，不然就会失衡。下面我们就看个例子

一、基本概念

---

左旋（盗取网上一张动图如下）以父节点 E 为旋转点，将 S 左旋为 E 的父节点，同时将 S 的左子树修改为 E 的右子树。右旋是怎样的呢？不就是左旋的结果，又给还原回去的样子么。哈哈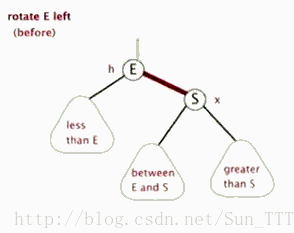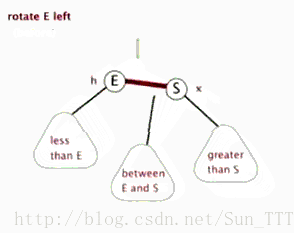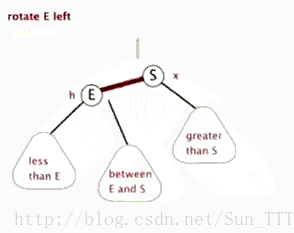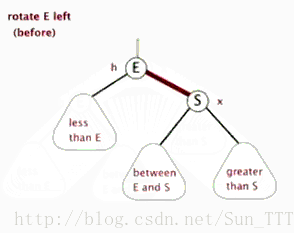

二、红黑树的添加操作流程

---

【第一步】：将红黑树当作一颗二叉查找树，将节点插入。红黑树本身就是一颗二叉查找树，将节点插入后，该树仍然是一颗二叉查找树。也就意味着，树的键值仍然是有序的。此外，无论是左旋还是右旋，若旋转之前这棵树是二叉查找树，旋转之后它一定还是二叉查找树。这也就意味着，任何的旋转和重新着色操作，都不会改变它仍然是一颗二叉查找树的事实。
【第二步】：将插入的节点着色为"红色"。为什么着色成红色，而不是黑色呢？为什么呢？在回答之前，我们需要重新温习一下红黑树的特性：将插入的节点着色为红色，不会违背"特性(5)"！少违背一条特性，就意味着我们需要处理的情况越少。接下来，就要努力的让这棵树满足其它性质即可；满足了的话，它就又是一颗红黑树了。
【第三步】：通过一系列的旋转或着色等操作，使之重新成为一颗红黑树。第二步中，将插入节点着色为"红色"之后，不会违背"特性(5)"。那它到底会违背哪些特性呢？
【1】对于"特性(1)"，显然不会违背了。因为我们已经将它涂成红色了。
【2】对于"特性(2)"，显然也不会违背。在第一步中，我们是将红黑树当作二叉查找树，然后执行的插入操作。而根据二叉查找数的特点，插入操作不会改变根节点。所以，根节点仍然是黑色。
【3】对于"特性(3)"，显然不会违背了。这里的叶子节点是指的空叶子节点，插入非空节点并不会对它们造成影响。
【4】对于"特性(4)"，是有可能违背的！那接下来，想办法使之"满足特性(4)"，就可以将树重新构造成红黑树了。

三、红黑树插入案例演示

---

【1】改变颜色：最简单，红变黑、黑边红（场景描述：当前节点<11节点>为红色，父节点<12节点>也为红色，叔叔节点<14节点>也是红色此种情况就采用变颜色的方式。将父节点、叔叔节点设置为黑色；爷爷节点变为红色）；举个栗子：如下我们插入了一个节点<11节点>（图一），符合我们上面描述的场景，对其进行变色。变色后为图二，但存在两个连续的红色节点，此时不符合变色规则，就需要采用左旋转。

【2】左旋：当前节点<10节点>为红色，父节点<13节点>为红色，叔叔节点<14节点>为黑色，且当前节点是右子树时。左旋以父节点作为左旋。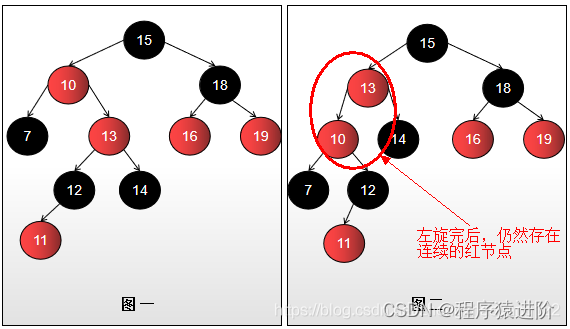

【3】右旋：当前节点为红色，父节点<13节点>为红色，叔叔节点<18节点>为黑色，且当前节点是左子树时。右旋（① 将父节点<13节点>变为黑色；② 爷爷节点<15节点>变为红色；③ 爷爷节点<15节点>旋转）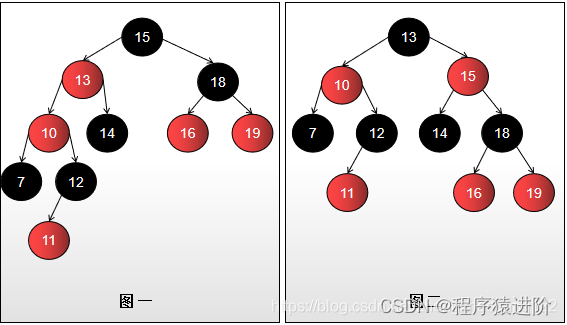

四、红黑树代码演示

---

红黑树的应用比较广泛，主要是用它来存储有序的数据，它的时间复杂度是O(lgn)，效率非常之高。例如，Java集合中的 TreeSet和 TreeMap；

/**
 * 红黑树的插入和左旋方法
 */
public class RedBlackTree {
 
    //定义两种颜色
    private final String R = "red";    //红
    private final String B = "black";  //黑
    //定义一个 Root 节点
    private Node root = null;
 
    //创建一个 Node 节点对象
    class Node{
        private int data; //数据
        private String color = R; //颜色
        private Node right;  //右子树
        private Node left;   //左子树
        private Node parent; //父节点
 
        //构造器,创建节点的时候需要出入数据即可(父节点)
        public Node(int data){
            this.data = data;
        }
    }
 
    //插入方法
    public void insert(Node node, int data){
        //插入的大，说明插入到右子树
        if(node.data < data){
            //如果为空则直接插入
            if(node.right == null){
                node.right = new Node(data);
            }else{
                //递归调用 insert ****************
                insert(node.right,data);
            }
        //否则插入到左子树
        }else{
            node.left = new Node(data);
            //如果为空则直接插入
            if(node.left == null){
                node.left = new Node(data);
            }else{
                //递归调用 insert
                insert(node.left,data);
            }
        }
    }
 
    //左旋规则:按照动图的规则来写
    public void leftRotate(Node node){
        //根节点
        if(node.parent == null){
            Node E = root;
            Node S = E.right;
 
            //第一步 将E 的父节点赋值为S
            E.parent = S;
            //第二步 将E 的右节点赋值为S的左节点
            E.right = S.left;
            //第三步 将S 的左节点赋值为 E
            S.left = E;
            //S 的parent 赋值为 null
            S.parent = null;
        }
    }
}

五、红黑树的结点删除操作

---

将红黑树内的某一个节点删除。需要执行的操作依次是：首先，将红黑树当作一颗二叉查找树，将该节点从二叉查找树中删除；然后，通过"旋转和重新着色"等一系列来修正该树，使之重新成为一棵红黑树。详细描述如下：
【第一步】：将红黑树当作一颗二叉查找树，将节点删除。这和"删除常规二叉查找树中删除节点的方法是一样的"。分3种情况：
【1】被删除节点没有儿子，即为叶节点。那么，直接将该节点删除就OK了。
【2】被删除节点只有一个儿子。那么，直接删除该节点，并用该节点的唯一子节点顶替它的位置。
【3】被删除节点有两个儿子。那么，先找出它的后继节点；然后把“它的后继节点的内容”复制给“该节点的内容”；之后，删除“它的后继节点”。
【第二步】：通过"旋转和重新着色"等一系列来修正该树，使之重新成为一棵红黑树。因为"第一步"中删除节点之后，可能会违背红黑树的特性。所以需要通过"旋转和重新着色"来修正该树，使之重新成为一棵红黑树。

总结

---

作为平衡二叉查找树里面众多的实现之一，红黑树无疑是最简洁、实现最为简单的。红黑树通过引入颜色的概念，通过颜色这个约束条件的使用来保持树的高度平衡。作为平衡二叉查找树，旋转是一个必不可少的操作。通过旋转可以降低树的高度，在红黑树里面还可以转换颜色。

红黑树里面的插入和删除的操作比较难理解，这时要注意记住一点：操作之前红黑树是平衡的，颜色是符合定义的。在操作的时候就需要向兄弟节点、父节点、侄子节点借调和互换颜色，要达到这个目的，就需要不断的进行旋转。所以红黑树的插入删除操作需要不停的旋转，一旦借调了别的节点，删除和插入的节点就会达到局部的平衡（局部符合红黑树的定义），但是被借调的节点就不会平衡了，这时就需要以被借调的节点为起点继续进行调整，直到整棵树都是平衡的。在整个修复的过程中，插入具体的分为3种情况，删除分为4种情况。

整个红黑树的查找，插入和删除都是O(logN)的，原因就是整个红黑树的高度是logN，查找从根到叶，走过的路径是树的高度，删除和插入操作是从叶到根的，所以经过的路径都是logN。