devbox
酷酷是懒虫
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

Python - 深夜数据结构与算法之 Stack & Queue_python 栈 队列

作者：酷酷是懒虫 | 2024-07-15 13:32:12

赞

踩

python 栈 队列

目录

一.引言

二.栈与队列介绍

1.Stack 栈

2.Queue 队列

3.DeQueue 双端队列

4.Stack、Queue 实现

三.经典算法实战

1.Valid-Parentheses [20]

2.Trapping-Water [42]

3.largest-Rectangle-Area [84]

4.Min-Stack [155]

5.Max-Sliding-Window [239]

6.MyCircularDeque [641]

四.总结

一.引言

本文介绍 Python 中的 Stack & Queue，其分别代表栈和队列，虽然有各自的特点，但很多时候 Stack 和 Queue 都可以用 List 来实现，下面我们简单学习下二者的概念并配合一些经典的算法实现加深印象。

二.栈与队列介绍

1.Stack 栈

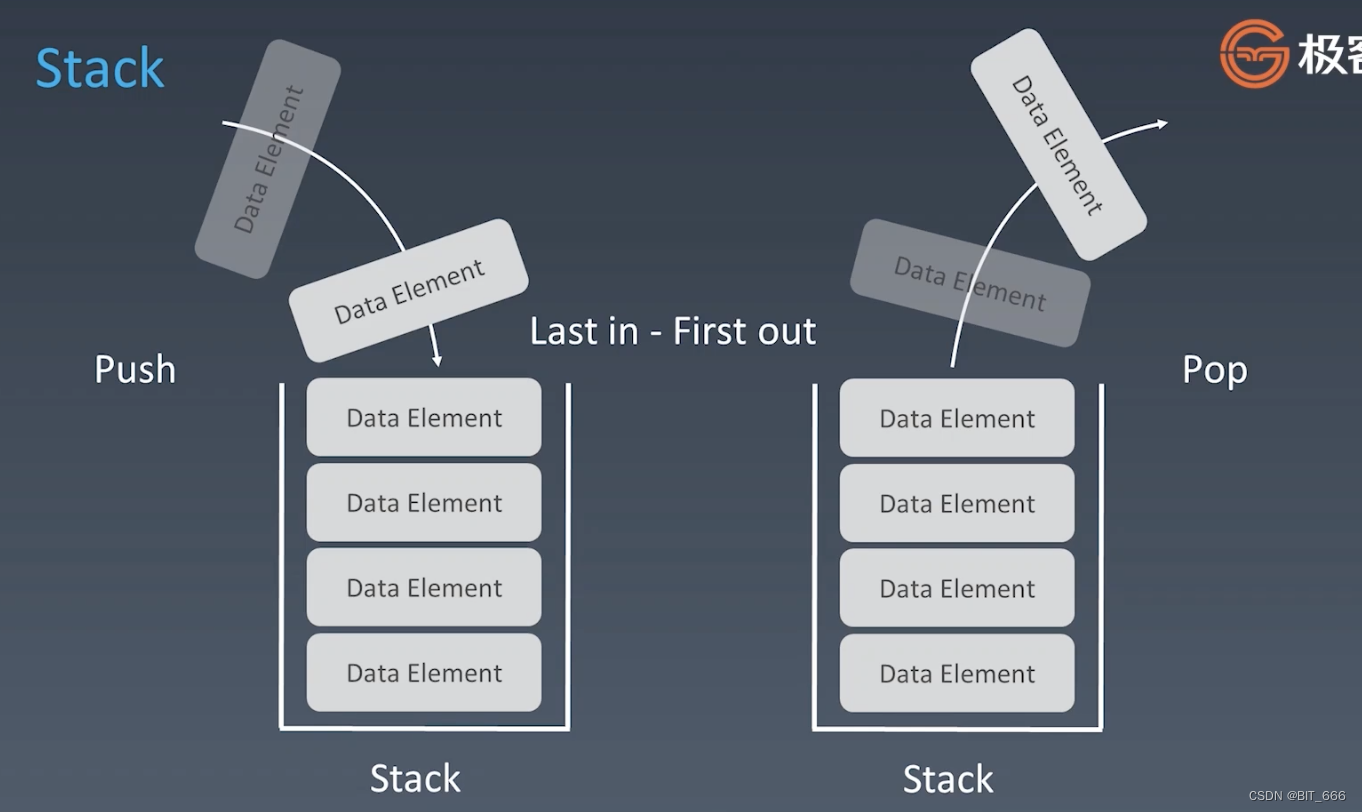
Stack 是一种先进后出的数据结构，即 Last in First out，通常情况下通过 push 或者 offer 将数据压入栈，通过 pop 弹出栈顶元素并返回。其添加和删除节点的时间复杂度均为 O(1)，但是查找一个元素的时间复杂度是 O(n)，因为我们需要遍历整个栈结构才能找到这个元素。生活中栈的应用有很多，我们每天都用的垃圾桶就和栈在结构上就很像，我们先扔进去的垃圾在最底下，最晚扔进去的垃圾在最上面。

2.Queue 队列

队列是一种先进先出的数据结构，即 Last in Last out、First in First out，通常可以通过 push 向队列尾部添加元素，通过 pop 获取队首元素，和 Stack 一样，其添加和删除节点的时间复杂度均为 O(1)，但是查找一个元素的时间复杂度为 O(n)。为了优化查找元素的时间，还有一类数据结构名为优先队列即 Priority Queue，其通过优化底层数据结构将查询的时间优化为 O(logN):

对于队列而言，其最常见的应用场景就是排队了，先到先得，而优先队列也很好理解，队伍里有 VIP 用户，对于 VIP 用户，需要按照其优先级优先出队。

3.DeQueue 双端队列

基于队列 Queue 的概念，后续还提出了 Double-End Queue 即双端队列，顾名思义，它的两端都支持 Push 和 Pop 操作，即两端都可以进出。其和队列 Queue 一样，插入和删除元素时间复杂度都是 O(1)，查找元素是 O(n)。

4.Stack、Queue 实现

Stack 和 Queue 都可以用 List[] 实现，Stack 栈使用 push 向栈内添加元素，使用 pop 返回栈顶元素；Queue 通过 enqueue 实现入队操作，通过 pop(index) 实现出队操作。下面给出数组类数据结构的时间复杂度:

 数据来源: https://www.bigocheatsheet.com/

三.经典算法实战

上面介绍了 Stack、Queue 和 DeQueue 几种数据结构，下面挑选一些 LeetCode 上比较经典的算法，加深对这些数据结构的印象和使用技巧。这里约定一下每个算法的表现形式，Trapping-Water 代表算法名称，[x] 中括号里的 x 代表其对应 LeetCode 的第几题。

1.Valid-Parentheses [20]

有效括号: https://leetcode.cn/problems/valid-parentheses

◆ 题目分析

题目要求匹配括号字符串，其可以使 "[](){}" 这样，也可以是 "((()))" 这样。我们需要做的就是匹配每个左右括号，其满足新进后出的规律，对于 "[](){}" 比较简单，'[' 先进，遇到 ']' 再出，依次匹配即可；对于 "({[]})" 我们先将 "({[" 依次压入栈，随后等待 "]})" 依次匹配它们并 pop 带走，可以看到最左侧的 '(' 是最先进栈的，而它是最后等到 ')' 来匹配，所以最后一个出，非常典型的先进后出。

◆ 触底反弹

  1. #!/usr/bin/python
  2. # -*- coding: UTF-8 -*-
  3.  
  4. class Solution(object):
  5.     def isValid(self, s):
  6.         """
  7.         :type s: str
  8.         :rtype: bool
  9.         """
  10.  
  11.         # 奇数个 char 肯定不对
  12.         if len(s) % 2 != 0:
  13.             return False
  14.  
  15.         # 括号对应关系
  16.         m = {"(": ")", "{": "}", "[": "]"}
  17.  
  18.         # 记录括号的栈
  19.         stack = []
  20.  
  21.         for char in s:
  22.             # 左括号压入栈
  23.             if char in m.keys():
  24.                 stack.append(m[char])
  25.             elif char in m.values():
  26.                 # 右括号到栈里找括号，找不到或找错说明不匹配
  27.                 if stack == [] or char != stack.pop():
  28.                     return False
  29.             else:
  30.                 # 特殊情况，防止异常的字符
  31.                 return False
  32.         # 括号数量不匹配 or 数量为偶数
  33.         return stack == []
'
运行

由于题目只规定了字符串有 3 种类型，所以我们预先构造了左右括号的映射用于判断二者是否匹配。最开始判断字符串为奇数直接退出，因为奇数个括号肯定匹配不完。剩下遇到左括号就进栈右括号，遇到右括号就 pop 匹配，只要二者不相等就退出 False。

◆ 二刷留念

  1. class Solution(object):
  2.     def isValid(self, s):
  3.         """
  4.         :type s: str
  5.         :rtype: bool
  6.         """
  7.  
  8.         # 奇数直接返回
  9.         if len(s) % 2 != 0:
  10.             return False
  11.  
  12.         m = {"(": ")", "{": "}", "[": "]"}
  13.  
  14.         stack = []
  15.  
  16.         # 判断 stack 是否为空
  17.         for char in s:
  18.             if char in m:
  19.                 stack.append(m[char])
  20.             elif not stack or char != stack.pop():
  21.                 return False
  22.         
  23.         return not stack
'
运行

优化了 is else 的判断逻辑，更加简洁。

2.Trapping-Water [42]

接雨水: https://leetcode.cn/problems/trapping-rain-water

◆ 题目分析

通过非负整数数组代表柱子高度，柱子凹槽的部门可以接雨水，求接水的量其实就是求凹槽的总面积。这一题和下面的求柱子最大矩形面积比较类似，根据木桶效应，能接到雨水需要中间的柱子低，两边的柱子比中间柱子高即可。

所以针对我们每一根内部即中间的柱子，我们只需要找其左侧和右侧的最高柱就能计算其接水面积，min(left_max - right_max) 代表当前桶的高度，cur_heigth 代表桶底多高，二者相减即为雨水量，如果前面小于等于后面那么相减会得到非正整数，那就就接不到雨水了，反之高度差多少就能接多少，遍历完内部的柱子 1: len-1，雨水总面积也就求出来了。这道题目是面试的经典题目，其内部的思想其实也很很多题目相同，下面实践一下。 

◆ 暴力开工

  1. class Solution(object):
  2.     def trap(self, height):
  3.         res = 0
  4.         
  5.         for i in range(len(height)):
  6.             # 左右两根柱子无法计算
  7.             if i == 0 or i == len(height) - 1: continue
  8.             
  9.             # 记录左右的 max
  10.             lHight = max(height[:i])
  11.             rHight = max(height[i + 1:])
  12.            
  13.             # 计算面积 
  14.             res1 = min(lHight, rHight) - height[i]
  15.             if res1 > 0:
  16.                 res += res1
  17.         return res
'
运行

忽略左右两侧的单独柱子，对内部的柱子依次计算桶边 min(lHight、rHight) 和桶底 height[i] 的差距，大于0代表当前索引 i 可以接雨水的面积。根据 "你立马想到必不能过" 原理，如果我们想法清晰且简单快速实现，那么本题必出幺蛾子，继续想其他办法。

◆ ​​​​​​​循环利用

  1. class Solution(object):
  2.     def trap(self, height):
  3.         # 1.初始化左右 max 柱子
  4.         cur_height = len(height)
  5.         left_bound = [height[0]] + [0] * (cur_height - 1)
  6.         right_bound = [0] * (cur_height - 1) + [height[-1]]
  7.  
  8.         # 2.更新左右 max 柱子
  9.         for i in range(1, cur_height):
  10.             # 左柱子，所以是 i-1 和新来的 i 比大小
  11.             left_bound[i] = max(left_bound[i - 1], height[i])
  12.             # 右柱子，新来的 i 和之前的 i+1 比大小
  13.         for i in range(cur_height - 2, -1, -1):
  14.             right_bound[i] = max(right_bound[i + 1], height[i])
  15.  
  16.         # 3.木桶效应
  17.         re = 0
  18.         for i in range(1, cur_height - 1):
  19.             re += min(left_bound[i], right_bound[i]) - height[i]
  20.  
  21.         return re
'
运行

暴力法中我们对于每一个中间的柱子 mid 都分别向左向右找最大，这个过程其实是重复的，我们可以一次性把左边和右边柱子的最高高度记录下来，随后根据计算方法 min(l_h, r_h) - h 直接遍历计算即可，上面通过两个辅助 List left_bound 和 right_bound 分别记录，最后根据木桶效应计算，相比暴力法节省了很多重复寻找的时间。

◆ ​​​​​​​单调栈

  1.     def trap(self, height):
  2.         stack = [0]
  3.         result = 0
  4.         for i in range(1, len(height)):
  5.             while stack and height[i] > height[stack[-1]]:
  6.                 # 打印日志 print(stack)
  7.                 mid_height = stack.pop()
  8.                 if stack:
  9.                     # 雨水高度是 min(凹槽左侧高度, 凹槽右侧高度) - 凹槽底部高度
  10.                     h = min(height[stack[-1]], height[i]) - height[mid_height]
  11.                     # 雨水宽度是 凹槽右侧的下标 - 凹槽左侧的下标 - 1
  12.                     w = i - stack[-1] - 1
  13.                     # 累计总雨水体积
  14.                     result += h * w
  15.             stack.append(i)
  16.         return result
'
运行

单调栈的思路其实还是木桶原理，如果桶能够接到雨水，其一定是两边高中间低的情况，所以单调栈内栈底到栈顶是递减的，这里栈底相当于桶的左边，其余递减的元素相当于桶底，当遇到 height[i] > height[stack[-1]] 的情况时，说明对于栈顶所在元素索引 stack[-1] 而言，它桶的右边也找到了，所以就可以计算面积了。这里与前面暴力法竖的计算面积不同，单调栈采用横向面积计算，下面画图看一下，以下面 heigths = [5, 2, 1, 0, 4, 1, 1, 6] 为例，我们通过 stack 的情况分析计算过程:

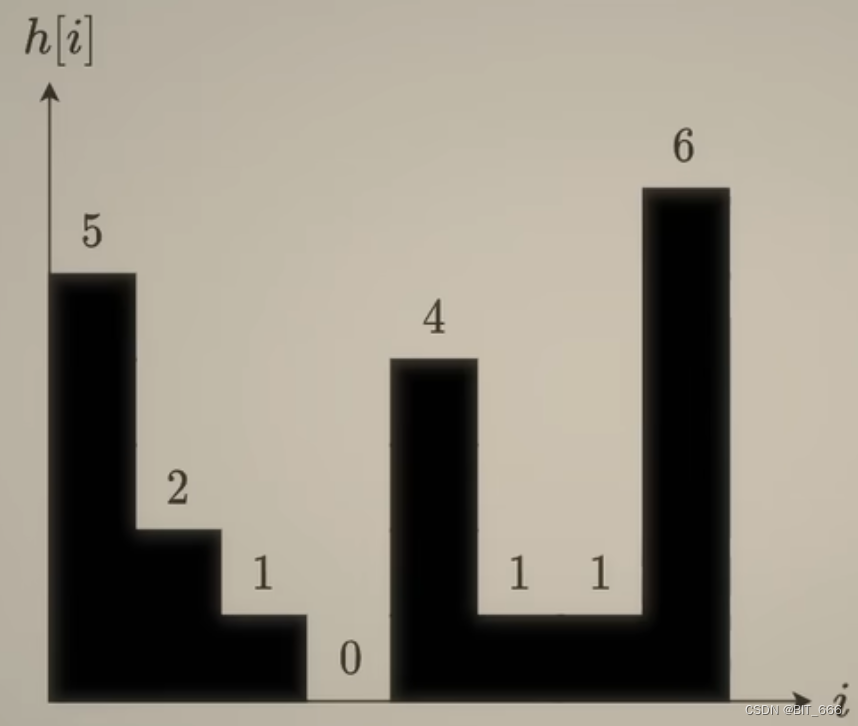
- [0, 1, 2, 3]

因为 5、2、1、0 是递减的，所以只执行 for 循环操作，while 判断的 height[i] > height[stack[-1]] 不执行，所以一次添加了 1、2、3 的索引。当遇到 heigth = 4 的时候，其满足 while 条件，此时对于 0 而言，可以计算其雨水面积: 

  1. mid_height = stack.pop() = 0 # 中间柱子
  2. h = min(height[stack[-1]], height[i]) - height[mid_height] # 水桶的低处
  3. w = i - stack[-1] - 1 # 雨水量

中间柱子高度为 0，h = min(1, 4) - mid_height = 1，面积为 1 x 1 = 1

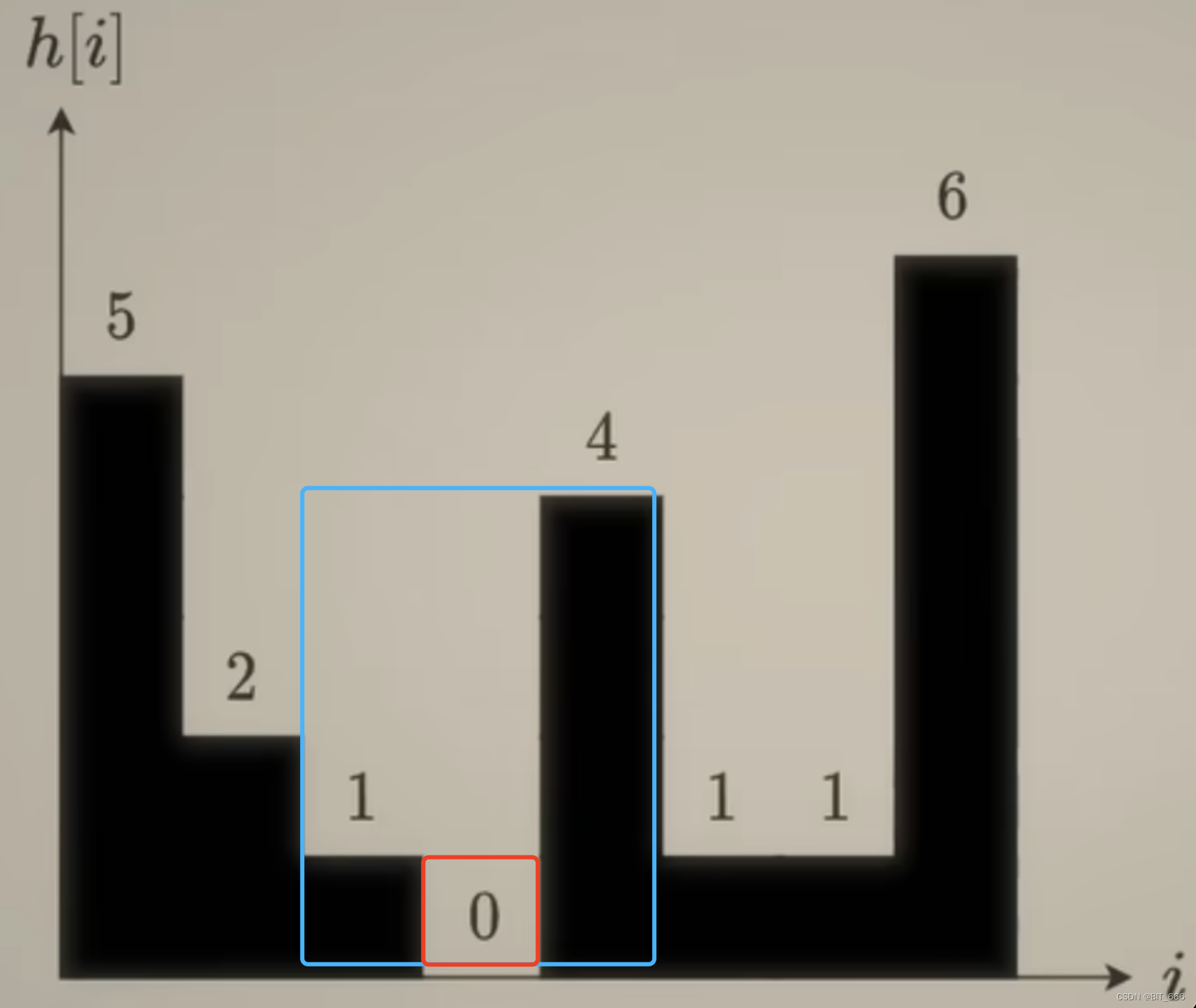
这里蓝框对应我们处理的三个元素，红框代表实际雨水面积。

-[0, 1, 2] -[0, 1]

这两个同上，因为 index=2 的 height=1 与 index=1 的 height=2 均小于 4，所以都会触发 while 逻辑计算面积，其面积如下所示，对于 index=2 而言，其对应面积为 2，index=1 而言面积为 6，这里计算完 mid = [index=1] 的棒子后，index=1 从 stack 中 pop，此时 stack 仅剩 [0]。

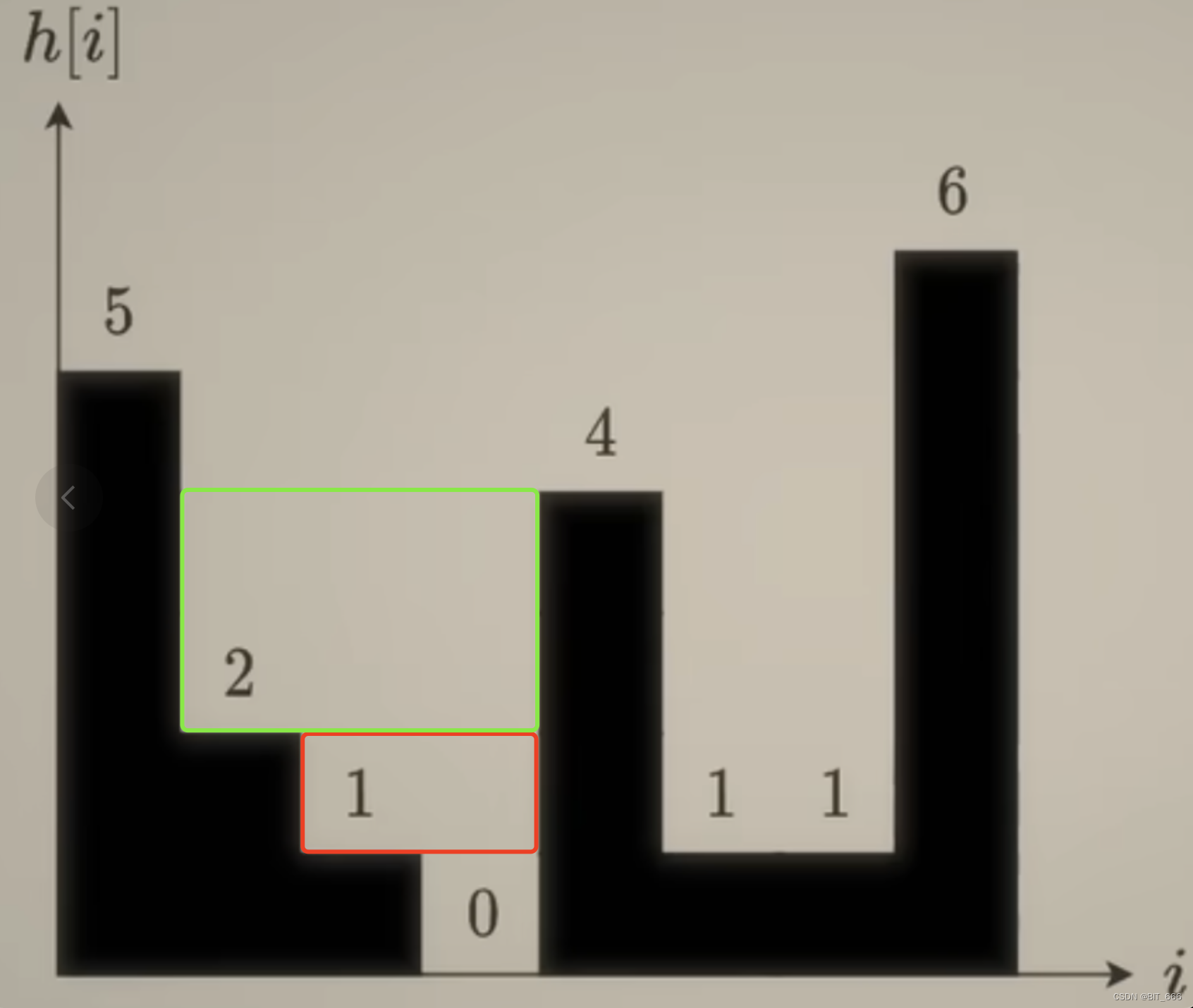
- [0, 4, 5, 6]

stack 剩下元素为 index = 0，height=5，由于后面的 4、1、1 对应的高度均小于5，所以他们的索引 4、5、6 均添加到栈中。此时元素 6 出现，其大于上一个 mid=1，所以开始计算雨水面积。其左柱子高度为1，右柱子高度为6，min(1,6) - mid_height = 0，所以索引 6 处对应的雨水面积为0，因为桶左边漏水。

- [0, 4, 5]

换到 index = 5 处的 1 时，其左柱子高度不再为 1，而是 4，所以 min(4, 6) - 1 = 3，此时宽度为 2，面积计算得6。

- [0, 4]

stack 将两个 1 弹出后，还剩 [0, 4]，此时 mid_height = 4，左柱子高度 5，右柱子高度 6，min(5, 6) - 4 = 1，但是宽度是 7 - 0 - 1 = 6，所以这里面积为 6。

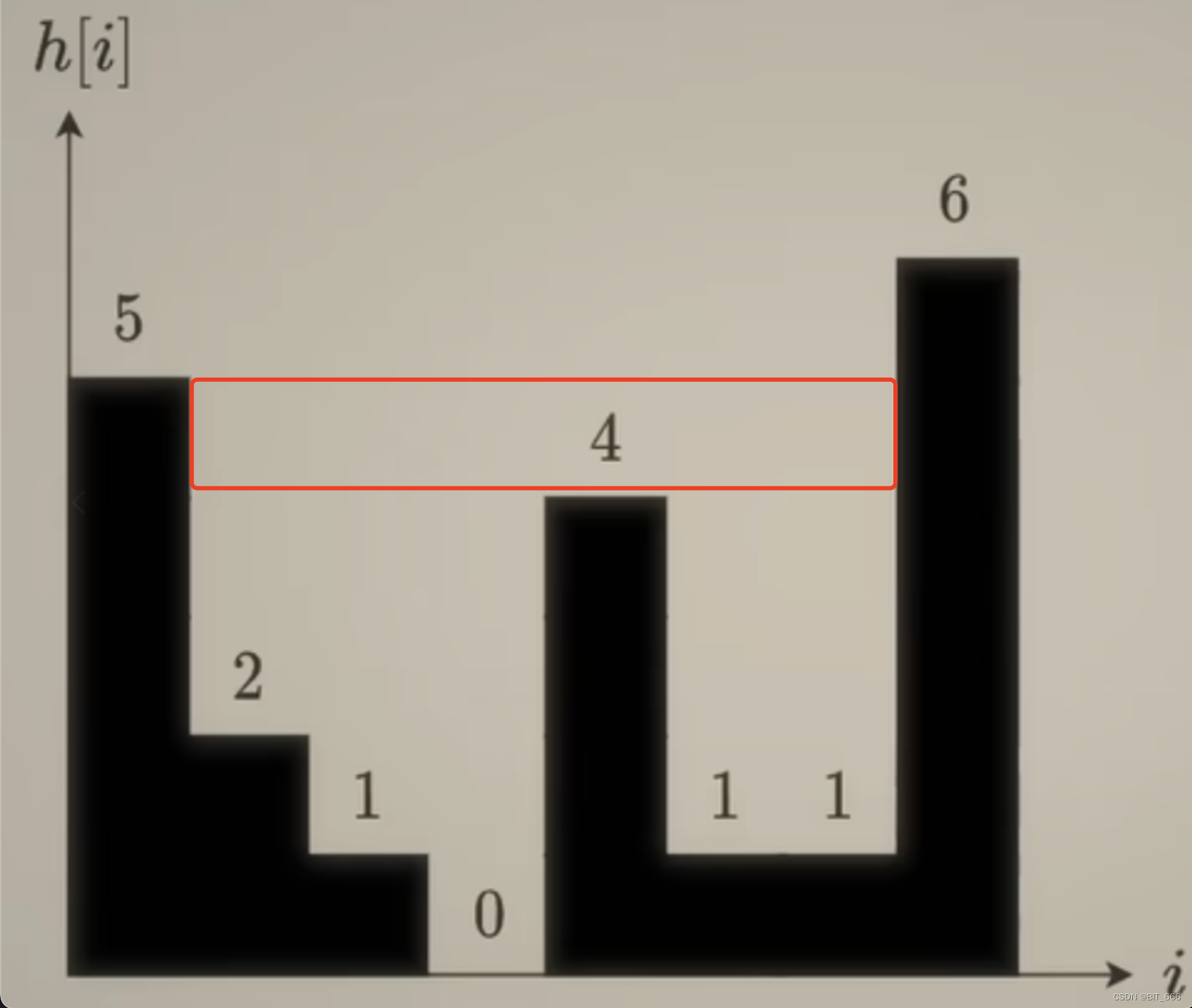
- [0]

mid = 4 的柱子索引弹出，height = 6 的索引进入 stack，这里满足 6>5 所以进入 while 逻辑，但是当 mid = index[0] 的中间柱子弹出后，不满足 if stack 条件了，所以遍历也就结束了，这是因为两个柱子不足以构成带底的水桶。综合上面的计算流程，我们其实是把水桶转了 90 度计算面积：

通过数形结合的方法，这道题的代码理解起来就不难了，难点在于单调栈的想法与实践，即什么时候需要使用单调栈。 单调栈就是保持栈内元素有序，当我们需要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置，就可以想到可以用单调栈了。而接雨水这道题目，我们需要寻找左右的最大元素，所以可以使用其来计算接雨水面积。

◆ ​​​​​​​二刷留念

  1. class Solution:
  2.     def trap(self, height):
  3.         
  4.         # 空桶
  5.         if len(height) < 2:
  6.             return 0
  7.  
  8.         res = 0
  9.  
  10.         # 维护左右边界
  11.         bound = [[0,0] for _ in range(len(height))]
  12.         bound[0][0] = height[0]
  13.         bound[-1][-1] = height[-1]
  14.  
  15.         left = height[0]
  16.         right = height[-1]
  17.  
  18.         # 左边最大
  19.         for i in range(1, len(height) - 1):
  20.             bound[i][0] = left
  21.             left = max(left, height[i])
  22.         
  23.         # 右边最大
  24.         right = height[-1]
  25.         for i in range(len(height) - 2, -1, -1):
  26.             left_bound = bound[i][0]
  27.             if height[i] < right and height[i] < left_bound:
  28.                 res += min(left_bound, right) - height[i]
  29.             right = max(right, height[i])
  30.         
  31.         return res
  32.  
'
运行

优化了遍历的次数，把左边边界和右边边界放在一个数组维护。这个题单调栈有些同学理解起来有困难或者想要最基础的解题方案，就可以考虑这个解法。

3.largest-Rectangle-Area [84]

最大矩形面积: https://leetcode.cn/problems/largest-rectangle-in-histogram

◆ ​​​​​​​题目分析

本题考察非负数组构成的列表表示的柱状图能够勾勒出的最大矩形面积，看到题目思考后，第一个思路比较快的出现，即遍历每一个柱子，向左向右寻找比其大的元素，使其能到达的最大宽度，这个方法很好理解，但是其时间复杂度为 o(n^2)，依照我们以往的惯例，这样大概率会在耗时上被卡掉。另外一种实现是利用单调栈，这个方法比较巧妙，一会看图理解一下。

◆ ​​​​​​​左右开弓

  1. class Solution(object):
  2.     def largestRectangleArea(self, heights):
  3.         """
  4.         :type heights: List[int]
  5.         :rtype: int
  6.         """
  7.         # 棒子数量
  8.         bar = len(heights)
  9.  
  10.         # 记录当前最大值
  11.         global_max = -1
  12.  
  13.         for i in range(bar):
  14.             # 记录当前 h 与 w
  15.             cur_height = heights[i]
  16.             cur_width = 1
  17.  
  18.             # 向左 声明：本文内容由网友自发贡献，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：【wpsshop博客】
    推荐阅读
    相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。