- 100. 这里整理了最全的爬虫框架(Java + Python)_java爬虫框架
- 2【愚公系列】软考高级-架构设计师 119-区块链
- 3分享一篇游戏测试的面试技巧_游戏测试常见面试题
- 4使用Fiddler进行App弱网测试、抓包断点,详细步骤_fiddler断点测试步骤
- 5LLM - 读取 Lora 模型进行文本生成_automodelforcausallm
- 6深入理解NPM依赖模型_npm对等依赖
- 7基于SpringBoot+Vue+uniapp的电商购物网站的详细设计和实现(源码+lw+部署文档+讲解等)_购物网站源代码
- 8多变量微分方程组带事件控制的ODE45函数写法
- 9大数据开发实战系列之Spark电商平台_spark 2.x企业级大数据项目实战(实时统计、离线分析和实时etl)
- 10ElementUI 年份范围选择器 el-year-picker_element选择年度范围
深度学习之:强化学习 Reinforcement Learning_深度强化学习
赞
踩
认识强化学习
- 一般我们知道 Machine learning 一般指的是传统方法(贝叶斯,决策树,逻辑回归等)模型来实现一些数据分析或者分类的任务,而深度学习则是基于深度神经网络发展出来的一系列更加强大的模型,这些模型根据功能可以分为 CNN,RNN, Transformer 等,他们往往基于大量的数据集来拟合数据的分布,从而获得非常强大的视觉或者语言能力。
- 无论是机器学习还是深度学习,都基于
Supervised learning或者Unsupervised learning又或者self-supervised learning来进行训练模型。 - 但 Reinforcement learning 则既不是监督学习也不是无监督学习,而是一种特殊的学习方式。而区别于 ML 和 DL 中常用的
label-based+ 梯度下降的训练方式。RL 倾向于一种全新的训练策略。 - 下面来看一下 RL 的核心思想:
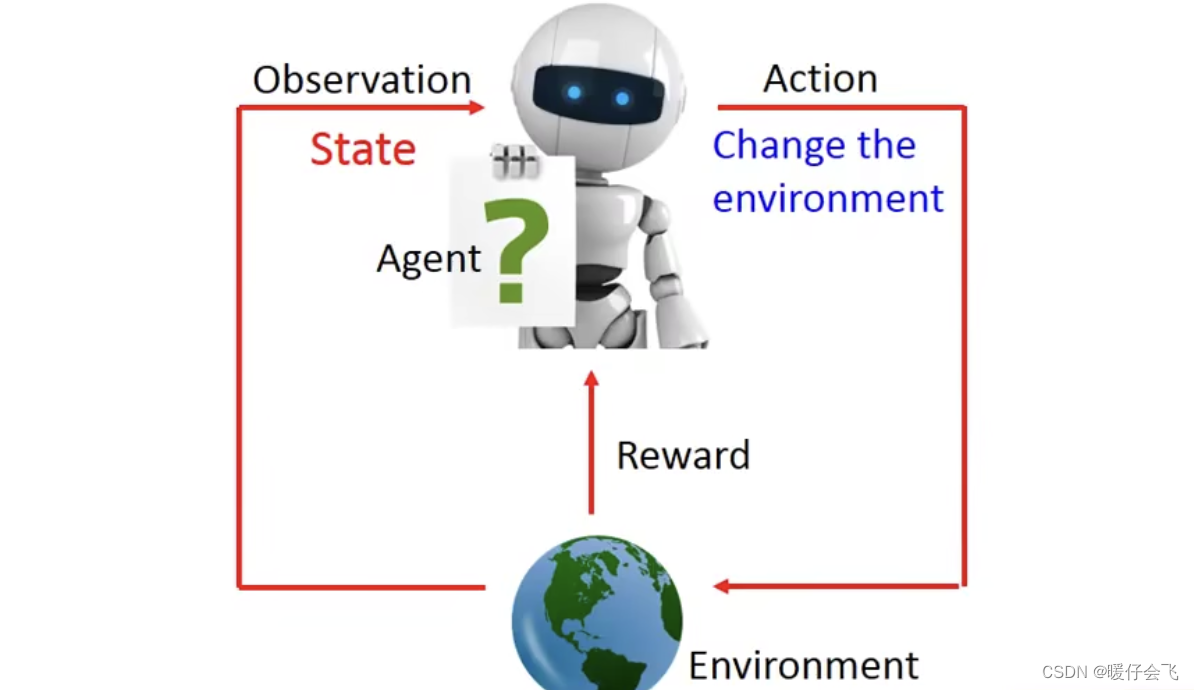
- RL 的核心构件包括:
- Agent:代理
- Environment:环境
- Agent 可以通过观察环境的状态(state)采取一个动作(action)
- 这个 action 会改变环境,从而使 agent 获得 reward 或者 penalty,从而 agent 可以不断地接收到来自环境的反馈来改进自己的行为。
- 而 RL 的目的就是学习一个 actor 函数,这个函数输入就是 environment 当前的 state,输出就是 agent 根据这个状态而采取的 action. 而这个学习的过程则是依靠 reward 进行的。理论上如果模型学的够好,actor 函数足够强大,那么 agent 根据环境可以做最正确的决策。
Sparse Reward
-
在下面的描述中,会使用以下缩写:
environment->eenvironment state->esaction->aReinforcement learning->RL
-
比如 alphaGo,在 0 0 0 时刻的 alphago 看到的
es是一个空棋盘,所以他选择a是下载某个地方一颗棋子
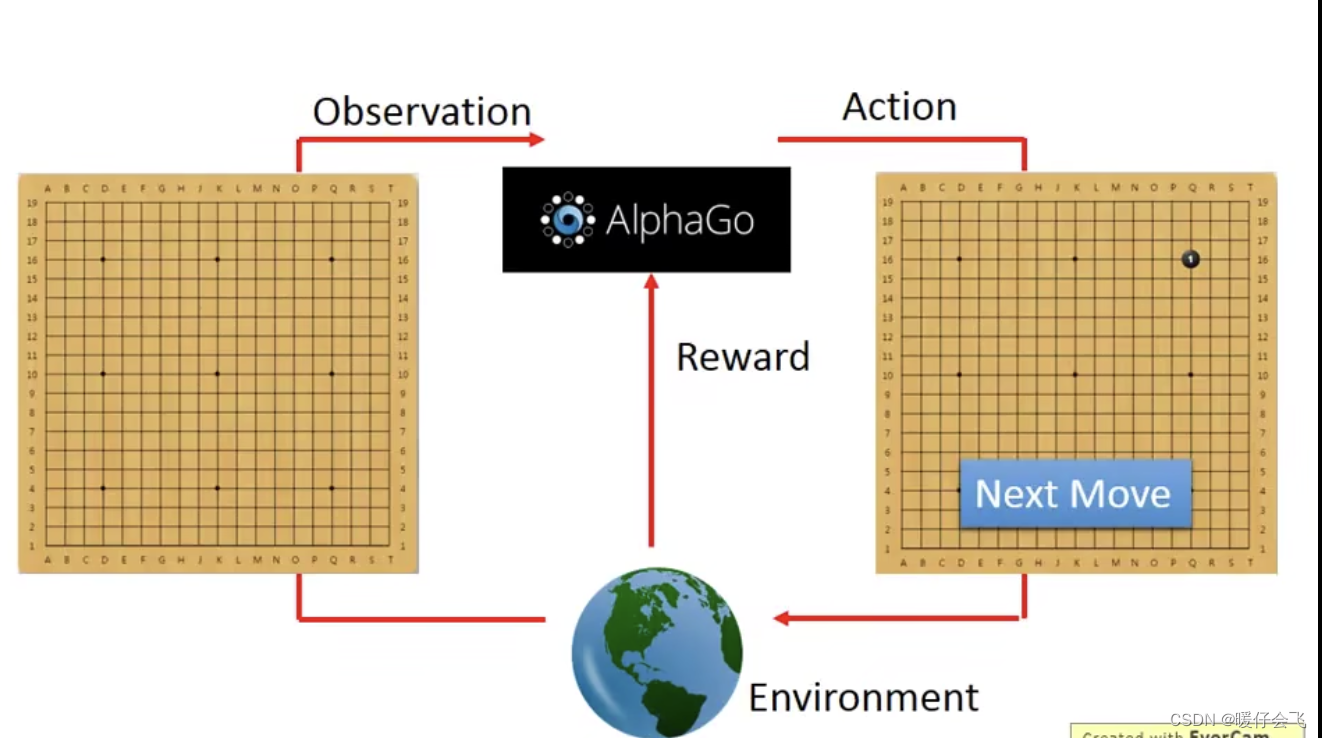
-
这个时候,对手就是
e,他会有所行动,也就是es发生改变:棋盘上多了一颗对方的白子
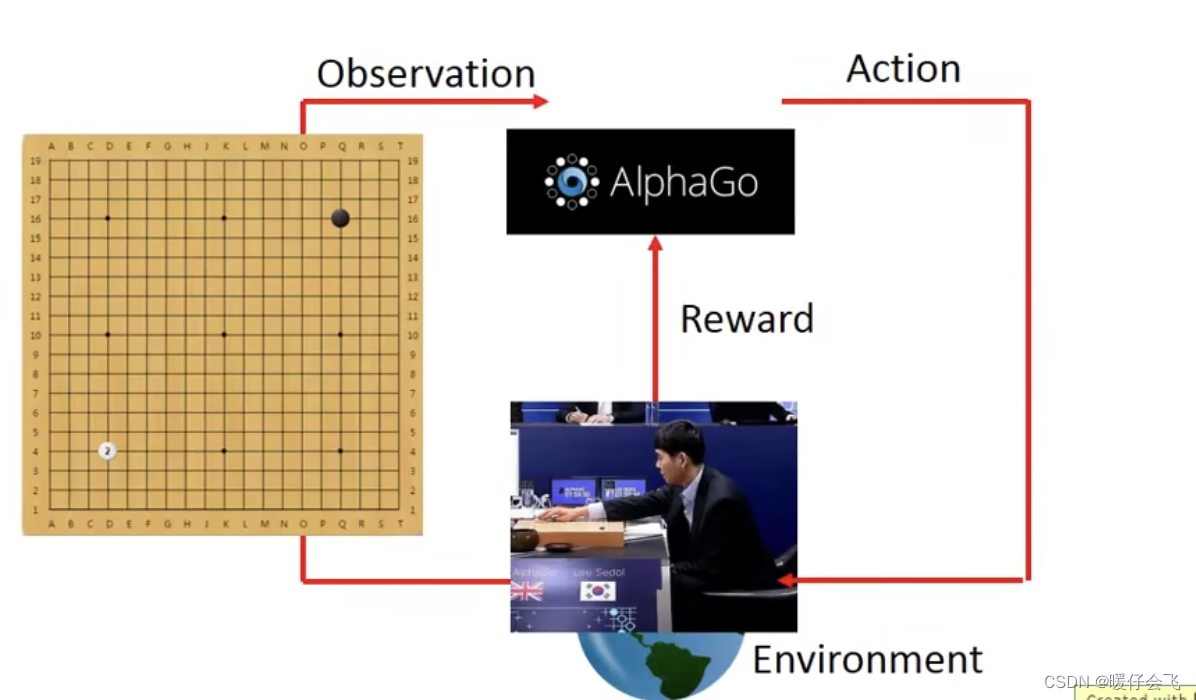
-
于是 alphago 根据当前的
es再采取新的a:下在另一个位置黑子
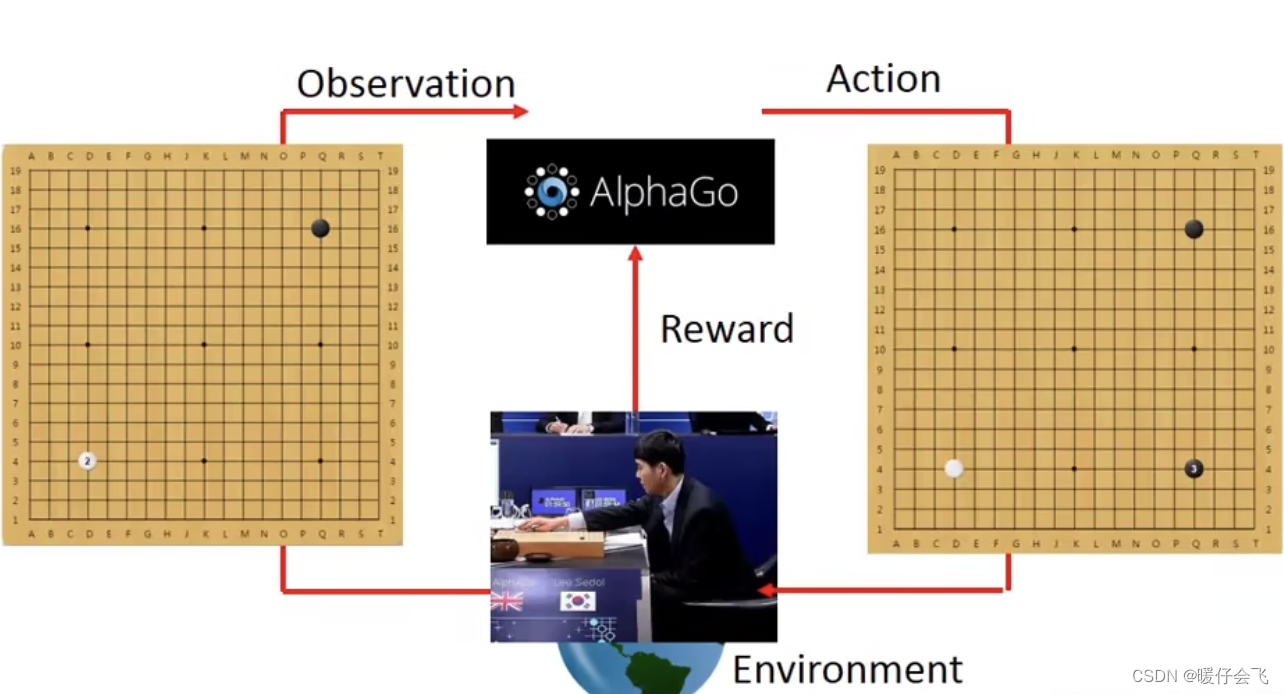
-
但是下棋这个任务非常特殊,因为如果我们把
对弈胜利的 reward=1,而对弈失败的 reward=-1 那么就会发现,只有在这个棋局的最后一个a之后才会产生 reward,其他步骤模型都没有得到任何的反馈,那么这个就非常不好,因为我们知道在我们熟知的一些监督任务中,每个 step 或者 epoch,模型都会根据当前的 loss 做梯度下降来更新参数。但是如果下棋只有最后一个步骤有 reward,那模型很难学到东西。这种困难的问题叫做sparse reward(稀疏奖励) 。这种问题在 RL 中是经常出现的。
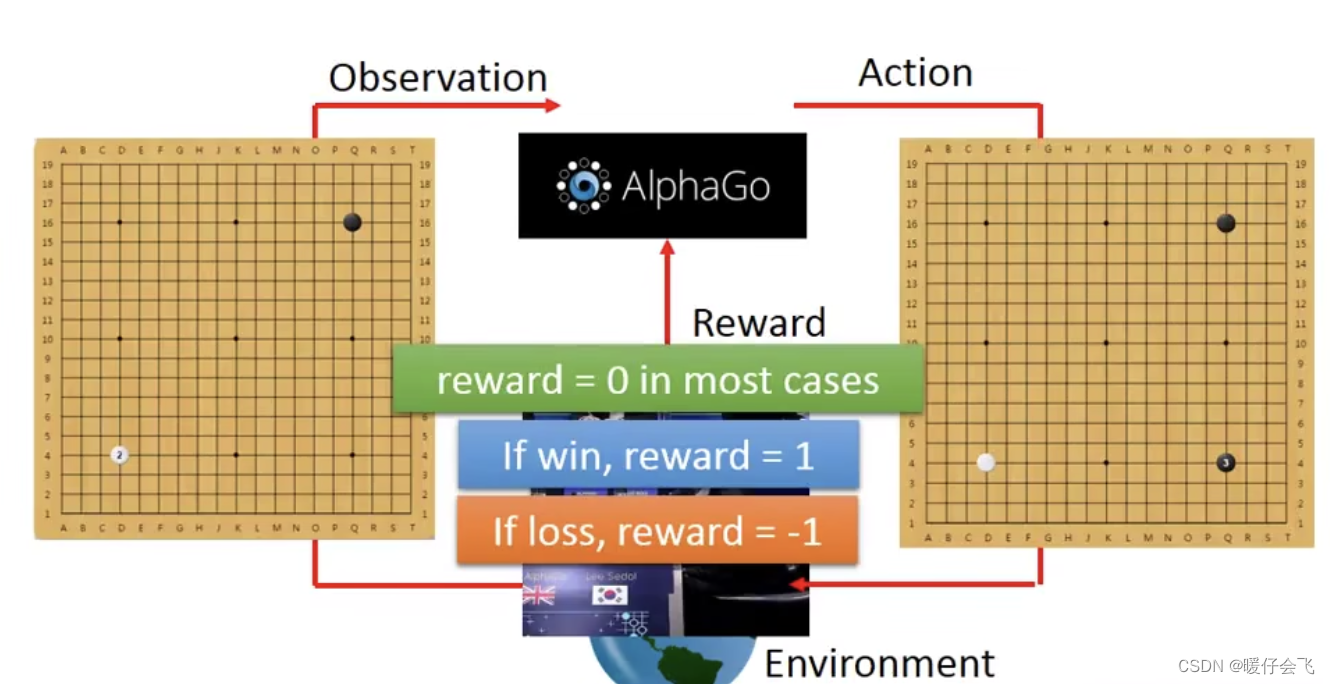
Supervised Learning v.s. RL
- 对于监督学习来解决这个下棋问题的话,往往会采用下面的方式:

- 即,给定一个局面,然后给出下一步的正确落子方式作为
label - 但是,这种方式的问题是:下棋这种决策性的游戏根据同样的环境是没有正确答案的。比如都是同一个棋局,高手可能会故意让对方吃掉自己一部分子来换得更大的胜利,所以死板地给定下一个落子位置的方式来训练模型是很死板的
- RL 则是通过让模型和不同的 对手(
e)进行下棋,然后根据大量的训练来获得真正的下棋能力,面对不同的对手都可以随机应变。 - 在下面的文章中,会介绍 RL 为什么可以随机应变(因为 RL 中存在大量的随机性操作,这也是为什么 RL 的训练不太容易收敛,而且非常耗时)
- alphago 的训练方式是
supervised learning + RL也就是先通过监督学习获得一个能力还行但很死板的初代版本,然后让两个 alphago 互相采用 RL 的方式进行对弈(3000万盘)
- 即,给定一个局面,然后给出下一步的正确落子方式作为
RL 玩游戏
-
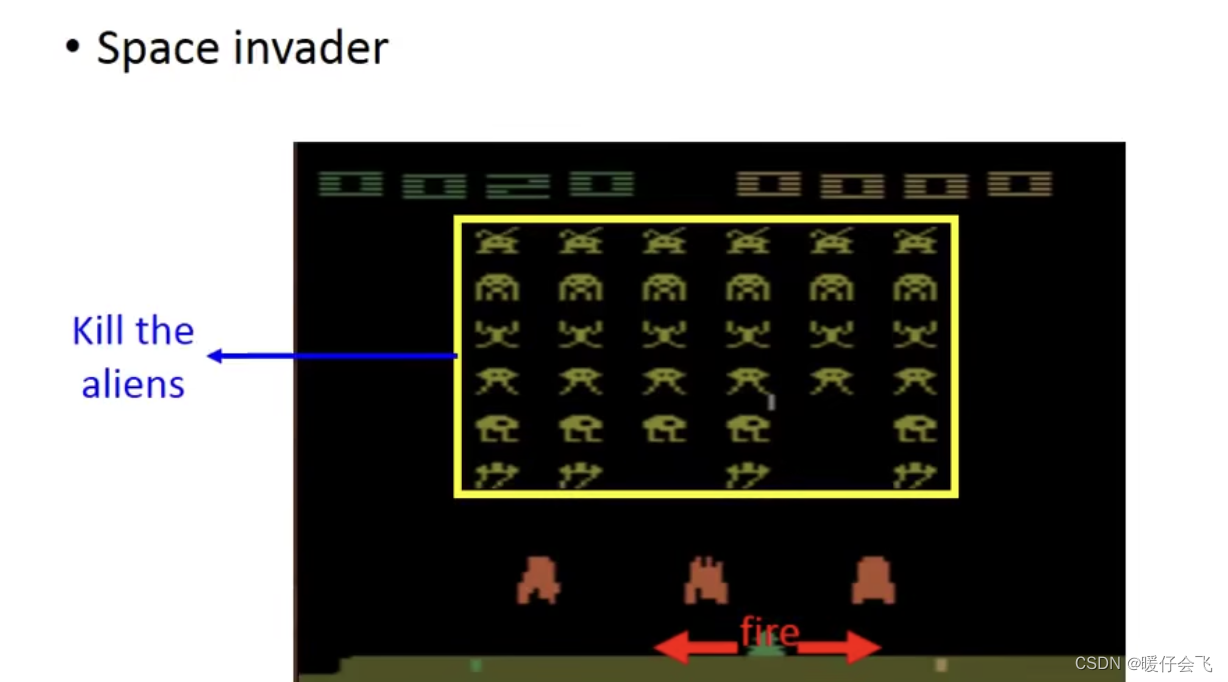
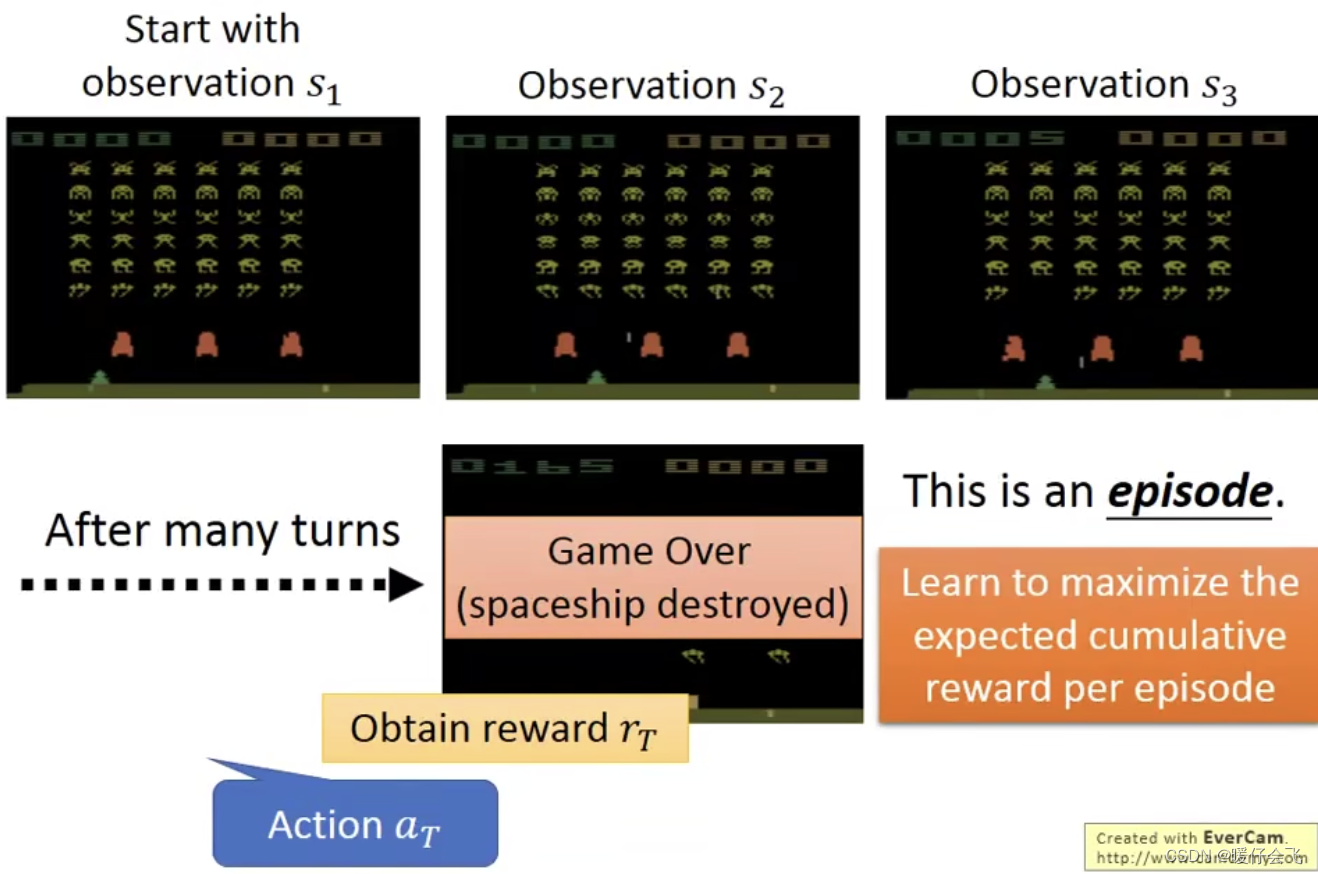
在这个游戏中, RL 负责操控最下面这个绿色的东西,他可以有三种操作
left, right, fire他的任务是负责杀死这些alien杀掉这些alien可以获得reward
-
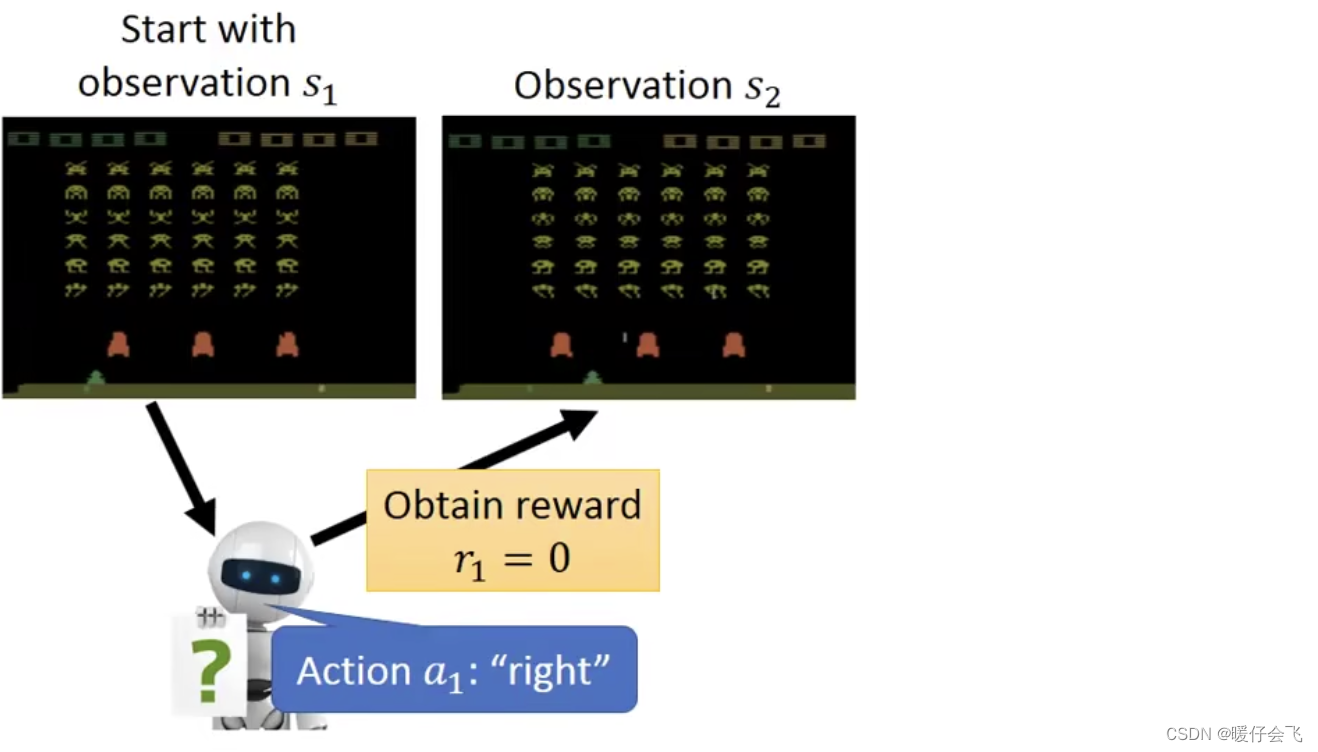
最开始的时候的
es是 s 1 s_1 s1 (es也叫 observation),根据这个画面,agent 采取的动作 a 1 a_1 a1 是向右移动,因此这个步骤的reward=0
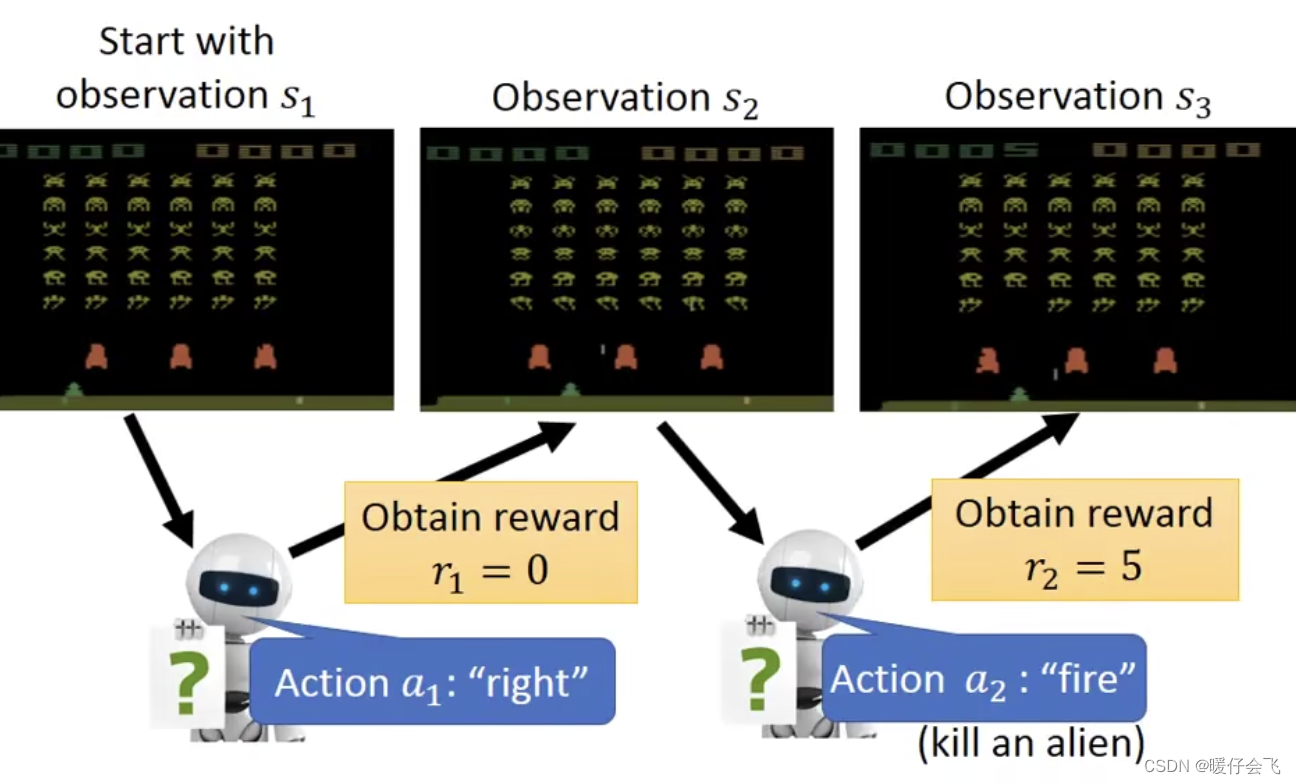
-
然后在 s 2 s_2 s2 的时候,agent 选择
fire并且成功射杀一个 alien,从而获得了reward=5的收益
-
经过了多个回合之后,最终 agent 采取了 a T a_T aT 获得了
reward为 r T r_T rT 然后游戏就结束了。 -
这一局游戏称为一个
episode,整个episode过程获得的reward的总和 r t o t a l r_{total} rtotal 是我们希望 maximize 的。 -
从这个过程中我们可以总结出 RL 的难点在于:
- reward delay:左右移动不会直接产生 reward,但是移到了正确的位置开火可以得到 reward,但是这个 reward 是滞后于左右移动这个行为的。因此如果模型只是根据 reward 来学习 action 的话,很有可能就是一直站在原地开火
- agent 的行为可能产生一些类的后续影响,也就是我们希望模型具有探索精神。比如如果模型觉得 fire 可以得到 reward 而一直 fire 但是却不进行任何的左右移动,那么这个模型就不具备 explore 的能力,结果也就不会太好
Policy-based & Value-based
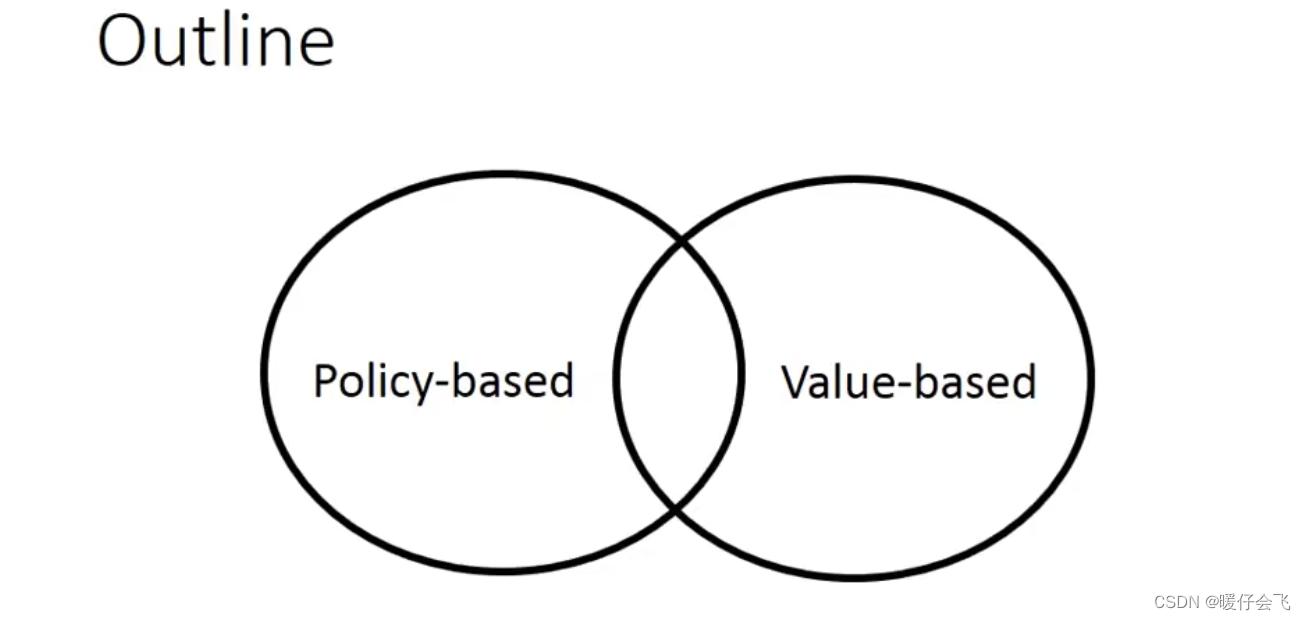
-
RL 的模型分成两个主要的分支:基于 policy 的方法和 基于 value 的方法;但是当前表现效果最好的 A3C 是将 value 和 policy 结合起来
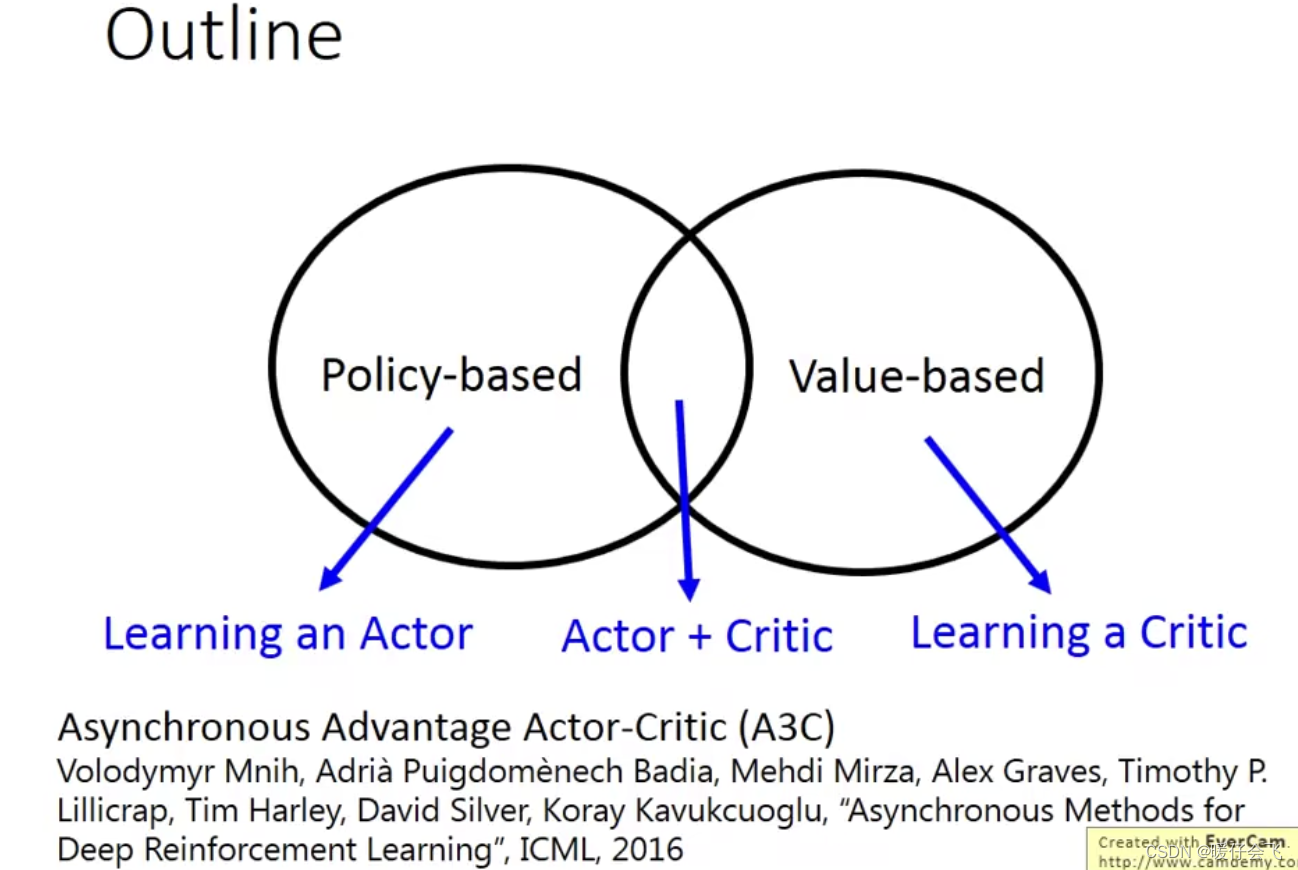
-
而 critic 的方式则是充当一个 批评者,通过不断纠正 agent 的行为来获得更好的结果
Policy-based
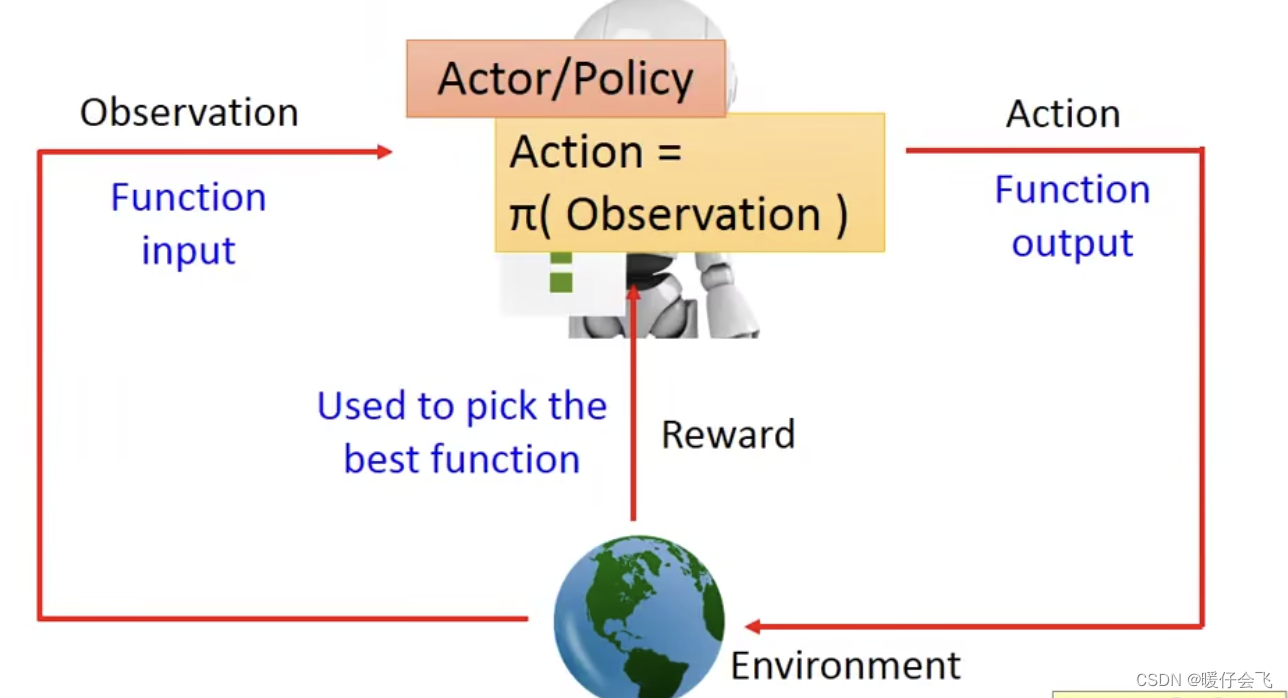
- 基于策略的方法本质上是训练一个
actor函数(也可以表示成 π \pi π),这个函数可以根据es(observation)输出一个最有效的a帮助 agent 获得最大的收益;actor函数在很多地方也叫做policy
训练模型的三步骤
- 任何深度学习 / 机器学习 / 强化学习 都可以分成三个步骤:
- 定义一个目标函数
- 判断这个目标函数是否足够好
- 将目标函数优化
定义目标函数
- 第一步:定义一个函数:这里的
actor就是这个函数
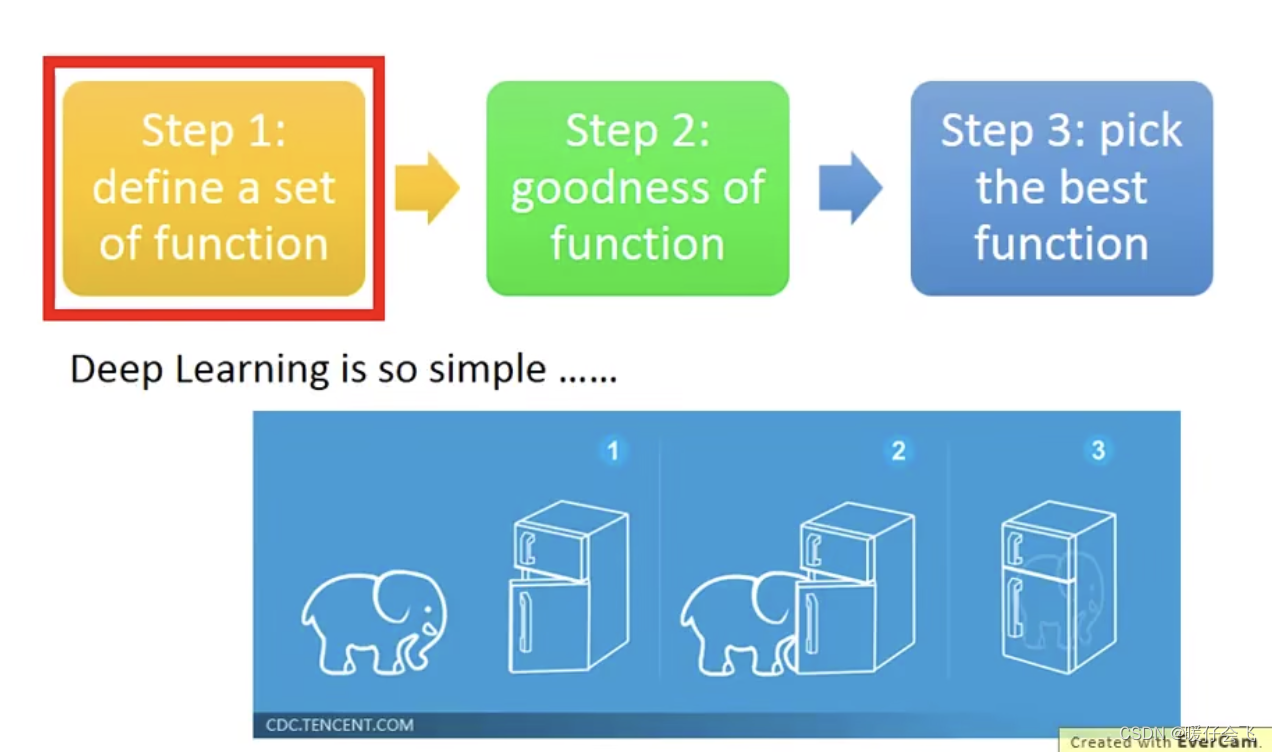
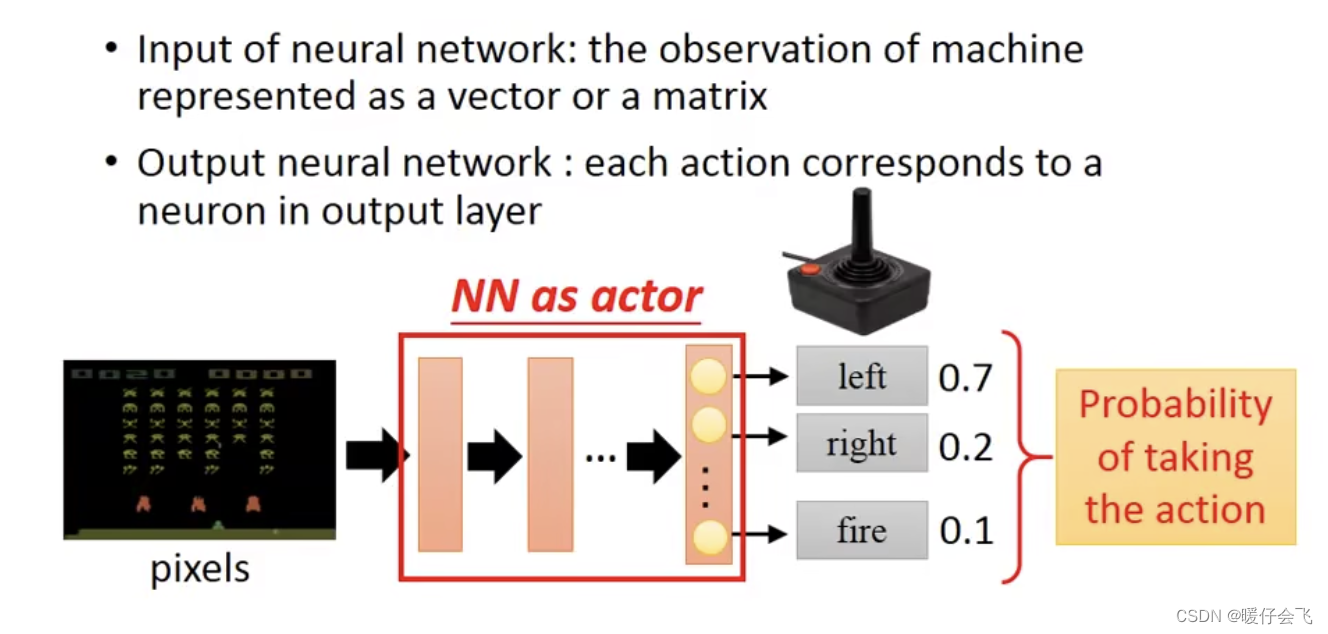
- 对于这个玩游戏的任务,那么输入是当前的环境状态(
es),在这里就是当前时刻的游戏影像,我们可以先通过 CNN 来提取这个图像的特征,然后把特征向量放到一个分类网络中得到最终是left, right, fire的三分类问题。在这里这个分类网络就可以看做是这个actor函数,因为他的输出就是针对当前影像的 action - 假设最后对于
left, right, fire的概率分布是0.7, 0.2, 0.1那么就代表有 70% 的几率是左移。但是不同于分类任务的是,RL 在这里并不会针对采取left这个 action,而是按照 0.7 的概率进行这个行为。(而普通的分类任务中,假设分类猫,狗的概率分布是0.7,0.3那么这个 sample 的predict_label=猫,但是 RL 并不如此)。
- 对于这个玩游戏的任务,那么输入是当前的环境状态(
衡量目标函数的好坏
- 第二步:判断这个目标函数的好坏
- 先看一下在普通的 supervised learning 中的判定一个目标函数好坏的方式:
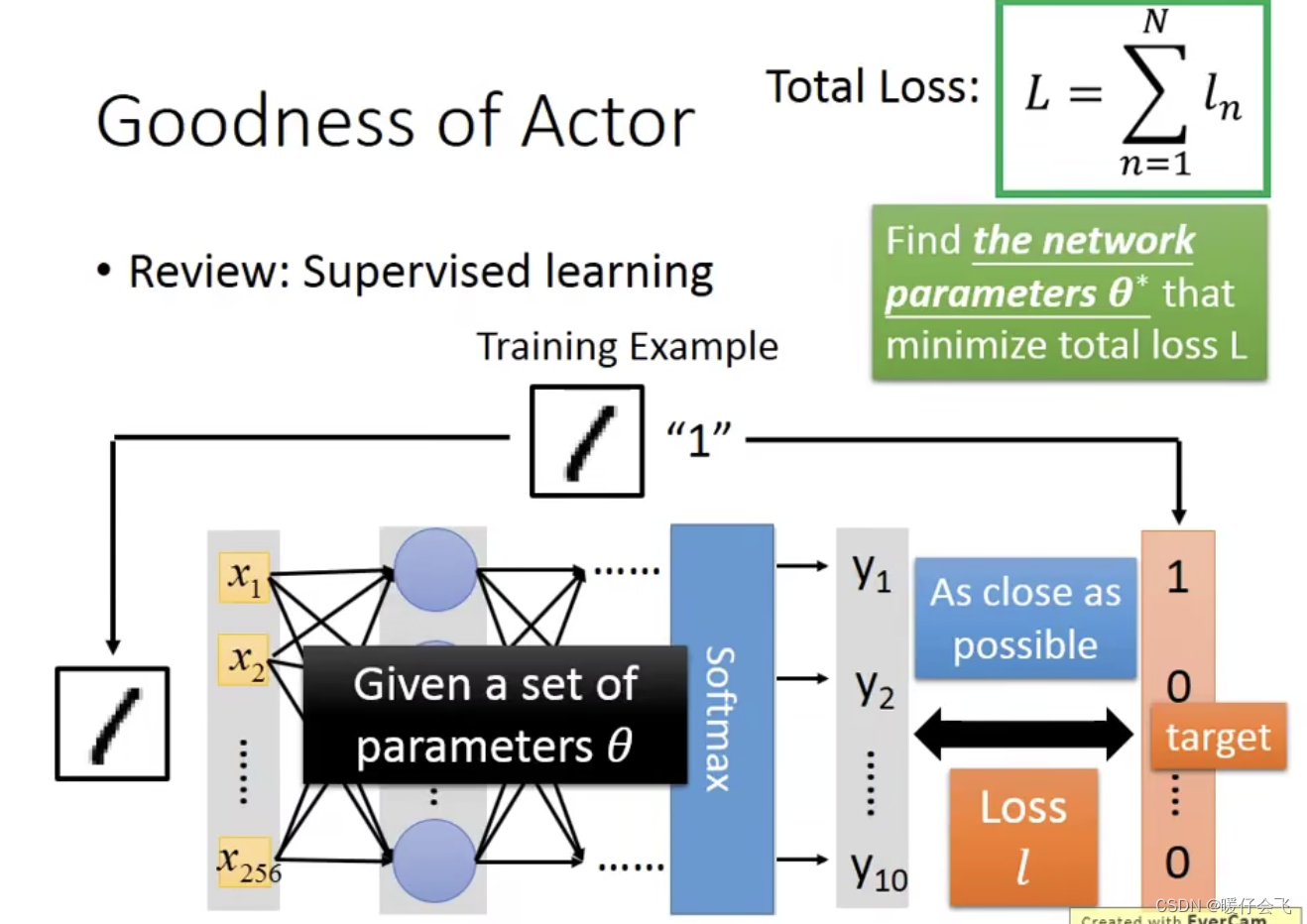
- 这个目标函数的参数我们用
θ
\theta
θ 表示,当一个 sample 经过目标函数得到的预测结果
predicted_label如果他和groundtruth的差距足够小,即loss(predicted_label, groundtruth)足够小,那么我们认为这个目标函数是好的 - 在 RL 中这个过程也是类似的
- 先看一下在普通的 supervised learning 中的判定一个目标函数好坏的方式:
RL 的目标函数的好坏(reward 总和的期望)

- 对于一个目标函数
π
θ
\pi_{\theta}
πθ 和某个时刻的
observations i s_i si,采取的action可以表示为 a i = π θ ( s i ) a_i = \pi_{\theta}(s_i) ai=πθ(si) - 而这个
a
i
a_i
ai 造成的收益
reward表示为 r i r_i ri - 如果在经过一整个
episode的游戏之后,整个过程的reward的总和可以表示为 R θ = ∑ t = 1 T r t R_{\theta}=\sum_{t=1}^Tr_t Rθ=t=1∑Trt - 如果 R θ R_{\theta} Rθ 非常大,那么我们就可以认为当前的 π θ \pi_{\theta} πθ 是足够好的。
- 但是我们在上面讨论过,当一个
s
s
s 输入
π
θ
\pi_{\theta}
πθ 的时候存在随机性,这种随机性表现在,即使是同一个
s
s
s 假设现在
π
θ
(
s
)
\pi_{\theta}(s)
πθ(s) 的分布表明
left, right, fire三种行为的概率分别为0.7,0.2,0.1那么第一次的结果可能是left这个action,但是第二次有可能是right因为虽然right的概率比left小,但是也是有概率发生的。这也就产生了一个问题,就是一次的 R θ R_{\theta} Rθ 并不能完全衡量 RL 目标函数的好坏,我们应该用 R θ ˉ \bar{R_{\theta}} Rθˉ 也就是 R θ R_{\theta} Rθ 的期望值来表示 RL 目标函数的好坏。 - 因此我们的优化目标是最大化
R
θ
ˉ
\bar{R_{\theta}}
Rθˉ ,这个优化过程我们依然可以采用梯度下降,那就是我们把
loss值,看做是 − R θ ˉ - \bar{R_{\theta}} −Rθˉ 然后最小化loss就可以得到我们想要的解。
如何求得 R θ ˉ \bar{R_{\theta}} Rθˉ
- 将一个
episode的过程看成一个trajectoryτ \tau τ,其中 τ = { s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , . . . s T , a T , r T } \tau=\{s_1, a_1, r_1, s_2, a_2, r_2,...s_T, a_T, r_T\} τ={s1,a1,r1,s2,a2,r2,...sT,aT,rT}
R ( τ ) = ∑ n = 1 N ( r n ) R(\tau)=\sum_{n=1}^N(r_n) R(τ)=n=1∑N(rn)
- 如果使用一个
actor函数 π θ \pi_{\theta} πθ,那么理论上会有很多个不同的 τ \tau τ,我们假设当前 τ \tau τ 出现的概率是 P ( τ ∣ θ ) P(\tau|\theta) P(τ∣θ) 因为这个 τ \tau τ 的出现概率是跟这个目标函数的参数 θ \theta θ 相关 - 因此我们可以表示当前
episode的reward的期望为:
R θ ˉ = R ( τ ) P ( τ ∣ θ ) \bar{R_{\theta}}=R(\tau)P(\tau|\theta) Rθˉ=R(τ)P(τ∣θ)
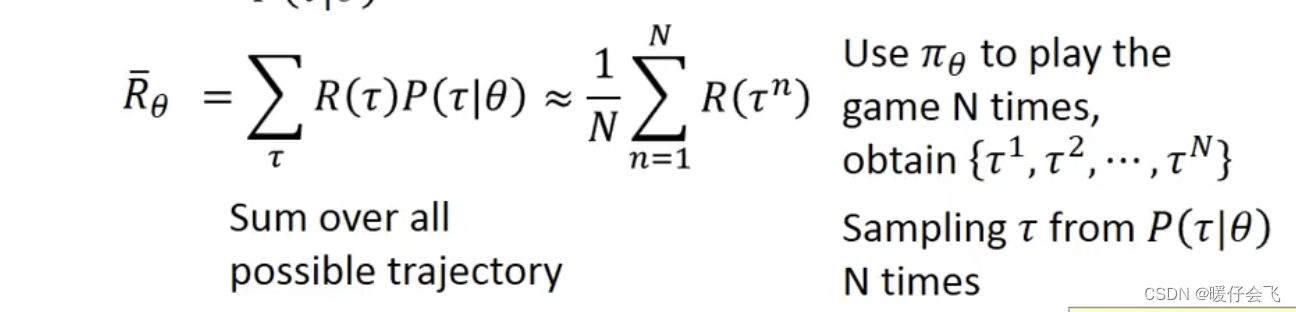
- 又因为
τ
\tau
τ 的情况是非常多的,我们不可能进行穷举,所以我们只能对
P
(
τ
∣
θ
)
P(\tau|\theta)
P(τ∣θ) 进行近似。我们让这个
agent在actor函数参数不变的情况下(使用同一个 π θ \pi_{\theta} πθ)进行 N N N 次游戏, N N N 次游戏的结果可以表示为 { τ 1 , τ 2 , . . . τ N } \{\tau^1, \tau^2, ...\tau^N\} {τ1,τ2,...τN} 这个过程相当于从概率分布为 P ( τ ∣ θ ) P(\tau|\theta) P(τ∣θ) 的分布中采样 N N N 次。 - 所以上图中左边的求和公式可以近似于右边的求和公式,所以我们将使用如下公式来计算出一个
episode的reward期望值,从而衡量当前的目标函数的好坏
1 N ∑ n = 1 N R ( τ n ) \frac{1}{N}\sum_{n=1}^NR(\tau^n) N1n=1∑NR(τn)
优化目标函数

-
因为我们要最大化 R θ ˉ \bar{R_{\theta}} Rθˉ 因此,我们采用
gradient asent的方法,当然也可以取负号,然后用gradient descent进行优化,都是一样的。

- 对于上面的公式,我们可以知道因为 R ( τ ) R(\tau) R(τ) 与 目标函数的参数 θ \theta θ 根本没关系,所以只需要对 P ( τ ∣ θ ) P(\tau|\theta) P(τ∣θ) 进行微分计算即可
- 根据 l o g ( f ( x ) ) log(f(x)) log(f(x)) 的微分法则,我们可以最终将公式化简成红框所在的那一行
- 然后根据我们上面近似的结果进行替换,可以得到最后一行的结果
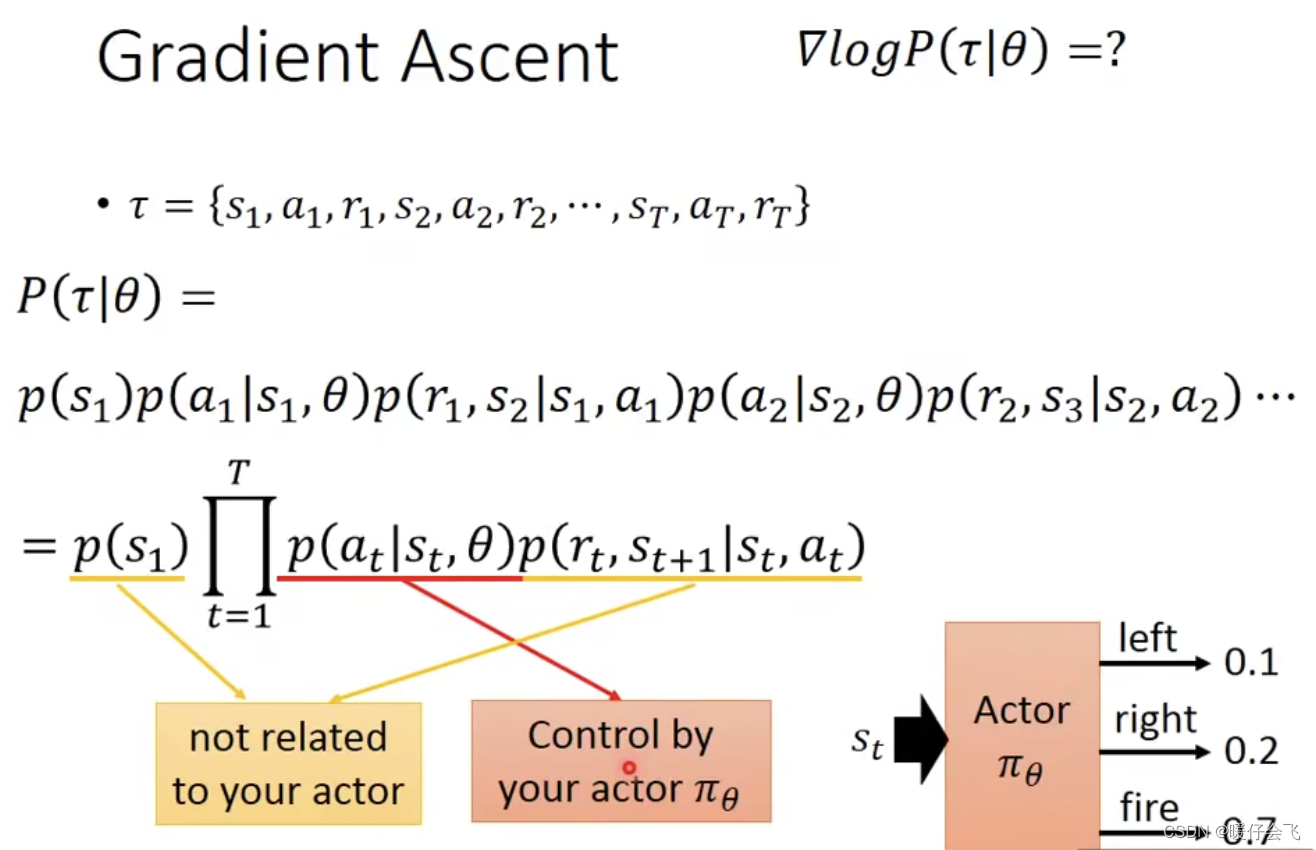
- 又因为 τ \tau τ 是一个序列,那么这个序列出现的概率可以按照上图中进行化简
- 因为 s s s 统统与 θ \theta θ 无关,所以开始是 p ( s 1 ) p(s_1) p(s1) 而 a 1 a_1 a1 的发生与 s 1 , θ s_1,\theta s1,θ 都有关,因此第二项是 p ( a 1 ∣ s 1 , θ ) p(a_1|s_1,\theta) p(a1∣s1,θ) 同样的,后面的概率都是这么写出来的
- 经过最终的化简之后可以看到,只有
p
(
a
t
∣
s
t
,
θ
)
p(a_t|s_t,\theta)
p(at∣st,θ) 与
θ
\theta
θ 有关

- 再化简,
l
o
g
log
log 运算无非是把连乘变成连加运算,然后将与
θ
\theta
θ 无关的项目从式子中剔除,就得到了最后的公式
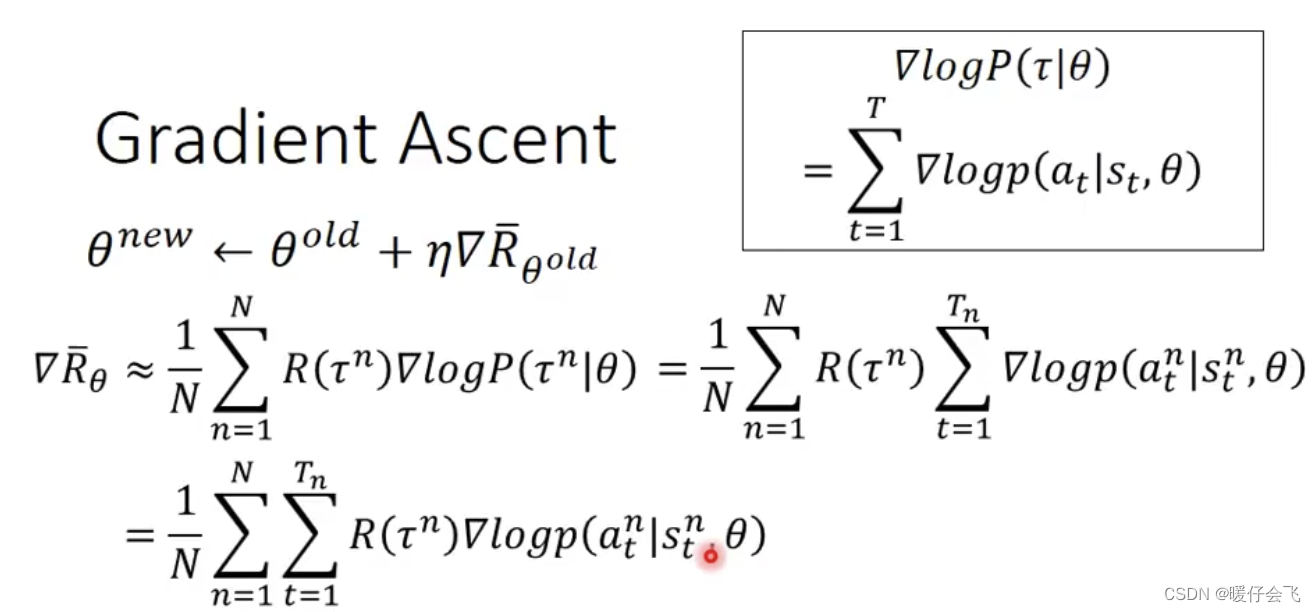

-
从这个式子看, ∇ R θ ˉ \nabla \bar{R_{\theta}} ∇Rθˉ 代表的是整个 目标函数的优化方向,而根据最终的式子来看,这个公式非常直觉,因为如果把公式里面只保留最重要的部分,也就是:
∇ R θ ˉ = R ( τ n ) ∇ l o g p ( a t n ∣ s t n , θ ) \nabla \bar{R_{\theta}}=R(\tau^n)\nabla logp(a_t^n|s_t^n,\theta) ∇Rθˉ=R(τn)∇logp(atn∣stn,θ) -
当使用 π θ \pi_{\theta} πθ 作为
actor函数时,当面对 s t n s_t^n stn 这个environment state,此时如果 R ( τ ) > 0 R(\tau)>0 R(τ)>0 那我们希望调整参数 θ \theta θ 来让 p ( a t n ∣ s t n ) p(a_t^n|s^n_t) p(atn∣stn) 的概率越大越好,当 R ( τ ) < 0 R(\tau)<0 R(τ)<0 则希望面对 s t n s^n_t stn 时,减小 a t n a_t^n atn 的概率。 -
可能理解起来稍微有些绕,好好想想,其实这个结论非常符合常识和直觉
-
但是这个式子仍然存在一个小问题,就是 R ( τ n ) R(\tau^n) R(τn) 有可能全都是正数,这可能造成一部分问题就是所有的行为 a i a_i ai 都是被鼓励发生的(更详细的解释可以参考李宏毅老师的视频,在一小时01分钟左右)
-
为了解决这个问题,人们让 R ( τ n ) R(\tau^n) R(τn) 减一个 baseline 的值,从而构造出 R ( τ n ) R(\tau^n) R(τn) 有正有负的情况

-
至于这个 b b b 是怎么算出来的,我们后面再说。
Policy-based RL 的一点补充
- 参考视频:李宏毅 强化学习 (Reinforcement Learning, RL) 2021
- 我们根据上面的知识,我们试图最优化一个
episode的总的reward值。这种做法其实可以看做是 version 0 ,但这种做法存在很大的问题,下面的内容就是不同的 version 存在的问题以及如何通过下一个 version 进行修正。
Version 0
- 为了简化,我们还是用以下缩略符号来表示对应的含义:
environment->eenvironment state->esaction->aReinforcement learning->RL
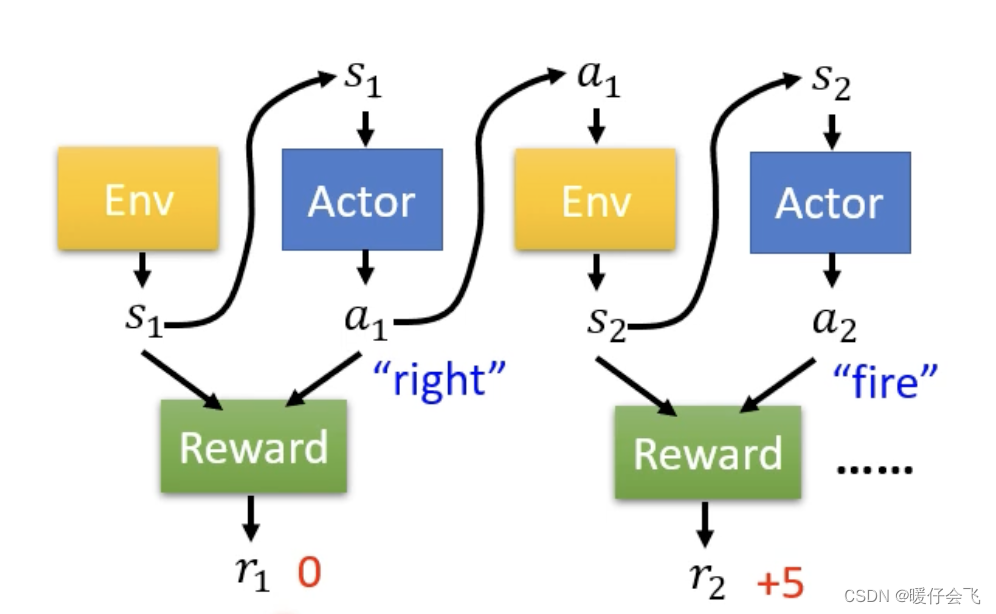
- 从第一个环境状态
s
1
s_1
s1 开始,将
s
1
s_1
s1 输入
actor函数得到 a 1 a_1 a1 同时产生 r 1 r_1 r1(第一个action对应的reward),然后以此递推下去,直到这个episode结束,那么所有的reward的总和就是
R = ∑ n r i R=\sum^nr_i R=∑nri - 这种做法的问题是:只有那些为
reward增大贡献的 a a a 会被越来越重视。就像上图中right这个行为本身不产生reward,fire产生reward所以如果按照version 0这个 agent 就会一直选择开火,而不移动,但我们都知道移动对于fire来说是很重要的。所以这种优化目标会让模型变得短视
Version 1

- 将从
a
1
a_1
a1 向后的所有动作产生的
reward相加得到 a 1 a_1 a1 的累加rewardG 1 G_1 G1 来代替version 0当中的 r 1 r_1 r1,同样的,可以得到 G 2 , G 3 , . . . , G N G_2, G_3,...,G_N G2,G3,...,GN - 这样做的好处是,后面的成功也会归因到前面的步骤,从而避免优化目标函数的时候忽略了这些自身
reward比较低的action - 所以这时候的优化目标就变成了 ∑ N G i \sum^NG_i ∑NGi
- 但是
version 1仍然也存在问题:当整个episode步骤过于长的时候,将第 N N N 步的reward归功于 r 1 r_1 r1 未免太牵强了。因此version 2采取了discount factor
Version 2
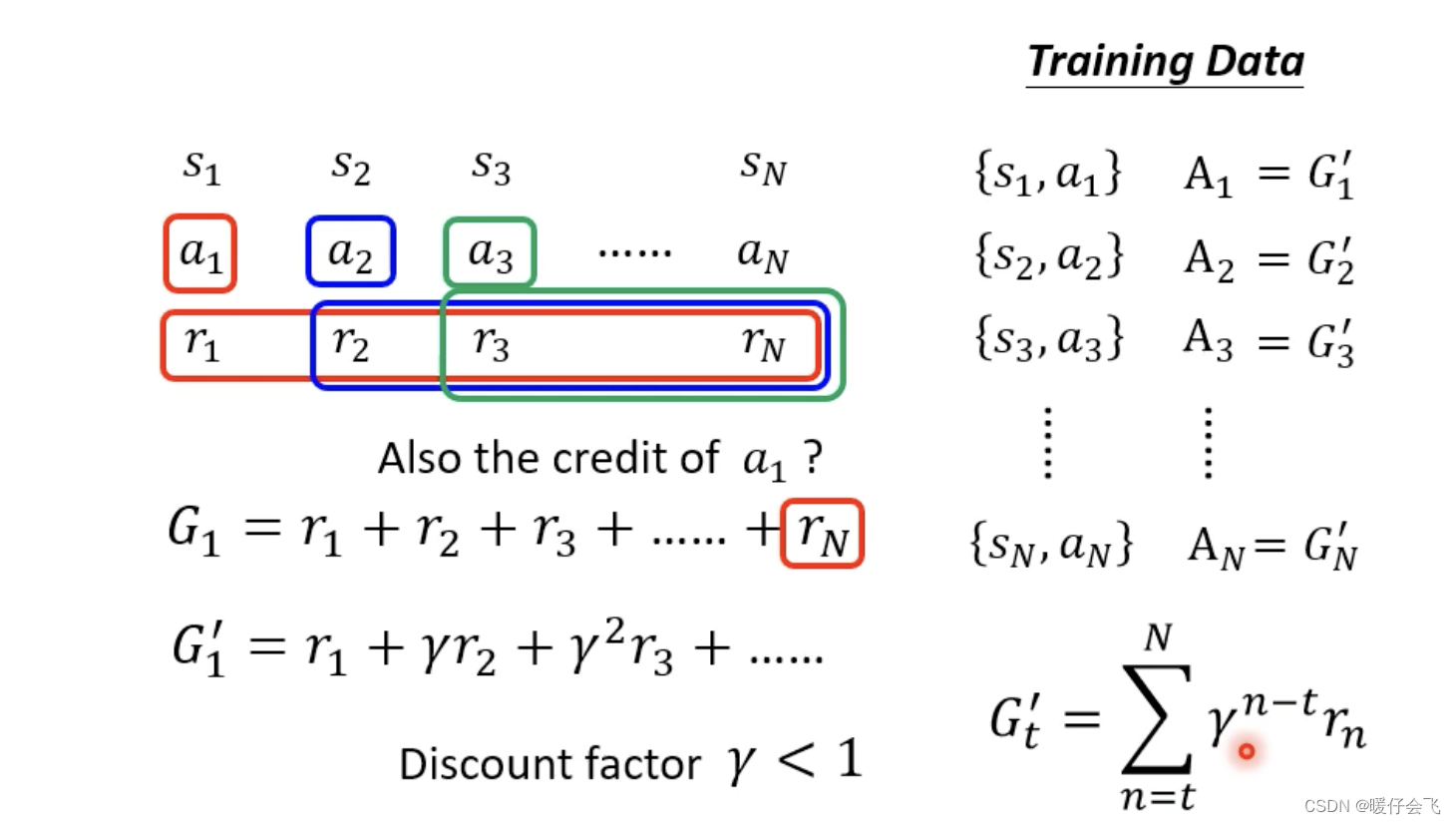
- 保留
version 1的主要思想,但是在计算 G G G 的时候,对于前面的action的reward都乘一个衰减系数 γ \gamma γ,就是说:我承认前面步骤的影响,但是离我越远的action对我的影响应该越小 - 按照这种思路,可以生成
G
1
′
,
G
2
′
,
.
.
.
,
G
N
′
G_1^{'},G_2^{'},...,G_N^{'}
G1′,G2′,...,GN′,优化目标也就变成了:
∑ N G N ′ \sum^NG_N^{'} ∑NGN′
插入一个小问题:
虽然现在的目标函数被定义的越来越完善,但是对于围棋这种只有最后才有reward而中间没有reward的操作,看起来还是束手无策啊。
- 但其实如果按照上面的目标函数去解决下围棋的这种情景,那么假设最后下棋赢了,那么就会认为所有的步骤都是
postive的,有效的,而如果输了,那么所有的步骤都是negative的- 虽然这看起来好像很离谱,但是初代的 alphago 就是这么训练的。
- 因为并不是一盘棋,是下几千万局,这个过程中有赢有输,每个
action的reward会调整很多次,所以虽然很难 train 但是还是可以 train 出来
Version 3
version 3是对version 2进一步优化,优化的方式是将每一项的 G ′ G^{'} G′ 变成 G ′ − b G^{'}-b G′−b 这个我们在上面提过。因为有些场景下,如果所有的 G ′ G^{'} G′ 都是正值,那么就不太好,所以我们倾向于让他们减去一个共同的数据 b b b 来保证过程中的 G ′ G^{'} G′ 有正有负。这种方法可以看成是一种标准化- 如何设置 b b b 呢?
如何设置 b b b
Policy Gradient

- 首先初始化参数
- 然后按照
epoch进行循环 ( E i , . . . , E T E_i,...,E_T Ei,...,ET),每个epoch中执行:- 使用上一个
epoch的actor函数(参数表示为 θ i − 1 \theta^{i-1} θi−1) - 将
s
1
,
.
.
.
,
s
N
s_1, ... ,s_N
s1,...,sN 的数据输入
actor得到 a 1 , . . . , a n a_1, ..., a_n a1,...,an - 接着计算出每个
action对应的rewardA 1 , . . . , A N A_1,..., A_N A1,...,AN - 根据这些
reward得到损失函数(或者优化目标) - 采用梯度下降或梯度上升来优化目标函数的参数
- 使用上一个
- 但是非常神奇的是,我们之前接触的一些项目,都是把数据在
epoch之外先整理好,但是RL训练过程中数据的收集是在epoch内部完成的,那为什么收集一次数据只能用于一个epoch迭代,而不能一直用呢?
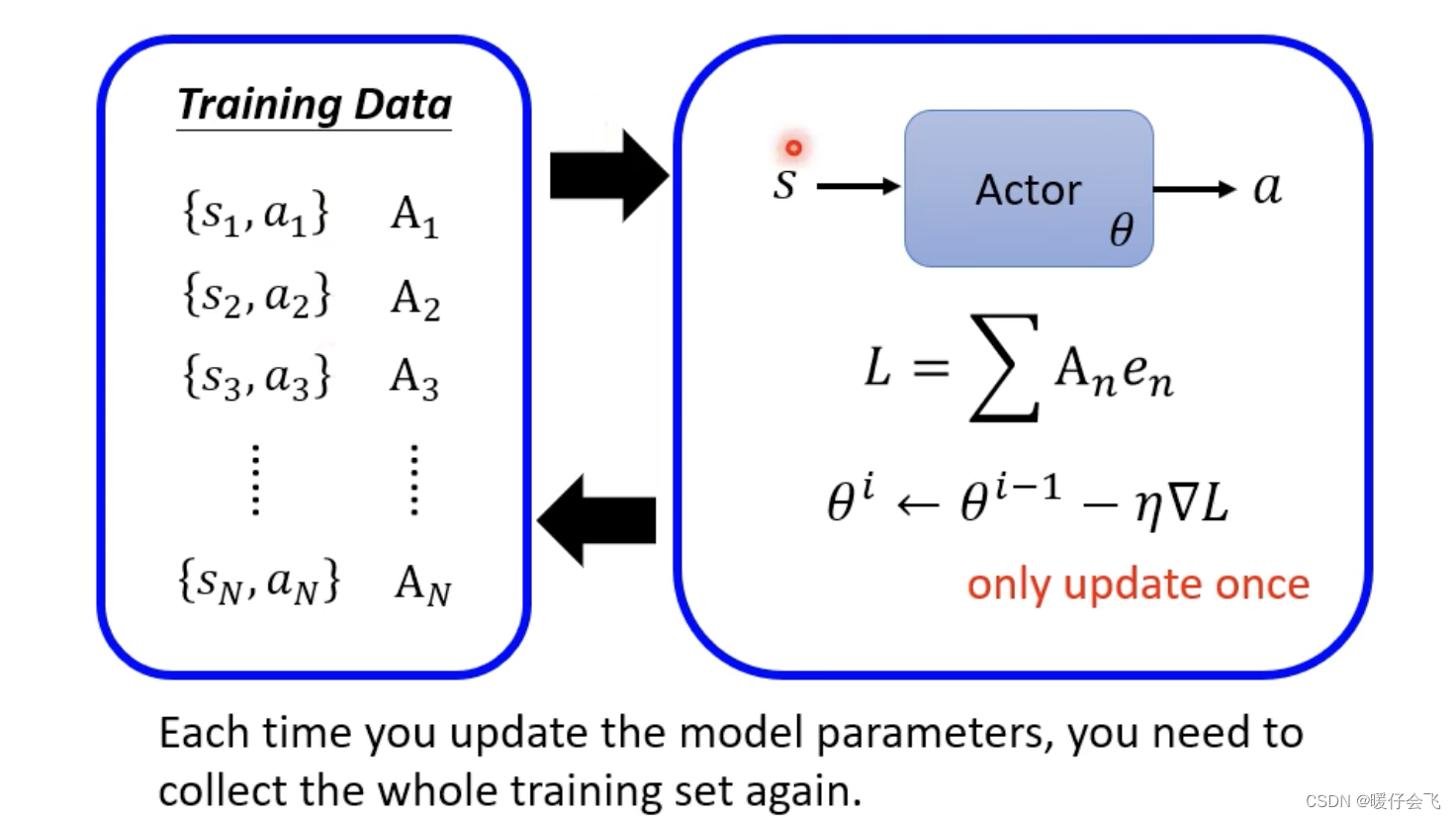
- 开始时第一个
epoch的actor参数是 θ 1 \theta_1 θ1 然后根据这个actor产生的 τ = { s 1 , a 1 , G 1 ′ , s 2 , a 2 , G 2 ′ , . . . , s N , a N , G N ′ } \tau=\{s_1, a_1, G^{'}_1, s_2, a_2, G^{'}_2, ..., s_N, a_N, G^{'}_N\} τ={s1,a1,G1′,s2,a2,G2′,...,sN,aN,GN′} 将actor的参数更新成了 θ 2 \theta_2 θ2 那么这个时候根据 s 1 s_1 s1actor会产生 a 1 ^ \hat{a_1} a1^和 G 1 ′ ^ \hat{G^{'}_1} G1′^ 所以需要把这些重新收集起来用于优化 θ 2 → θ 3 \theta_2\rightarrow\theta_3 θ2→θ3。
On Policy v.s. Off Policy
- 上面提到的这些训练方法,被训练的 actor 和与环境进行交互的 actor 是同一个 actor ,这种训练的方式叫做
On Policy的方法 - 如果被训练的 actor 和与环境进行交互的 actor 不是同一个 actor 就叫做
Off Policy的方法

Value-based
- value-based 的方法是训练一个 V π V^{\pi} Vπ 这个东西不直接指导 agent 下一步要采取什么 action,他的作用是:给定一个当前环境的状态 s s s 给出一个评估值 v v v,这个评估值表示的是 agent 如果继续玩下去在游戏结束的时候能够获得的预测值
- 举个具体的例子:
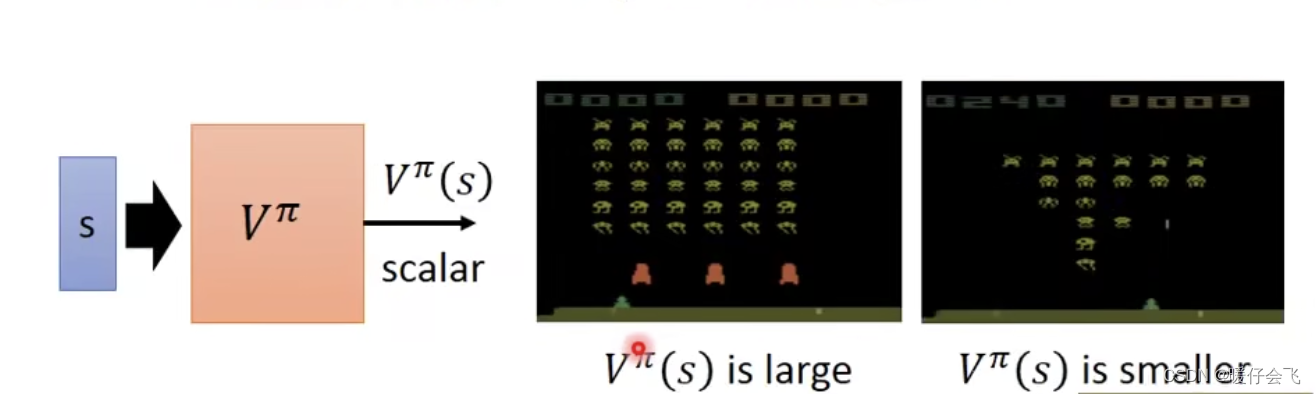
- 第一个游戏图像中的
alien还有很多并且屏障(粉红色的三坨东西)还是满的,所以游戏不太可能在短期内结束,而击杀alien又可以获得reward,那么给定这个 s s s, V π V^\pi Vπ 就会认为:按照当前的情况来看,当游戏结束的时候得到的奖励的值可以比较大( V π ( s ) V^\pi(s) Vπ(s)) 比较大,但是第二个图alien就很稀疏,并且屏障也都已经被 alien 给打没了,所以他的对应的 V π ( s ) V^\pi(s) Vπ(s) 就比较小
- 第一个游戏图像中的


