【数据结构】八大排序:直接插入排序,希尔排序,直接选择排序,堆排序,冒泡排序,快速排序,归并排序,计数排序详细教学_数据结构直接选择排序
赞
踩
一.插入排序
1.直接插入排序
动图演示

图片演示:
- 每次将数据插入到有序的序列,因为第一个数可以视为有序,所以直接将第二个数插入

- 之后再将第三个数与前两个数排序

- 以此类推

- 当我们将最后一位数字插入后,整组数据就有序了

- 代码如下
//直接插入排序 void InsertSort(int* a, int n) { //每次循环都会插入一个新数据 for (int i = 0; i < n - 1; i++) { int end = i;//end为被插入数组的最后一位的下标 int tmp = a[end + 1];//tmp用来保存要插入的数据 while (end >= 0) { //如果数字大于要插入的数据就要往后移一位 if (a[end] > tmp) { a[end + 1] = a[end]; end--; } //如果数字小于要插入的数据就要跳出循环 else { break; } } //将数据插如到end下标的后一位 a[end + 1] = tmp; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
排序特性
1.时间复杂度 O(n2)
最好情况:当序列本身有序时,每次插入数据都是直接插入,只需遍历一次数据,时间复杂度O(n)。
最坏情况:当每次插入新数据时都要遍历一次被插入的序列,时间复杂度为O(n2)。2.空间复杂度:O(1)
空间复杂度为常数值,所以为O(1)。
3.稳定性:稳定
遇到相同的数据直接插入到相同数据后面,不会改变相同数据的前后位置。
2.希尔排序
动图演示

1.希尔排序是直接插入排序的优化。
2.希尔排序分为两部分1.预排序2.直接插入排序
3.希尔排序通过预排序先将序列中的数据进行较大幅移动,让大数字往后移,小数字往前移。这样最后的直接插入排序部分就避免了当插入新数据时会出现遍历较多数据的情况
- 先设定一个gap,gap有两层含义,第一层为每组数据的间隔,第二层为要组数的个数。
- 当gap不为1时就是
预排序,当gap为1时就是直接插入排序。- 预排序时对每组序列运用
直接插入排序的逻辑进行排序
假设gap=5
图片演示:

-
缩小gap

-
当gap变为1时,就是
直接插入排序

-
代码如下
//希尔排序 void ShellSort(int* a, int n) { int gap = n; while (gap > 1) { gap /= 2;//每次缩小gap,当gap为1时就为直接插入排序 for (int i = 0; i < n - gap; i++) { int end = i; int tmp = a[end + gap]; while (end >= 0) { if (a[end] > tmp) { a[end + gap] = a[end]; end -= gap; } else { break; } } a[end + gap] = tmp; } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
排序特性
1.时间复杂度 O(n1.3)
希尔排序的时间复杂度与gap的大小选择有关,目前还无法准确推算出希尔排序的时间复杂度,只能大概推算出为O(n1.3)。
2.空间复杂度:O(1)
空间复杂度为常数值,所以为O(1)。
3.稳定性:不稳定
在预排序阶段有可能改变相同数值的前后位置,所以不稳定
二.选择排序
1.直接选择排序
基本思想:每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
动图演示:

图片演示:
- 第一次遍历数组找出最大值和最小值,将最大值和最小值和第1位和倒数第1位交换
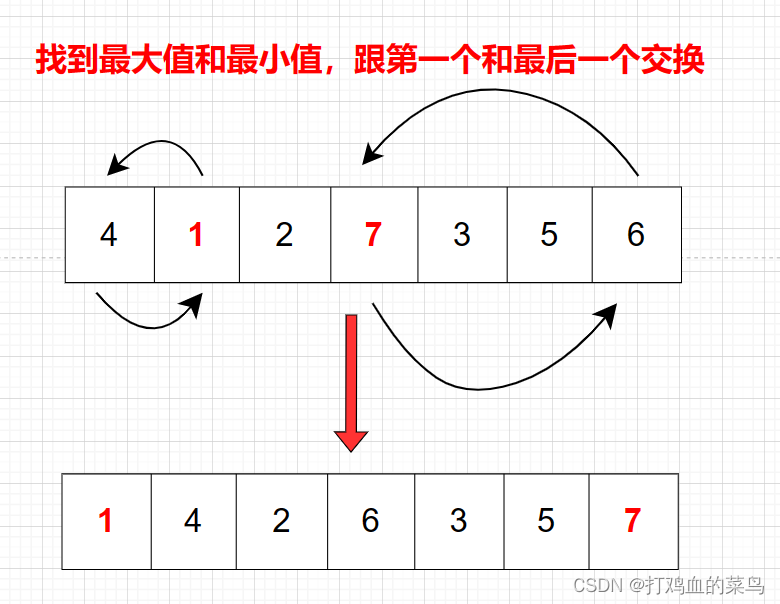
- 第二次遍历数组,找出最大值和最小值,将最大值和最小值和第二位和倒数第二位交换,之后的以此类推

- 代码如下:
//交换函数 void Swap(int* p1, int* p2) { int tmp = *p1; *p1 = *p2; *p2 = tmp; } //直接选择排序 void SelectSort(int* a, int n) { int begin = 0; int end = n - 1; while (begin < end) { int mini = begin; int maxi = begin; for (int i = begin + 1; i <= end; i++) { if (a[mini] > a[i]) { mini = i;//找出最小值的下标 } if (a[maxi] < a[i]) { maxi = i;//找出最大值的下标 } } Swap(&a[begin], &a[mini]); //如果最大值下标在第一位,那么最小值和第一位交换完之后要将maxi赋值给最大值的下标 if (maxi == begin) { maxi = mini;//最大值的下标和mini位置 } Swap(&a[end], &a[maxi]); begin++; end--; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
排序特性
1.时间复杂度 O(n2)
直接选择排序每次都要遍历大量数据
2.空间复杂度:O(1)
空间复杂度为常数值,所以为O(1)。
3.稳定性:不稳定
如果序列两端中有和其他位置相同的值,那么交换时有可能会改变相同值的前后位置,比如
[4,5,6,4,2,8,3] 当2和4交换后,两个4的前后位置就发生了改变,所以不稳定。
2.堆排序
动图演示:
 图片来源于网络,侵删
图片来源于网络,侵删
堆排序是指利用堆这种数据结构所设计的一种排序算法,这里我们以升序为例
堆排序分为两步:1.建堆 2.利用堆进行排序
我们先来看第一步:建堆
-
对于一个数组我们可以将其看成一个
完全二叉树。

-
因为我们要排升序,所以我们需要将这颗树改为
大根堆。大根堆就是每个节点的值都大于或等于其子节点的值。要将树改为大根堆可以用向下调整,并且从最后一个节点的父亲开始。

我们再来看第二步:利用堆进行排序
- 将
堆顶的元素和最后一位进行交换,这样最大的数就跑到了最后一位,然后通过对堆顶向下调整保持剩下元素为大堆

- 代码如下:
//交换函数 void Swap(int* p1, int* p2) { int tmp = *p1; *p1 = *p2; *p2 = tmp; } //向下调整函数 void AdjustDown(int* a, int n, int parent)//parent为要向下调整元素的下标 { int child = parent * 2 + 1;//先设定child为左孩子节点 while (child < n) { //如果右孩子节点比左孩子节点大,则将child改为右孩子 if (child + 1 < n && a[child + 1] > a[child]) { ++child; } // 如果孩子节点大于父亲节点,则和父亲交换 if (a[child] > a[parent]) { Swap(&a[child], &a[parent]); parent = child; child = parent * 2 + 1; } // 如果孩子节点小于父亲节点,则向下调整结束 else { break; } } } //堆排序 O(N*logN) void HeapSort(int* a, int n) { //第一步:先建堆,因为排升序,所以建大根堆。O(n) for (int i = (n - 1 - 1) / 2; i >= 0; --i) { AdjustDown(a, n, i); } //第二步:利用堆进行排序。O(N*logN) int end = n - 1; while (end > 0) { Swap
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55




