- 1UE4.27 编译及打包HTML5相关资料_ue4开发html5 ue和前端通信
- 2大数据开发学习路线_大数据开发工程师的发展路径有哪些
- 3武汉星起航:挂牌上海股权中心,资本赋能共绘跨境电商繁荣新图景
- 4pandas中drop_duplicates函数的用法
- 5nginx屏蔽ip_nginx禁止ip访问的伪静态
- 6数组删除方法_删除数组
- 7Android自定义控件之自定义组合控件_android 自定义控件 merge
- 8第十四届蓝桥杯JavaB组省赛真题 - 蜗牛_蓝桥杯第十四届javab组
- 9〔008〕Stable Diffusion 之 ControlNet 篇_controlnet的最新版本
- 10Rabbitmq 优先队列_rabbitmq优先级队列原理
数据结构——搜索二叉树
赞
踩
前言:
本章我们将认识一种新的二叉树——搜索二叉树。这棵树有个神奇的功能就是会对数据自动排序且有着非常高的查找效率。搜索二叉树作为set、map的基础结构,同样又是接下来将要学到的AVL树以及红黑树的实现基础非常值得我们去深入学习~
一. 概念
叉搜索树本质上也是一种二叉树,只不过多了一个约束规则——
若一棵二叉树不为空,则:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为搜索二叉树
所以构建一个搜索二叉树,只需要在插入结点时满足约束规则即可。
二. 二叉搜索树的操作
与二叉树相同,二叉搜索树由一个个结点链接而成。每个结点包含三个成员——
template <class K>
struct BSTreeNode
{
BSTreeNode<K>* _left; //左孩子
BSTreeNode<K>* _right; //右孩子
K _key; //键值
BSTreeNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{}
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
所以再定义出BSTNode(Binary Search Tree简写)结构体——
template <class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
// 成员函数的实现
// 插入、删除、查找...
private:
Node* _root = nullptr;
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
接着就是各种成员函数的实现了
1.查找
搜索二叉树的查找比较简单而且更容易帮助我们理解搜索二叉树的性质,所以先从查找入手。
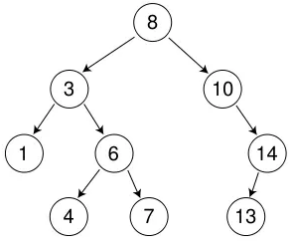
以上图为例,倘若我们要查找 7,具体的思路是这样的——
- 7 < 8,因此去 8 的左子树去查找
- 7 > 3,因此去 3 的右子树去查找
- 7 > 6,因此去 6 的右子树去查找
- 7 = 7,找到了,返回
true
于是我们试着着手实现一个Find函数
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key) // 大于则去右子树查找
cur = cur->_right;
else if (cur->_key > key) // 小于则去左子树查找
cur = cur->_left;
else
return true; // 找到返回true
}
return false; // 未找到返回false
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
2.插入
理解了如何查找,插入也就非常简单。
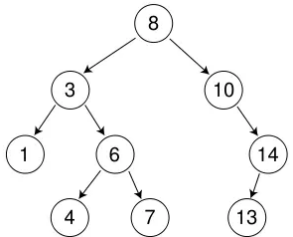
还是以此图为例,倘若我们要插入 9 ,具体步骤为——
- 首先确定
cur的位置,并随时更新parent - 最终,
cur走到10的左节点的位置,即cur = nullptr,循环结束 - 此时
patent = Node*(10) - 最后一步,
new一个结Node*(key)并赋值给parent->_left即可。
bool Insert(const K& key) { // 如果是第一次插入,直接new一个新结点给_root if (_root == nullptr) { _root = new Node(key); return true; } Node* cur = _root; // cur用来定位插入的位置 Node* parent = cur; // 记录parent的父亲 while (cur) { if (cur->_key < key) { parent = cur; cur = cur->_right; } else if(cur->_key > key) { parent = cur; cur = cur->_left; } else { return false; } } // 插入 cur = new Node(key); // 插入时依旧要进行判断 if (parent->_key < key) parent->_right = cur; else parent->_left = cur; return true; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
3.删除(重点)
二叉搜索树的删除是最精华的部分。对与叶子节点,例如4、7、13,删除非常简单,只需将自身的位置替换为nullptr即可。
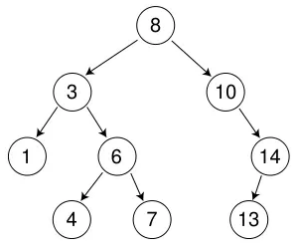
如果要删除14或者10,也是比较简单的,因为10的左右子树只有一方为nullptr(10的左子树为空),所以只需要载删除的时候让父结点接管自己不为空的子树即可。
倘若要删除6或者3,由于它们的左右子树都不为空,删除时无法将两个子树都交给父结点,情况就较为复杂。
所以此种情况,我们只能想办法请一个人来接替自己的位置,但是并不是谁来都能胜任这个位置的。这个接替者必须满足二叉搜索树的条件——左子树都比它小,右子树都比它大。那么这个接替者的人选只能有这两个——
- 左子树的最大(最右)节点
- 或右子树的最小(最左)节点
例如,倘若要删除3,此时有两种做法都可行——
- 用1替换3
- 用7替换3
综上所述,删除操作共分为一下几种情况——
- 左子树为空
- 右子树为空
- 左右子树都不为空
- (左右子树都为空其实可以归并到1或2的情况中)
bool Erase(const K& key) { Node* cur = _root; Node* parent = cur; while (cur) { // 找到值为key的结点 if (cur->_key < key) { parent = cur; cur = cur->_right; } else if (cur->_key > key) { parent = cur; cur = cur->_left; } else // 找到了 { // 删除 if (cur->_left == nullptr) // 1.左子树为空 { if (cur == _root) // 根节点的删除 { _root = cur->_right; return true; } else { if (parent->_left == cur) parent->_left = cur->_right; else parent->_right = cur->_right; delete cur; } } else if (cur->_right == nullptr) // 2.右子树为空 { if (cur == _root) // 根节点的删除 { _root = cur->_left; return true; } else { if (parent->_left == cur) parent->_left = cur->_left; else parent->_right = cur->_left; delete cur; } } else // 左右子树都不为空 { // 找左子树的最大结点 或者 右子树的最小结点 Node* minRight = cur->_right; Node* pminRight = cur; while (minRight->_left) { pminRight = minRight; minRight = minRight->_left; } cur->_key = minRight->_key; // 替换 if (pminRight->_left == minRight) { pminRight->_left = minRight->_right; } else { pminRight->_right = minRight->_right; } delete minRight; } return true; } } return false; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
4.遍历
二叉搜索树的遍历非常简单,就是之前学习过的二叉树的中序遍历。
void InOrder()
{
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << ' ';
_InOrder(root->_right);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
注:由于调用函数时C++封装的特性,需设计两个函数,InOrder接口对外提供,_InOrder不对外提供。
5.拷贝构造与析构
//采用前序遍历拷贝构造 BSTree(const BSTree<K>& t) { _root = _Copy(t._root); } Node* _Copy(Node* root) { if (root ==nullptr) { return nullptr; } Node* CopyRoot = new Node(root->_key); CopyRoot->_left = _Copy(root->_left); CopyRoot->_right = _Copy(root->_right); return CopyRoot; } //采用后序遍历的方式来删除,从下往上删。 void _Destroy(Node*& root) { if (root == nullptr) { return; } _Destroy(root->_left); _Destroy(root->_right); delete root; root = nullptr; } ~BSTree() { _Destroy(_root); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
因为拷贝构造二叉搜索树时要保证树的结构与原来树的结构一致,因此采用前序遍历进行拷贝构造。
但如果写了拷贝构造之后编译器就不会生成默认的构造函数了,因为拷贝构造也属于构造,因此可以利用一下C++11的特性,强制编译器生成一个默认的拷贝构造
//强制编译器生成一个默认的拷贝构造
BSTree() = default;
- 1
- 2
三.二叉搜索树的递归实现
对于搜索二叉树来说,上面实现的非递归版本是比递归版本更优的。此处的递归实现完全属于多余了,但是作为拓展内容看一看也未尝不可。
1.递归查找
bool FindR(const K& key) { return _FindR(_root, key); } bool _FindR(Node* root, const K& key) { if (root == nullptr) return false; if (root->_key == key) return true; if (root->_key > key) _FindR(root->_left, key); else _FindR(root->_right, key); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
2.递归插入
bool InsertR(const K& key) { return _EraseR(_root, key); } bool _InsertR(Node*& root, const K& key) { if (root == nullptr) { root = new Node(key); return true; } if (root->_key < key) return _InsertR(root->_right, key); else if (root->_key > key) return _InsertR(root->_left, key); else return false; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
3.递归删除
bool EraseR(const K& key) { return _EraseR(_root, key); } bool _EraseR(Node*& root, const K& key) { if (root == nullptr)return false; if (root->_key < key) return _EraseR(root->_right, key); else if(root->_key>key) return _EraseR(root->_left, key); else { Node* del = root; //1.右为空 if (root->_right == nullptr) root = root->_left; //2.左为空 else if (root->_left) root = root->_right; //3.左右都不为空 else { //找左子树最大节点交换 Node* maxleft = root->_left; while (maxleft->_right) maxleft = maxleft->_right; //找到后先交换要删除的值与左子树最大节点的值 swap(root->_key, maxleft->_key); //再递归到左子树中去删除 return _EraseR(root->_left, key); } delete del; return true; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
四.二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二
叉搜索树的深度的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:

- 最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为: l o g 2 N log_2 N log2N
- 最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为: N 2 \frac{N}{2} 2N
如果退化成单支树,二叉搜索树的性能就失去了。那能否进行改进,不论按照什么次序插 入关键码,二叉搜索树的性能都能达到最优? 那么我们后续章节学习的AVL树和红黑树就可以上场了。
五.二叉树搜索的应用
K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。
比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:- 以词库中所有单词集合中的每个单词作为
key,构建一棵二叉搜索树 - 在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
- 以词库中所有单词集合中的每个单词作为
KV模型:每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。该种方式在现实生活中非常常见:- 比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文
<word, chinese>就构成一种键值对 - 再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出现次数就是
<word, count>就构成一种键值对
- 比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文
六.源码
namespace dianxia { template <class K> struct BSTreeNode { BSTreeNode<K>* _left; BSTreeNode<K>* _right; K _key; BSTreeNode(const K& key) :_left(nullptr) , _right(nullptr) , _key(key) {} }; template <class K> class BSTree { typedef BSTreeNode<K> Node; public: //强制编译器生成构造函数 BSTree() = default; //拷贝构造 BSTree(const BSTree<K>& t) { _root = Copy(t._root); } //赋值重载 BSTree<k>& operator=(BSTree<K> t) { swap(_root, t._root); return *this; } ~BSTree() { Destroy(_root); } //插入节点 bool Insert(const K& key) { //直接插入根 if (_root == nullptr) { _root = new Node(key); return true; } Node* parent = nullptr; Node* cur = _root; while (cur) { if (cur->_key < key) { parent = cur; cur = cur->_right; } else if (cur->_key > key) { parent = cur; cur = cur->_left; } else { returen false; } } cur = new Node(key); if (parent->_key < key) { parent->_right = cur; } else { parent->_left = cur; } return true; } bool Find(const K& key) { Node* cur = _root; while (cur) { if (cur->_key < key) { cur = cur->_right; } else if (cur->_key > key) { cur = cur->_left; } else { returen true; } } return false; } bool Erase(const K& key) { Node* parent = nullptr; Node* cur = _root; while (cur) { if (cur->_key < key) { parent = cur; cur = cur->_right; } else if (cur->_key > key) { parent = cur; cur = cur->_left; } else { //1.左为空 if (cur->_left == nullptr) { if (cur == _root) { _root = cur->_right; } else { if (parent->_left == cur) { parent->_left = cur->_right; } else { parent->_right == cur->_right; } } delete cur; } //2.右为空 else if (cur->_right == nullptr) { if (cur == _root) { _root = cur->_left; } else { if (parent->_left == cur) { parent->_left = cur->_left; } else { parent->_right == cur->_left; } } delete cur; } //3.左右都不为空,找右树最小节点或左树最大节点替代cur else { Node* pminRight = cur; Node* minRight = cur->_right; while (minRight->_left) { pminRight = minRight; minRight = minRight->_left; } cur->_key = minRight->_key; if (pminRight->_left == minRight) { pminRight->_left = minRight->_right; } else { pminRight->_right = minRight->_right; } delete minRight } return true; } } return false; } //递归版 bool FindR(const K& key) { return _FindR(_root, key); } bool InsertR(const K& key) { return _InsertR(_root, key); } bool Erase(const K& key) { return _Erase(_root, key); } bool Insorder() { _Insorder(_root); cout << endl; } protected: Node* Copy(Node* root) { if (root == nullptr) return nullptr; Node* newRoot = new Node(root->_key); newRoot->_left = Copy(root->_left); newRoot->_right = Copy(root->_right); return newRoot; } void Destroy(Node*& root) { if (root == nullptr) return; Destroy(root->_left); Destroy(root->_right); delete root; root = nullptr; } bool _FindR(Node* root, const K& key) { if (root == nullptr) return false; if (root->_key == key) return true; if (root->_key < key) return _FindR(root->_right, key); else return _FindR(root->_left, key); } bool _InsertR(Node*& root, const K& key) { if (root == nullptr) { root = new Node(key); return true; } if (root->_key < key) { return _InsertR(root->_right, key); } else if (root->_key > key) { return _InsertR(root->_left, key); } else { return false; } } bool _EraseR(Node*& root, const K& key) { if (root == nullptr)return false; if (root->_key < key) return _EraseR(root->_right, key); else if(root->_key>key) return _EraseR(root->_left, key); else { Node* del = root; //1.右为空 if (root->_right == nullptr) root = root->_left; //2.左为空 else if (root->_left) root = root->_right; //3.左右都不为空 else { //找左子树最大节点交换 Node* maxleft = root->_left; while (maxleft->_right) maxleft = maxleft->_right; //找到后先交换要删除的值与左子树最大节点的值 swap(root->_key, maxleft->_key); //再递归到左子树中去删除 return _EraseR(root->_left, key); } delete del; return true; } } private: Node* _root; }; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
- 225
- 226
- 227
- 228
- 229
- 230
- 231
- 232
- 233
- 234
- 235
- 236
- 237
- 238
- 239
- 240
- 241
- 242
- 243
- 244
- 245
- 246
- 247
- 248
- 249
- 250
- 251
- 252
- 253
- 254
- 255
- 256
- 257
- 258
- 259
- 260
- 261
- 262
- 263
- 264
- 265
- 266
- 267
- 268
- 269
- 270
- 271
- 272
- 273
- 274
- 275
- 276
- 277
- 278
- 279
- 280
- 281
- 282
- 283
- 284
- 285
- 286
- 287
- 288
- 289
- 290
- 291
- 292
- 293
- 294
- 295
- 296
- 297
- 298
本文到此结束,码文不易,还请多多支持!!!



