回溯法解决n皇后问题（迭代版）_求解n皇后问题迭代

n皇后问题的关键在于judge函数，判断当前的情况是否合法

        1.x[i]==x[k]说明有两个皇后处于同一列，不符合
        2.x[k]-x[i]==k-i：
        由于k-i是固定的，假设k=3,i=2,那么k-i=1,
        如果x[k]-x[i]=1, 说明第k个皇后在第i个皇后右下角
        如果x[k]-x[i]=-1,说明第k个皇后在第i个皇后左下角
        其他情况如k=5,i=3以此类推
        不用考虑第k个皇后在第i个皇后左上角或者右上角的情况
        因为for循环从小到大循环，保证了k是i后面的数 

bool judge(int k)
{
	if(k==1) return true;
	else
	{	
		if(x[k]<=0) return false;
//		1.x[i]==x[k]说明有两个皇后处于同一列，不符合
//		2.x[k]-x[i]==k-i：
//		由于k-i是固定的，假设k=3,i=2,那么k-i=1,
//		如果x[k]-x[i]=1, 说明第k个皇后在第i个皇后右下角
//		如果x[k]-x[i]=-1,说明第k个皇后在第i个皇后左下角
//		其他情况如k=5,i=3以此类推
//		不用考虑第k个皇后在第i个皇后左上角或者右上角的情况
//		因为for循环从小到大循环，保证了k是i后面的数 
		for(int i=1;i<k;i++)
			if(x[i]==x[k]||x[k]-x[i]==k-i||x[k]-x[i]==i-k)
				return false;
		return true;
	}
}

这个迭代版本的算法模仿了递归版本的算法，因此每一次回退都要”恢复现场“

		//恢复现场
		x[k]=0;
		k=k-1; 

完整代码

#include<iostream>
using namespace std;
const int N=1010;
int x[N];//x[i]表示第i个点放在第几列 
int n,cnt;
bool judge(int k)
{
	if(k==1) return true;
	else
	{	
		if(x[k]<=0) return false;
//		1.x[i]==x[k]说明有两个皇后处于同一列，不符合
//		2.x[k]-x[i]==k-i：
//		由于k-i是固定的，假设k=3,i=2,那么k-i=1,
//		如果x[k]-x[i]=1, 说明第k个皇后在第i个皇后右下角
//		如果x[k]-x[i]=-1,说明第k个皇后在第i个皇后左下角
//		其他情况如k=5,i=3以此类推
//		不用考虑第k个皇后在第i个皇后左上角或者右上角的情况
//		因为for循环从小到大循环，保证了k是i后面的数 
		for(int i=1;i<k;i++)
			if(x[i]==x[k]||x[k]-x[i]==k-i||x[k]-x[i]==i-k)
				return false;
		return true;
	}
}
void solve(int k)
{
	while(k>=1)
	{
		while(x[k]<=n-1)
		{
			x[k]=x[k]+1;
//			printf("k=%d,x[k]=%d\n",k,x[k]);
			//判断当前位置是否合法
			if(judge(k))
			{	
				if(k!=n)
					k++;
				else if(k==n)
				{	
					cnt++;
					printf("--------找到合法解决方案！--------\n");
					for(int i=1;i<=n;i++)
						printf("%d ",x[i]);
					printf("\n");
				}
			}
 
		}
		//恢复现场
		x[k]=0;
		k=k-1; 
	}
}
int main()
{
	cin>>n;
	
	for(int i=1;i<=n;i++)//虽然全局变量初始化过了，这里显式初始化 
		x[i]=0;
		
	solve(1);
	
	printf("共有%d种解决方案!\n",cnt);
	
	return 0;
}

运行结果（n=8)：

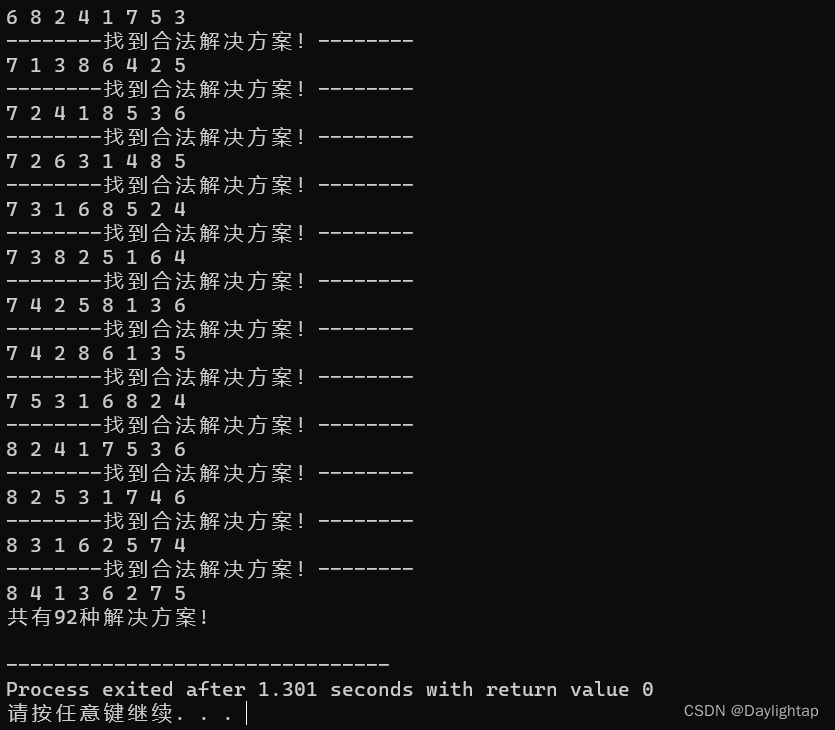
标准答案：

对于N从1到8的N皇后问题，以下是每个N值对应的解决方案数量：

• N=1: 1种解决方案
• N=2: 0种解决方案
• N=3: 0种解决方案
• N=4: 2种解决方案
• N=5: 10种解决方案
• N=6: 4种解决方案
• N=7: 40种解决方案
• N=8: 92种解决方案

对照标准答案，我们可以知道这个算法是正确的