机器学习(四）：决策树绘画（基础篇）_决策树绘图代码

在前面的章节中，我们已经学过了ID3树，C4.5树和CART树的构造。如果还没有了解过这三棵决策树的话可以点击下方链接：

相关的决策树文章：

• 机器学习（四）ID3决策树
• 机器学习（四）C4.5决策树
• 机器学习（四）CART分类树
• 机器学习（四）CART回归树
• 机器学习（四）剪枝技术

下面我们来看看在前面所生成的决策树的模样。

决策树的文字格式

决策树没有绘图之前是由一个多重字典组成，如图：

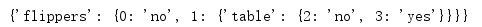
这是我们生成的决策树的文字格式，如今，我们要将其转到图像化。

决策树绘图代码

import matplotlib.pylab as plt

#用来正常显示中文
plt.rcParams['font.sans-serif']=['SimHei']
#用来正常显示负号
plt.rcParams['axes.unicode_minus']=False

def getNumLeafs(myTree):
    #初始化树的叶子节点的个数
    numLeafs = 0
    #myTree.keys()获取树的非叶子节点’no surfacing'和‘flippers’
    #list(mytree.keys()[0]获取第一个键名‘no surfacing’
    firstStr = list(myTree.keys())[0]
    #通过键名获取与之对应的值，即{0:'no',1:{'flippers':{0:'no,1:'yes'}}}
    secondDict = myTree[firstStr]
    #遍历树，secondDict.keys()获取所有的键
    for key in secondDict.keys():
        #判断键是否为字典，键名1和其值就组成了一个字典，如果是字典则通过递归继续遍历，寻找叶子节点
        if type(secondDict[key]).__name__=='dict':
            numLeafs += getNumLeafs(secondDict[key])
        #如果不是字典，则叶子节点的数目就加1
        else:
            numLeafs += 1
        #返回叶子节点的数目
    return numLeafs

def getTreeDepth(mytree):
    #初始化树的深度
    maxDepth = 0
    #获取树的第一个键名
    firstStr = list(mytree.keys())[0]
    #获取键名所对应的值
    secondDict = mytree[firstStr]
    #遍历树
    for key in secondDict.keys():
        #如果获取的键是字典，树的深度加一
        if type(secondDict[key]).__name__=='dict':
            thisDepth = 1+ getTreeDepth(secondDict[key])
        else:
            thisDepth = 1
        #去深度最大值
        if thisDepth > maxDepth : maxDepth = thisDepth
    #返回树的深度
    return maxDepth

#设置画节点用的盒子的样式
decisionNode = dict(boxstyle = 'sawtooth', fc='0.8')
leafNode = dict(boxstyle = 'round4', fc = '0.8')

#设置画箭头的样式
arrow_args = dict(arrowstyle="<-")
#绘图相关参数的设置
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    #annotate函数是为绘制图上指定的数据点xy添加一个nodeTxt注释
    #nodeTxt是给数据点xy添加一个注释，xy为数据点的开始绘制的坐标,位于节点的中间位置
    #xycoords设置指定点xy的坐标类型，xytext为注释的中间点坐标，textcoords设置注释点坐标样式
    #bbox设置装注释盒子的样式,arrowprops设置箭头的样式
    '''
        figure points:表示坐标原点在图的左下角的数据点
        figure pixels:表示坐标原点在图的左下角的像素点
        figure fraction：此时取值是小数，范围是([0,1],[0,1]),在图的左下角时xy是（0,0），最右上角是(1,1)
        其他位置是按相对图的宽高的比例取最小值
        axes points : 表示坐标原点在图中坐标的左下角的数据点
        axes pixels : 表示坐标原点在图中坐标的左下角的像素点
        axes fraction : 与figure fraction类似，只不过相对于图的位置改成是相对于坐标轴的位置
    '''
    createPlot.ax1.annotate(nodeTxt, xy=parentPt,
                            xycoords='axes fraction', xytext=centerPt, textcoords='axes fraction',
                            va='center', ha='center', bbox=nodeType, arrowprops=arrow_args)

#绘制线中间的文字（0和1）的绘制
def plotMidText(cntrPt, parentPt, txtString):
    xMid = (parentPt[0] - cntrPt[0])/2.0 + cntrPt[0]
    yMid = (parentPt[1] - cntrPt[1])/2.0 + cntrPt[1]
    createPlot.ax1.text(xMid, yMid, txtString)

#绘制树
def plotTree(myTree, parentPt, nodeTxt):
    #获取树的叶子节点
    numLeafs = getNumLeafs(myTree)
    #获取树的深度
    depth = getTreeDepth(myTree)
    #firstStr = mytree.keys()[0]
    #获取第一个键名
    firstStr = list(myTree.keys())[0]
    # 计算子节点的坐标
    cntrPt = (plotTree.xoff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yoff)
    # 绘制线上的文字
    plotMidText(cntrPt, parentPt, nodeTxt)
    # 绘制节点
    plotNode(firstStr, cntrPt, parentPt, decisionNode)
    # 获取第一个键值
    secondDict = myTree[firstStr]
    # 计算节点y方向上的偏移量，根据树的深度
    plotTree.yoff = plotTree.yoff - 1.0 / plotTree.totalD
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            # 递归绘制树
            plotTree(secondDict[key], cntrPt, str(key))
        else:
            # 更新x的偏移量,每个叶子结点x轴方向上的距离为 1/plotTree.totalW
            plotTree.xoff = plotTree.xoff + 1.0 / plotTree.totalW
            # 绘制非叶子节点
            plotNode(secondDict[key], (plotTree.xoff, plotTree.yoff), cntrPt, leafNode)
            # 绘制箭头上的标志
            plotMidText((plotTree.xoff, plotTree.yoff), cntrPt, str(key))
    plotTree.yoff = plotTree.yoff + 1.0 / plotTree.totalD

#绘制决策树，inTree的格式为{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}
def createPlot(inTree):
    #新建一个figure设置背景颜色为白色
    fig = plt.figure(1,facecolor='white')
    #清除figure
    fig.clf()
    axprops = dict(xticks=[],yticks=[])
    #创建一个1行1列1个figure，并把网格里面的第一个figure的Axes实例返回给ax1作为函数createPlot()
    #的属性，这个属性ax1相当于一个全局变量，可以给plotNode函数使用
    createPlot.ax1 = plt.subplot(111,frameon=False,**axprops)
    #获取树的叶子节点
    plotTree.totalW = float(getNumLeafs(inTree))
    #获取树的深度
    plotTree.totalD = float(getTreeDepth(inTree))
    #节点的x轴的偏移量为-1/plotTree.totlaW/2,1为x轴的长度，除以2保证每一个节点的x轴之间的距离为1/plotTree.totlaW*2
    plotTree.xoff = -0.5/plotTree.totalW
    plotTree.yoff = 1.0
    plotTree(inTree,(0.5,1.0),'')
    plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128

绘图代码的使用

将绘图的代码的py文件放置于前面三个文件的同一文件目录下。只需要在三个决策树的代码文件中加入：

import plotTrees   #加在代码头

plotTrees.createPlot(myTree)  #加在代码的尾
1
2
3

结果1：ID3决策树

结果2：C4.5决策树

结果3：CART决策树

成功的画出了三个决策树的图解，是不是感觉自己很棒呢。哈哈。